在这一页
不同的双打
简介
“不同双倍”是比洛克西博里瓦奇赌场常见的一种掷骰子附加赌注。它根据掷骰者在掷出总数为7之前掷出的不同双倍的次数来支付赔付。赔付表如下:
- 6 次双倍赔率为 100 比 1
- 5 次双倍赔率为 15 比 1
- 4 个双倍赔率为 8 比 1
- 3 次双倍赔率 4 比 1
分析
下表显示了所有可能结果的概率及其对回报的贡献。右下角单元格显示庄家优势为 27.92%(哎哟!)。
不同双打回报表
| 双打 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 6 | 100 | 1 | 0.001082 | 0.108225 |
| 5 | 15 | 6 | 0.006494 | 0.097403 |
| 4 | 8 | 21 | 0.022727 | 0.181818 |
| 3 | 4 | 56 | 0.060606 | 0.242424 |
| 2 | -1 | 126 | 0.136364 | -0.136364 |
| 1 | -1 | 252 | 0.272727 | -0.272727 |
| 0 | -1 | 462 | 0.500000 | -0.500000 |
| 全部的 | 924 | 1.000000 | -0.279221 |
代数分析
任何给定双倍的概率为 1/36。因此,任何双倍的概率为 6/36 = 1/6。任何七的概率为 1/6。除了双倍和七之外,我们可以忽略所有掷出的点数。因此,假设有一轮掷出的点数与投注相关,则该轮的概率如下:
- 任意双倍 = 1/2
- 任意七 = 1/2
第一次掷出有效点数 7 的概率是 1/2。因此,出现双倍点数的概率为零。
否则,玩家就会掷出双点。现在我们可以忽略再次掷出双点这一重要事件。两种重要事件的概率现在分别为:
- 任何显著的双倍 = 5/11
- 任意七 = 6/11
此时,玩家掷出7点(一次双倍)的概率为6/11。因此,掷出一次双倍的总体概率为(1/2)*(6/11) = 3/11 = 约27.27%。
否则,玩家就会掷出第二个双倍。现在,我们可以忽略掷出两个不同的双倍作为显著事件。现在,两种显著事件的概率分别为:
- 任何显著的双倍 = 4/10
- 任意七 = 6/10
此时玩家掷出两次双倍点数的概率为 6/10。因此,一次双倍点数的总体概率为 (1/2)*(5/11)*(6/10) = 3/22 = 约 13.6363636%。
否则,玩家就会掷出第三个双数。现在我们可以忽略掷出三个不同的双数作为显著事件。两种显著事件的概率现在分别为:
- 任何显著的双倍 = 3/9
- 任意七 = 6/9
此时玩家掷出两次双倍点数的概率为 6/9。因此,掷出一次双倍点数的总体概率为 (1/2)*(5/11)*(4/10)*(6/9) = 2/33 = 约 6.060606%。
否则,玩家就会掷出第四个双数。现在我们可以忽略掷出四个不同的双数作为显著事件。两种显著事件的概率现在分别为:
- 任何显著的双倍 = 2/8
- 任意七 = 6/8
此时玩家掷出两次双倍点数的概率为 6/8。因此,一次双倍点数的总体概率为 (1/2)*(5/11)*(4/10)*(3/9)*(6/8) = 1/44 = 约 2.272727%。
否则,玩家就会掷出第五个双数。现在我们可以忽略掷出五个不同的双数作为显著事件。两种显著事件的概率现在分别为:
- 任何显著的倍数 = 1/7
- 任意七 = 6/7
此时玩家掷出两次双倍的概率为 6/7。因此,一次双倍的总体概率为 (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(6/7) = 1/154 = 约 0.649351%。
否则,玩家会掷出最后一个剩下的双点。其概率为 (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(1/7) = 1/924 = 约 0.108225%。
现在,我们可以将所有这些放在上面的回报表中。组合数共有 924 种。
积分分析
想象一下,重大事件不再由一次掷骰子来决定,而是被视为一个时间瞬间。假设事件之间的时间间隔具有无记忆性,平均间隔一个单位时间。换句话说,事件之间的时间间隔服从均值为1的指数分布。这对于裁决赌注来说无关紧要,因为事件仍然是一次一个地发生的。
特定双倍事件之间的时间间隔服从指数分布,平均值为 12。之所以使用 12,是因为如果发生重大事件,则有 1/12 的概率是该特定双倍事件。因此,特定双倍事件在 x 个单位时间内未发生的概率为 exp(-x/12)。因此,它发生的概率为 1-exp(-x/12)。
设 x 为投注开始以来的时间单位数。所有双倍出现且未出现七的概率为 (1-exp(-x/12)) 6 × exp(-x/2)。
以在时间 x 掷出 7 来结束此过程,将其乘以 1/2(掷出 7 的概率),得到在时间 x 恰好掷出获胜的概率为 (1/2) ×(1-exp(-x/12)) 6 × exp(-x/2)
要找出所有时间内获胜的概率,请从 1 到无穷大进行积分:
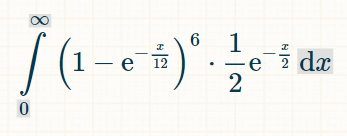
要计算积分,我推荐使用这个积分计算器。在积分栏中输入“(1-exp(-x/12))^6*(1/2)*exp(-x/2)”。对于积分极限,在选项下输入 0 和 ∞。然后点击“开始”。“它将给出下面的积分:
(-(1-e^(-x/12))^12+(60*(1-e^(-x/12))^11)/11-12*(1-e^(-x/12))^10+(40 *(1-e^(-x/12))^9)/3-(15*(1-e^(-x/12))^8)/2+(12*(1-e^(-x/12))^7)/7)/2
但是,我们不需要输入 0。计算器给出的答案是 1/924 = 约 0.001082251082251082。
这是五种不同加倍的积分。结果为 6 是因为有 6 种可能的加倍没有被算出来:
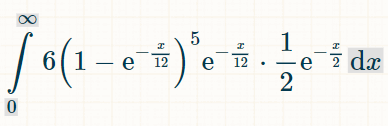
这是在 x 个时间单位内获胜的概率:
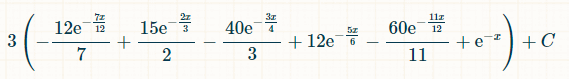
将积分范围设为从 0 到无穷大,则掷出五个不同双数的概率为 1/154。
这是四个不同双精度浮点数的积分。之所以是 15,是因为在 6 个浮点数中,有 4 个浮点数有 6!/(4!*2!) = 15 种可能的组合:
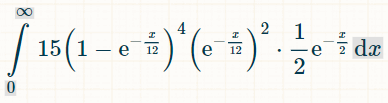
这是在 x 个时间单位内获胜的概率:
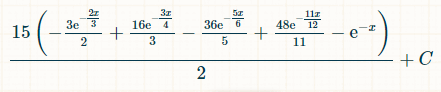
将积分范围设为从 0 到无穷大,则掷出四个不同双精度数的概率为 1/44。
这是三个不同双精度数的积分。之所以是 20,是因为在 6 个双精度数中,有 3 个可能的组合,一共有 6!/(3!*3!) = 20 种:
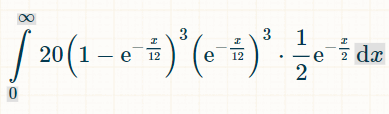
这是在 x 个时间单位内获胜的概率:
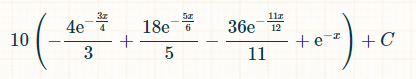
将积分范围设为从 0 到无穷大,则掷出三个不同双精度数的概率为 2/33。



