在这一页
红利掷骰子
简介
奖金掷骰子(Bonus Craps)是掷骰子游戏中的一组三种附加赌注。具体如下:
- 小——如果投掷者掷出总数为 2 至 6 之间的所有点数,然后才掷出总数为 7,则获胜。获胜赔率通常为 30 比 1。
- 高点数 (Tall) — 如果投掷者掷出总数为 8 至 12 之间的所有点数,然后才掷出总数为 7,则获胜。获胜赔率通常为 30 比 1。
- 全部 — 如果投掷者在掷出总数 7 之前掷出 2 到 12 之间的所有数字(除 7 外),则获胜。获胜赔率通常为 150 比 1。
2021 年,我开始在威尼斯人看到这种名为“Diceology”的赌注。
分析
下表显示了我对小注和大注的分析,获胜赔率为 30 比 1。右下角单元格显示庄家优势为 18.30%。
小而高
| 事件 | 支付 | 可能性 | 返回 |
|---|---|---|---|
| 赢 | 三十 | 0.026354 | 0.790617 |
| 损失 | -1 | 0.973646 | -0.973646 |
| 全部的 | 1.000000 | -0.183029 |
过去,一些赌桌在小型和大型赌桌上的赔率高达1比34。如今这些赔率更高,赌场优势高达7.76%。
下表显示了我对“全部下注”的分析,获胜赔率为 150 比 1。右下角单元格显示庄家优势为 20.61%。
全部
| 事件 | 支付 | 可能性 | 返回 |
|---|---|---|---|
| 赢 | 150 | 0.005258 | 0.788655 |
| 损失 | -1 | 0.994742 | -0.994742 |
| 全部的 | 1.000000 | -0.206087 |
我见过“全注”的其他赔率,包括1比155和1比175。记得在赔率中减去1,才能将赔率从“一比一”转换为“一比一”。下表显示了赔率在150到175之间,且能被5整除的赔率的赌场优势。
All Bet 的庄家优势总结
| 支付 | 庄家优势 |
|---|---|
| 150 | 20.61% |
| 155 | 17.98% |
| 160 | 15.35% |
| 165 | 12.72% |
| 170 | 10.09% |
| 175 | 7.46% |
方法论
我从三个方面分析了 Bonus Craps,如下所示:
- 模拟——这可能是最简单的方法。然而,对于像我这样的数学纯粹主义者来说,模拟总是无法带来足够的智力满足。
- 马尔可夫链——这种方法繁琐且耗时。对于“小”和“高”模型,它需要一个 6x6 的转移矩阵,而对于“全”模型,则需要一个 12x12 的转移矩阵。
- 积分微积分——使用积分计算器,这种方法非常简单。我将在下文中更深入地解释。
想象一下,重大事件不再由一次掷骰子决定,而是被视为一个时间瞬间。假设事件之间的时间间隔具有无记忆性,平均间隔为一个时间单位。换句话说,事件之间的时间间隔服从均值为1的指数分布。这对于判断赌注而言无关紧要,因为事件仍然是一次一个地发生的。
以下是在 x 个时间单位内任何给定总数至少未滚动一次的概率:
- 2 或 12:exp(-x/36)
- 3 或 11:exp(-x/18)
- 4 或 10:exp(-x/12)
- 5 或 9:exp(-x/9)
- 6 或 8:exp(-5x/36)
- 7:exp(-x/6)
我们先来看看小注。大注的赔率和小注完全一样。
在 x 个时间单位内,掷出 2、3、4、5 和 6 而未掷出 7 的概率为: (1-exp(-x/36))*(1-exp(-x/18))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-5x/36))*exp(-x/6) 在时间 x 处,玩家掷出 7,之前掷出的总数为 2 到 6,则该玩家的概率为:
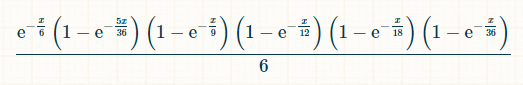
对于积分,我使用了这个积分计算器。
由于中奖号码 7 随时可能出现,中奖概率就是该概率对 x 从 0 到无穷大的积分。我们不需要知道,但在代入积分极限之前,积分是(-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^ (-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(- (7*x)/18))/7+(12*e^(-(5*x)/12))/5+(9*e^(-(4*x)/9))/4-(36*e^ (-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6。
代入积分极限,答案是 20049 / 760760 = 约 0.02635390924864609。
接下来我们看一下全注。
在 x 个时间单位内,掷出 2、3、4、5、6、8、9、10、11 和 12 而未掷出 7 的概率为: (1-exp(-x/36)) 2 *(1-exp(-x/16)) 2 *(1-exp(-x/12)) 2 *(1-exp(-x/9)) 2 *(1-exp(-5x/36)) 2 *exp(-x/6) 在时间 x 处,玩家掷出 7,之前掷出的总数为 2 到 6,则该玩家的概率为:
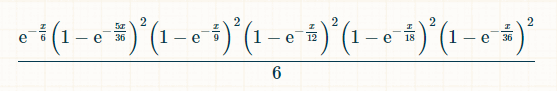
由于中奖数字 7 随时可能出现,中奖概率就是该概率对 x 从 0 到无穷大的积分。我们不需要知道这个值,但在带入积分极限之前,积分等于 (-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5*x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/1) 8))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10* e^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+ (54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^( -(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9) )/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e ^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6。
代入积分极限,答案是 126538525259 / 24067258815600 = 0.0052577040961964420049。



