概率 - 谜题
我对掷骰子概率的具体信息很感兴趣。如果你有6个骰子,一次全部掷出,那么掷出全1的概率是46,656分之一。我的问题是,掷出1到5个1的概率是多少。我非常想知道应该用什么公式来计算这类问题。
y 个骰子中掷出 x 个 1 的概率为 combin(y,x)*(1/6) x *(5/6) yx 。请参阅我关于扑克概率的部分,了解 combin(x,y) 函数的解释。例如,掷出 4 个 1 的概率为 combin(6,4)*(1/6) 4 *(5/6) 2 = 0.803755%。
六个骰子中“1”的个数
| 一 | 可能性 |
|---|---|
| 0 | 0.3348980 |
| 1 | 0.4018776 |
| 2 | 0.2009388 |
| 3 | 0.0535837 |
| 4 | 0.0080376 |
| 5 | 0.0006430 |
| 6 | 0.0000214 |
| 全部的 | 1.0000000 |
八名高尔夫球手来到一个新球场。球童主管随机将8个球袋放在四辆球车上。球手们将8个带标记的高尔夫球放入一顶帽子中。球被抛向空中。距离最近的两个球是同伴的球袋。在所有情况下,同伴的球袋都已经放在同一辆球车上。在抛球之前,这些球袋已经正确配对的概率是多少?
组合数的公式答案为:combin(8,2)*combin(6,2)*combin(4,2)/fact(4) = 25*15*6/24 = 105。另一种计算组合数的方法是随机选择一名高尔夫球手。有7个人可以与他配对。然后从剩下的6个人中随机选择另一名高尔夫球手。有5个人可以与他配对。然后从剩下的4个人中随机选择另一名高尔夫球手。有3个人可以与他配对。所以组合数为7*5*3 = 105。因此答案为1/105。
一个朋友把这个发给了我,我想知道是否有一个公式可以解释这个是如何工作的。
这些读心数字谜题之所以奏效,往往是因为一个有趣的数学奇点。如果一个数字的各位数字之和能被9整除,那么这个数字本身也能被9整除。我们来试试拉斯维加斯Tropicana酒店的电话号码(702-739-2222)。各位数字之和是7+0+2+7+3+9+2+2+2+2=36。36能被9整除,所以702739222也一定能被9整除。这里有一个证明。
- 令 n 为任意整数。将 n 表示为 d 0 *1 + d 1 *10 + d 2 *100+ d 3 *1000+ ... + d n *10 n ,其中 d n是第一位数字,d n-1是第二位数字,依此类推。
- n = [d 0 + d 1 + d 2 + ... + d n ] + [d 1 *9 + d 2 *99+ d 3 *999+ ...+ d n *999...9(一个包含 n 个 9 的数字)]
- n = [d 0 + d 1 + d 2 + ... + d n ] + 9*[d 1 *1 + d 2 *11+ d 3 *111+ ... d n *111...1(一个有 n 个 1 的数字)]
- 9*任何整数都能被 9 整除。因此,如果 d 0 + d 2 + d 2 + ... + d n (或数字之和)能被 9 整除,那么整个数字一定能被 9 整除。
现在我们已经有了证明,可以来看看这个魔术了。题目要求你选一个数字。然后重新排列数字,得到第二个数字。最后用较大的数字减去较小的数字。
答案总是数字之和能被 9 整除。为什么?因为原数中的每个数字都会出现在另一个数的某个位置。每次处理一组数字,将其他所有数字都变为零,我们可以将每组数字归结为 +/- n*[10 x - 10 y ](其中 x>=y,n 为数字)= +/-n *10 y * (10 xy - 1) = 10 y *(一个仅由 9 组成的数字)= 一个能被 9 整除的数字。
举个例子。设原数为 1965,将其打乱后得到 6951。6951 - 1965 = 6*(1000-10) + 9*(100-100) + 5*(10-1) + 1*(1-1000) = 6*990 + 9*0 + 5*9 + 6*-999。注意,由于每个部分都能被 9 整除,因此减法后得到的数字也一定能被 9 整除,最终各位数字之和也能被 9 整除。
然后,这个技巧会要求你圈出一个除 0 以外的数字,并输入所有其他数字的和。程序只需在你输入的数字上加上一个数字,使和能被 9 整除即可。例如,如果你输入的数字和是 13,那么你圈出的一定是 5,因为 13 + 5 = 一个能被 9 整除的数字。
不能圈出零的原因是,如果您这样做了,然后输入一个已经被 9 整除的数字,那么程序将不知道您圈出的是 0 还是 9。
很棒的网站。我经常把它比作一个对概率和统计感兴趣的赌徒,但这个问题实际上与我的工作有关。我的人力资源部门坚持要求我按照钟形曲线对我的小团队(5人)进行评分——一个在所有员工中排名前5%,一个在其后的20%,一个在其后的50%,一个在其后的20%,还有一个在后5%。公司大约有5000名员工。这么小的样本量符合这个分布的概率有多大?
谢谢你的赞美。这道题很好。恰好有一名员工处于最低5%的概率是5*(.05)*(.95) 4 = 0.203627。假设有一名员工处于最低5%,那么恰好有一名员工进入接下来20%的概率是4*(.2/.95)*(.75/.95) 3 = 0.414361。假设有两名员工处于最低5%的概率,那么在剩下的75%中,恰好有一名员工进入接下来50%的概率是3*(.5/.75)*(.25/.75) 2 = 0.222222。剩下的两名员工中,有一人进入25%中最低20%的概率是2*(.2/.25)*(.05/.25) = 0.32。将所有这些概率相乘,我们得到 0.006,即 1% 的 3/5。
对于提出关于顺序统计量(第100列)问题的那位朋友,我有两个小问题:一个大问题,一个小问题。你的方法没有进行有限总体修正,我承认,对于5000名员工来说,这很容易做到,但如果只有20名员工,那肯定不行!
然而,更重要的是,你隐含地假设管理者对员工没有影响。假设优秀的管理者通过明智的招聘和解雇,或通过高于平均水平的激励技巧,提高了员工的平均水平。如果不考虑这种影响,我们最终的概率要么向上偏向,要么向下偏向。我相信你也知道这一点,但我对此很敏感,因为我在歧视案件中做过很多类似的计算,而未能调整那些我们可以调整的因素(在本例中是特定群体的影响)常常会让人误入歧途。
谢谢你提出的这些好观点。然而,如果无法控制工作绩效评分的分配,那么另一种选择就是评分膨胀。经理将被迫给出过高的评分,以取悦员工。作为一名在政府部门工作了十年的公务员,我对此有一些经验。我在内华达大学拉斯维加斯分校任教时,没有班级平均GPA标准,但对学期末的评分曲线有一定的预期。至少在大学里,我认为这是一项合理的政策。或许在商业环境中,某种符合常识的媒介也是最佳选择。
博彩数学家们面临着哪些著名的未解难题?比如博彩界的费马大定理。如果有,请举个例子。
好问题。我想不出什么。
这是如何工作的: www.1800gotjunk.com/genie/ ?
假设你的数字是 10t+u。要求你减去每个数字,得到 10t+utu = 9t,这个数字能被 9 整除。注意,所有能被 9 整除的数字都包含相同的项,也就是精灵预测的那个。
我即将参加专业执照考试。规定如下:
- 考试共设7个科目。
- 每门科目将有 60 道选择题。
- 每道多项选择题应有四个可能的答案,但只有一个正确答案。
- 为了通过考试,考生必须获得至少 75% 的总平均成绩,并且任何科目的成绩不得低于 65%。
我的问题是,如果考生所有答案都靠猜,他通过考试的概率有多大?换句话说,纯粹靠运气通过考试的概率有多大?
要满足75%的正确率,考生必须在420道题中至少答对315道。猜测的正确答案预期数量为420*0.25=105道。标准差为(420*0.25*0.75)^0.5 = 8.87412。因此,考生必须超出预期210道题,即210/8.87412=23.66432个标准差。做到这一点的概率高得离谱。如果地球上的每个人都参加这项测试,随机作答,我怀疑没有人或任何东西能通过。我甚至不想讨论另一个要求。
如果⼀所⼤学的⾜球队赢得⽐赛1的机会是10%、赢得⽐赛2的机会是 30%、两场⽐赛皆输的机会是65%, 他们刚好赢到⼀场⽐赛的机会是多 少?
如果我们假设⽐赛都是各⾃独⽴的, 那么输掉两场⽐赛的机率将是 90%*70%=63%. 不过既然你说输掉两场⽐赛的机率实际上为65%(这⽐起 63%还要⾼), 也就是说两场⽐赛是相关的。如果输掉两场⽐赛的机率是 65%、只输掉⽐赛2的机率是70%, 那么赢得⽐赛1并且输掉⽐赛2的机率 必须是5%. 运⽤相同的逻辑、输掉⽐赛1并且赢得⽐赛2的机率必须是 25%. 这样赢得两场⽐赛的机率只剩下5%. 所以刚好赢得⼀场⽐赛的机率 为 25%+5% = 30%.
在游戏节⺫「Let’s Make a Deal 让我们来做个交易」中, 那⾥有三扇⻔,举例来说, 其中两扇⻔后⾯各有⼀只⼭⽺, 另⼀扇⻔后⾯有⼀部新⻋。节⺫主持⼈Monty Hall会选出两位参赛者来选定⼀扇⻔。每次Monty都会打开⼀扇后⾯有⼭⽺的⻔, 让我们举例这是第⼀位参赛者。虽然Monty从未真的这样做过, 假使Monty在这时给其他参赛者机会去转换⻔的选择、改⽽去打开其他关闭的⻔, 他应该转换选择吗?
是的!这个问题的关键在于, 主持⼈总是会先打开有⼭⽺的⻔。他预先知道哪⼀扇⻔内有汽⻋, 所以⽆论参赛者选哪⼀扇⻔, 他总是能够先打开有⼭⽺的⻔。这个问题被称之为「Monty Hall悖论」, 它常会引起许多困惑、是因为这问题是被设计过的, 它错误地不说清楚主持⼈知道汽⻋藏在哪⾥,并总是在第⼀次就打开有⼭⽺的⻔。我想责备⼀下Marilyn Vos Savant, 她在她的专栏⾥糟糕地设计这个问题。让我们假设奖品就在1号⻔之后。以下是如果参赛者(第⼆位)有个策略不去转换选择的话。
- 参赛者选择1号⻔ --> 参赛者赢
- 参赛者选择2号⻔ --> 参赛者输
- 参赛者选择3号⻔ --> 参赛者输
以下是如果参赛者有个策略去转换选择的话、看看会发⽣什么事。
- 参赛者选择1号⻔ --> 主持⼈打开后⾯有⼭⽺的2或3号⻔ --> 参赛者转换选择其他的⻔ --> 参赛者输
- 参赛者选择2号⻔ --> 主持⼈打开后⾯有⼭⽺的3号⻔ --> 参赛者转换选择1号⻔ --> 参赛者赢
- 参赛者选择3号⻔ --> 主持⼈打开后⾯有⼭⽺的2号⻔ --> 参赛者转换选择1号⻔ --> 参赛者赢
所以参赛者若是不转换选择的话, 他有1/3赢的机会。参赛者若是转换选择的话, 他则有2/3赢的机会。因此参赛者肯定应该要转换选择。
阅读更多关于「Monty Hall悖论」, 我推荐这篇在 维基百科的⽂章。
我不同意你在2004年11月19日专栏中对蒙提霍尔问题的回答。假设汽车在1号门后面,奖品在1号门后面,那么实际上有以下四种可能性。
- 玩家选择门 1 --> 显示 2 --> 切换到 3,输
- 玩家选择门 1 --> 显示 3 --> 切换到 2,输
- 玩家选择门 2 --> 显示 3 --> 切换到 1,获胜
- 玩家选择门 3 --> 显示 2 --> 切换到 1,获胜
正如你所见,无论你换不换,获胜的概率都是50%。而且,认为换个更好,这完全违背常识。
你的错误在于假设每个事件都有25%的可能性。以下是每个事件的正确概率。
- 玩家选择门 1 (1/3) * 显示门 2 (1/2) = 玩家输 (1/6)
- 玩家选择门 1 (1/3) * 显示 3 (1/2) = 玩家输 (1/6)
- 玩家选择门 2 (1/3) * 显示 3 (1/1) = 玩家获胜 (1/3)
- 玩家选择门 3 (1/3) * 显示 2 (1/1) = 玩家获胜 (1/3)
因此失败事件的总概率为 2*(1/6) = 1/3,获胜事件的总概率为 2*(1/3)=2/3。
有五种不同的配料可供选择,您可以制作多少种不同的披萨,以及多少种配料?
有 1 种做法,0 种配料;5 种做法,1 种配料;10 种做法,2 种配料;10 种做法,3 种配料;5 种做法,4 种配料;还有 1 种做法,5 种配料。所以答案是 1+5+10+10+5+1 = 32。另一种解法是,可以加配料,也可以不加。所以总数是 2 +5 = 32。
我上周在报纸上看到,印度尼西亚最近一次遭受破坏的地震发生在12月26日。报纸还显示,在过去100年里发生的八次最致命的地震中,有三次发生在12月26日。我想知道,考虑到以下事实,同一天发生三次大地震的概率有多大:这种震级(8.0级或更大)的地震每年只发生一次。上一次大地震恰好发生在一年前,2003年12月26日,发生在伊朗(连续发生的概率?)。期待您的回复。
在发现佛罗里达飓风只袭击布什选区县的说法纯属骗局(参见2004年10月17日专栏)后,我对这种所谓的巧合更加怀疑了。根据美国国家地震信息中心的数据,自1990年以来发生的11次最大地震中,只有最近的一次发生在2004年12月26日。你提到的伊朗地震只有6.7级,远未进入前八名。
如果你每天卖出一半鸡蛋,再加上半个鸡蛋,那么一开始你有多少个鸡蛋?三天后,鸡蛋数量为零。每天结束时,鸡蛋数量都是整数。
设d(代表白天)表示一天开始时鸡蛋的数量,n(代表夜晚)表示一天结束时鸡蛋的数量。问题告诉我们d/2 - ? = n。那么,我们用n来解d。
d/2 = n + ?
d=2n+1
所以第三天 n=0,所以 d=1。
第二天n=1,所以d=3。
第三天n=3,所以d=7。
所以,你一开始就有 7 个鸡蛋。
想象一下,一个岛上居住着10个人,岛上的政策是这样的:每天随机选出一名岛民担任酋长,任期恰好一天;一天过去后,再随机选出另一名岛民(因此,刚刚担任酋长的岛民再次担任酋长的概率为1/10)。需要解决的问题是:平均而言,每个岛民至少担任一次酋长需要多少天?
只需1天就能选出1个人担任酋长。第二天出现新酋长的概率为0.9。如果每天的概率为0.9,那么产生新酋长的预期天数为1/0.9 = 1.11。这对于任何概率都成立:成功的预期尝试次数为1/p。因此,在2人担任酋长后,第二天出现新酋长的概率为0.8。因此,等待第三位酋长的时间为1/0.8 = 1.25天。答案是等待时间的总和,即1/1 + 1/.9 + 1/.8 + ... + 1/.1 = 29.28968天。
圆的半径为1。三角形是等边三角形。求每个颜色区域的面积。
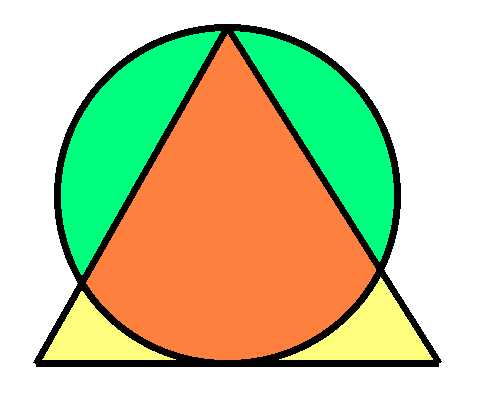
我不想把答案透露给那些想自己解决的人。想要获取答案和解答,请访问我的另一个网站mathproblems.info ,问题 189。
假设你赢得了一场比赛,在一场NBA比赛中场休息时,你有机会罚球,如果罚中,你将赢得100万美元。此外,你可以继续罚球,双罚或不罚,直到罚球不中或选择停止。如果你的罚球命中率是75%,你会在什么时候停下来?你会停下来吗?到了某个时候,金钱对你来说变得越来越不重要了。你会怎么做?
在某些时候,你应该拒绝一个好的赌注,因为赌注太高了。我个人认为衡量一个人从金钱中获得的快乐程度的一个好方法是对金额取对数。对数的底数并不重要,所以我们使用 10。但是我们不能取小于 10 的对数,所以我们假设对于小于 10 的任何金额,快乐程度都是 0。所以在你的例子中,我们假设你在第一次罚球赢得 1,000,000 美元之前拥有 0 美元。现在你有 log(1,000,000) = 6 个单位的快乐。你再次罚球的快乐预期值是 0.75*log(2,000,000) + 0.25*0 = 4.975772。这小于 6,所以在这种情况下你应该拿走一百万美元然后走开。但是如果你已经有一些钱,情况可能会有所不同。假设你已经有 200,000 美元。那么,你放弃下注的幸福感是 log(1,200,000) = 6.07918。你冒着百万风险再赌一把的幸福感是 0.75*log(2,200,000) + 0.25*log(200,000) = 6.082075,所以你勉强选择第二次。如果你赢了那一次,你的选择将是 log(2,200,000) = 6.34242 和 0.75*log(4,200,000) + 0.25*log(200,000) = 6.29269 之间。在这种情况下,你不应该再赌第三次,而是选择放弃这 2,000,000 美元的奖金。接受第一次双倍下注的盈亏平衡点是现有财富 191,487 美元。要接受两次双倍下注,你需要有 382,975 美元的其他资金。
我记得如果一个房间里有22个人,那么有两个人过同一天生日(月份和日期,而不是年份)的概率是相等的。我忘了怎么算才能证明这一点了。请问您能提供一下吗?
我想我之前回答过这个问题,但 50/50 的概率更接近 23。为了简单起见,我们忽略闰年。详细答案是,以某种方式对这 23 个人进行排序。2 号人生日与 1 号人生日不同的概率是 364/365。假设 1 号人和 2 号人生日不同,那么 3 号人生日与 1 号人和 2 号人生日不同的概率是 363/365。如此反复,直到 23 号人。因此,概率为 (364/365)*(363/365)*...*(343/365) = 49.2703%。因此,不匹配的概率为 49.27%,至少匹配一个的概率为 50.73%。 Another solution is the number of permutations of 23 different birthdays divided by the total number of ways to pick 23 random numbers from 1 to 365, which is permut (365,23)/365 23 = 42,200,819,302,092,400,000,000,000,000,000,000,000,000,000,000,000,000,000,000 / 85,651,679,353,150,300,000,000,000,000,000,000,000,000,000,000,000,000,000,000 = 49.27%.
某州教师的周薪呈正态分布,均值为490美元,标准差为45美元。随机抽取一位教师,周薪超过525美元的概率是多少?我不记得如何只根据均值和标准差,而不考虑总体数据来计算概率。
这意味着价格高于平均水平35美元,或7/9个标准差。高于预期7/9个标准差以上的概率为1-Z(7/9) = 1- 0.78165 = 0.21835。
两个人正在玩石头剪刀布。假设这个游戏不涉及策略。如果玩的是“三局两胜制”,玩家A赢得第一轮,那么玩家B获胜的概率是多少?
玩家 B 需要赢得接下来的两场比赛(不包括平局),因此概率为 (1/2)*(1/2) = 1/4。
你好,我想问你这个问题,因为我在网上找不到。希望你能回答我的问题:存在的可能性有多大?无论是在地球上还是在宇宙的其他地方?这不是一个赌博问题,而是一个我们都应该知道的答案,这样我们才能体会到,活着究竟能战胜多少困难!
我认为银河系中任何地方存在智慧生命的可能性都非常高。德雷克方程式试图估算银河系中智慧生命的数量,根据输入的数字,得出的数字大约是一百万。然而,也没有确凿的证据表明这些文明曾经访问过我们或与我们进行过接触。所以著名的费米问题是“他们都在哪里?”我确实认为缺乏其他智慧生命存在的证据对德雷克方程式产生了一些怀疑,但我仍然认为我们银河系中智慧文明的数量大约在1000个左右。这还只是我们银河系,外面还有数十亿个星系。然而,星系之间的距离如此之大,讨论它们之间的旅行或交流真的没有多大意义。所以回答你的问题,我认为大约是99.9%。
假设一家酒店有 10,000,000 个房间,电子钥匙数量为 10,000,000 把。由于计算机出错,每把钥匙都被编入一个随机密码,正确率只有 1/10,000,000。酒店房间已满。至少有一位顾客持有可用钥匙的概率是多少?
精确答案:1-(9,999,999/10,000,000) 10,000,000 = 0.632121。这与 (e-1)/e 精确到小数点后七位相同。
考试中有75道选择题。每道题有4个可能的答案,只有1个正确。考试的及格分数是50%。猜对每个答案通过考试的概率是多少?
635,241 中 1 个。
对于赛中投注,如果一名网球运动员赢得一场比赛的概率为“p”,那么他赢得一盘比赛的概率是多少?
据我理解,网球规则规定,一盘比赛的胜者是率先赢得六局,且净胜至少两局的一方。6-6平局将进行一局决胜。下表显示了在已知胜局概率的情况下,赢得一盘比赛的概率。
网球中的概率
| 可能性 游戏胜利 | 可能性 盘胜 |
| 0.05 | 0.000003 |
| 0.1 | 0.000189 |
| 0.15 | 0.001899 |
| 0.2 | 0.009117 |
| 0.25 | 0.028853 |
| 0.3 | 0.06958 |
| 0.35 | 0.138203 |
| 0.4 | 0.23687 |
| 0.45 | 0.361085 |
| 0.5 | 0.5 |
| 0.55 | 0.638915 |
| 0.6 | 0.76313 |
| 0.65 | 0.861797 |
| 0.7 | 0.93042 |
| 0.75 | 0.971147 |
| 0.8 | 0.990883 |
| 0.85 | 0.998101 |
| 0.9 | 0.999811 |
| 0.95 | 0.999997 |
赢得游戏 p 和输掉 q 的概率公式为 1*p 6 + 6*p 6 *q + 21*p 6 *q 2 + 56*p 6 *q 3 + 126*p 6 *q 4 + 252*p 7 *q 5 + 504*p 7 *q 6
你在一个淡水湖上,乘着船,船上有一块石头。你把石头扔进湖里。相对于陆地(岸边),湖水位是上升、下降还是保持不变?我的同事认为水位会保持不变。
相对于岸边的水位将会下降。在船内,岩石向下压着独木舟,从而将周围的水向上推。排开的水量等于岩石的重量。例如,一块10磅重的岩石将向上排开10磅的水。当岩石被抛到海里时,重量不再重要,重要的是岩石的体积。因此,岩石将向上推开与其体积相等的水。岩石的质量大于水的质量,因此岩石向下排开的水比岩石本身排开的水更多。因此,当岩石在独木舟中时,湖面水位将高于湖底。
这是如何运作的?
- 拿一个计算器。(你无法在脑子里做这件事)
- 输入您的电话号码的前三位数字(不是区号)
- 乘以 80
- 加 1
- 乘以 250
- 添加您的电话号码的后 4 位数字
- 再次添加您的电话号码的最后 4 位数字。
- 减去 250
- 将数字除以 2
你认得答案吗?
假设你的电话号码的前三位数字为 x,后四位数字为 y。现在看看每一步的结果。
- 准备好!
- 十
- 80倍
- 80x+1
- 250*(80x+1) = 20000x+250
- 20000x+250+y
- 20000x+250+2y
- 20000x+250+2y-250 = 20000x+2y
- (20000x+2y)/2 = 10000x+y
所以这当然等于你的电话号码。我们需要 10000x 将前缀向左移动四位,然后加上最后四位数字。
有一场价值 27,000 美元的汽车抽奖,彩票售价为六张 500 美元,或一张 100 美元。目前已售出 68 张彩票,明天是购买截止日期。我知道,要达到 50% 的中奖概率,我必须花费 5666.44 美元;要达到 66.66% 的中奖概率,我必须花费 11,332.88 美元(对吗?)。我应该花多少钱(或者说我必须买多少张彩票)才能确保我“赢得”这辆车?(90%?95%?)这个抽奖活动值得参加吗?还是我必须花掉买车的钱?
关于1/2和2/3的概率,你的说法是对的。如果你买了t张彩票,你的中奖概率是t/(68+t)。所以,对于90%的概率,t的解法如下。
0.9 = t/(68+t)
0.9*(68+t) = t
61.2 = 0.1吨
t = 612,即 51,000 美元
对于 95% 来说...
0.95=t/(68+t)
0.95(68+t) = t
64.6 = 0.05吨
t = 1292,或 107,666.67 美元
假设这辆车对你来说价值 27,000 美元,那么一旦售出的下一张彩票不能增加你中奖的概率以保证其价值,你就应该停止购买彩票。
为了使彩票物有所值,它应该将您中奖的概率提高 p,其中...
27000*p=(500/6)
p=0.003086
假设您购买了 t 张票,但您并不想再买一张票。
[(t+1)/(t+68+1)] − [t/(t+68)] = 0.003086
[(t+1)/(t+69)] − [t/(t+68)] = 0.003086
[((t+1)*(t+68))/((t+69)*(t+68))] − [(t*(t+69))/((t+68)*(t+69))] = 0.003086
[(( t2 +69t+68)/((t+69)*(t+68))] − [( t2 +69t)/((t+68)*(t+69))] = 0.003086
68/((t+68)*(t+69)) = 0.003086
((t+68)*(t+69)) = 220.32
t2 +137t+4692=22032
t2 +137t-17340=0
t=(-137+/-(137 2 -4*1*-17340) 2 )/2
t = 79.9326
让我们通过插入一些购买门票的价值来测试这一点,假设玩家总是可以以每张 500 美元/6 = 83.33 美元的价格购买门票。
如果有 79 张彩票,您的成本为 79*(500/6) = 6,583.33 美元,您中奖的概率为 79/(79+68) = 53.74%,您的预期回报为 27,000 美元*0.5374 = 14,510.20 美元,您的预期利润为 14,510.20 美元 - 6,583.33 美元 = 7,926.87 美元。
80 张彩票的成本为 80*(500/6) = 6,666.67 美元,中奖概率为 80/(80+68) = 54.04%,预期回报为 27,000 美元*0.5405 = 14,594.59 美元,预期利润为 14,594.59 美元 - 6,666.67 美元 = 7,927.92 美元
81 张彩票的成本为 81*(500/6) = 6,750.00 美元,中奖概率为 81/(81+68) = 54.36%,预期回报为 27,000 美元*0.5436 = 14,677.85 美元,预期利润为 14,594.59 美元 - 6,750.00 美元 = 7,927.85 美元。
因此我们可以看到,最大预期赢利额在 80 张票时达到峰值。
我正在尝试比较现在更换旧冰箱以节省电费与等到它坏了再更换的成本。我可以计算出新冰箱比旧冰箱便宜多少:每年 37 美元,这很容易。但是我该如何计算新冰箱的成本呢?假设新冰箱的价格为 425 美元。我不能说这 425 美元*全部*都是新的支出,因为我*总有一天*要更换旧冰箱,如果不是现在的话,所以无论如何我迟早都会有这笔新冰箱的费用。假设一台普通冰箱的使用寿命为 14 年,而我的旧冰箱已经用了 9 年,所以如果我现在更换它,那么 5 年后就需要更换它了。我尝试制作一个两列表格,比较使用现有冰箱9年后更换的成本和现在更换的成本,但我不知道如何进行同类比较,因为我不知道要考虑未来多久的成本,而且冰箱的更换年份也不同。我该如何比较现在更换和以后更换的经济性呢?顺便说一句,这不是针对我自己的情况,因为我现在的冰箱大概已经用了30年了。这是给一个朋友买的。
如果您继续使用现有的冰箱,那么五年后,与购买新冰箱相比,您将多花 37 美元*5 = 185 美元的电费。如果您现在更换冰箱,您将损失 425 美元,但假设五年后仍按线性折旧计算,其价值仍为 425 美元*(9/14) = 273.21 美元。因此,您将因折旧而损失 425 美元*(5/14) = 151.79 美元。因此,新冰箱的折旧成本低于保留旧冰箱的额外电费,所以我建议现在就购买新冰箱。
如果有三个人,那么至少有两个人的生日是同一天的概率是多少。
忽略闰日,三个生日不同的概率为 (364/365)*(363/365) = 0.99179583。因此,至少有一个生日相同的概率为 1 - 0.99179583 = 0.00820417。
一个房间里有五个人。其中至少有两个人出生在同一月份的概率是多少?
为了简单起见,我们假设每个人出生在不同月份的概率为 1/12。五个人出生在不同月份的概率为 (11/12)*(10/12)*(9/12)*(8/12) = 0.381944。因此,五个人出生在同一月份的概率为 1 - 0.381944 = 0.618056。
我们在工作中遇到了一个难题——纯粹为了好玩,结果谁也想不出来。一位农民有五辆拖车,装满了羊。其中四辆拖车的羊重39公斤,第五辆拖车的羊重40公斤。所有的羊都长得一模一样。他去市场,想找出哪辆拖车里的羊重40公斤,而他只能用一次大秤!!!他是怎么做到的?请帮帮忙,我工作的地方快把我们都逼疯了——这可是兽医诊所啊!!
答案就在专栏的末尾。
回答羊的问题
从拖车 1 中取出一只羊,从拖车 2 中取出两只,从拖车 3 中取出三只,从拖车 4 中取出四只,从拖车 5 中取出零只。如果所有羊的重量为 39 公斤,那么总重量为 39 * 10 = 390 公斤。然而,0 到 4 只羊的重量会比 1 公斤重。如果总重量为 391,那么秤上有一只较重的羊;因此它一定来自拖车 1。同样,如果总重量为 392,那么秤上有两只较重的羊,它们一定来自拖车 2。同样,重量为 393 表示较重的羊在拖车 3 中,重量为 394 表示较重的羊在拖车 4 中,重量为 390 表示较重的羊在拖车 5 中。
在一架有 180 个座位的飞机上,我坐在与我所看到的同一航班的漂亮女孩旁边的概率有多大?
这取决于座位集群的数量。大多数国内航班过道两侧各有三个座位。这样一来,就有60个三座集群。你们中第一个人就座后,剩下的179个座位中,会有两个座位位于同一集群,所以位于同一集群的概率是2/179 = 1.12%。那么,中间座位就不可能有其他人了。第三个人坐在中间座位的概率是1/3。所以答案是(2/179)*(2/3) = 0.74%,也就是1/134.25。
三位逻辑学家正在玩一个游戏。每个人都必须秘密写下一个正整数。写下最小唯一整数的逻辑学家将赢得3美元。如果三位逻辑学家都写下相同的数字,则每人将赢得1美元。这三位逻辑学家都很自私,都想最大化自己的奖金。游戏不允许交流。那么,每位逻辑学家会采取什么策略呢?
答案将出现在下一栏中。
我读到一篇报道,沃伦·巴菲特(世界第三大富豪)抱怨说,他只缴纳17.7%的联邦税,而他的秘书却缴纳了30%。我觉得这太离谱了。你能评论一下吗?
通常我会说这超出我的专业范围。然而,作为一名在政府部门工作了八年的精算师,我对税收略知一二。据我所知,沃伦·巴菲特的大部分收入被定义为资本利得,税率仅为15%。不管你喜不喜欢,税法允许这样做。让我感到困惑的是,为什么他的秘书要缴纳高达30%的税。根据这段视频,他计算的是“工资税和所得税”。他所说的“工资税”显然是指社会保障税和医疗保险税。让我们看看30%对他的秘书来说是否是一个合理的联邦总税率。
2007 年最高税率为 35%,但这只适用于 349,700 美元以上的收入。该点之前的收入征税要少得多。假设他的秘书是单身,没有受抚养子女,她的工资为 100,000 美元。首先,我们减去最低扣除额。2007 年单身申报者的标准扣除额为 5,350 美元。个人扣除额为 3,400 美元。因此,我们还剩下 100,000 美元 - 5,350 美元 - 3,400 美元 = 91,250 美元的应纳税收入。对于 2007 年的单身申报者,收入的前 7,825 美元税率为 10%,然后是 15% 至 31,850 美元,然后是 25% 至 77,100 美元,因此,她的所得税应为:0.1×7,825美元+0.15×(31,850美元-7,825美元)+0.25×(77,100美元-31,850美元)+0.28×(91,250美元-77,100美元) = 19,660.75美元。这仅占她收入的19.7%。我所有的假设,例如她的收入、报税身份以及不逐项申报,都对她不利,或者说,她的税率更高。
现在我们来算算社会保障和医疗保险。2007年,社会保障税为6.2%,最高可达97,500美元,之后就完全取消了。2007年的医疗保险税率为1.45%,没有上限。所以,她的社会保障税和医疗保险税合计为6.2%*97,500美元+1.45%*100,000美元=7,495美元。算上这些税款,她的总税率为(19,660.75美元+7,495美元)/100,000美元=27.2%。但距离30%的目标仍然差2.8%。
我猜测她可能也考虑到了最终是她要为雇主支付相应的社会保障和医疗保险税。对于那些不知道的人来说,社会保障和医疗保险税实际上是从你的支票中扣除的两倍。雇主支付另一半。然而,包括我在内的一些人认为最终是雇员要支付这两项费用。如果雇主不必缴纳那项税,他就有更多的钱支付员工工资。当你像我一样是自雇人士,必须支付这两部分费用时,很容易有这种感觉。如果你将社会保障/医疗保险税翻倍,税率现在是(19,660.75 美元 + 2×7,495 美元)/100,000 美元 = 34.7%。我猜这 4.7% 的差额是因为她赚得不到 100,000 美元、已婚、有受抚养人、逐项列出扣除额或以上几种情况的综合作用。
社会保障税和医疗保险税对沃伦·巴菲特来说影响不大。首先,97,500 美元的社会保障上限对他来说微不足道。其次,这些税适用于工资,而不是资本利得,因为他将自己的大部分收入定义为资本利得。
所以,这是我对巴菲特先生言论背后的数学原理的最佳猜测。
更新:这篇专栏文章发表后不久,我收到了以下回复。为了公平起见,我提出以下论点:巴菲特先生缴纳的税款过多。
我饶有兴趣地读了你对那位“愤怒”人士的回答,他觉得沃伦·巴菲特缴纳的税款比例比他的秘书还低,这太不公平了。我对你的回答感到失望,因为它没有纠正暗示巴菲特缴纳的税款比他的秘书还少的错误信息。首先,正如您所说,投资收入确实要按15%的税率征税。这实际上是双重征税,因为巴菲特先生投资的劳动收入是按他36%的边际税率征税的。这就像苹果和橘子(工作收入和投资收入)的比较。
其次,不应该只看百分比。用赌博的术语来说,应该看“赔付”。我非常肯定,巴菲特先生当年缴纳了数百万美元的税款,而他的秘书只缴纳了数千美元。你的读者难道不应该更加愤怒吗?一个国家公民为同样的政府服务缴纳的税款比其他公民高出数千倍?人们完全可以毫不犹豫地说:“我听说沃伦·巴菲特缴纳的税款比他的秘书多一百万倍,这太离谱了!”
我只是想指出,只看“百分比”而不看“实际赔付”是谬论。这和你很多赌博谬论类似。
此致,
凯文·A.(达拉斯)
感谢您收集的这些有趣的数学谜题。我和我的女朋友想出了这个海盗谜题的变种。如果所有海盗的等级相同,并且每轮都通过抽签决定分配方案的提议者,会怎么样?在这个变种中,假设每个海盗的首要任务是最大化他预期获得的金币数量。我找到了我认为的答案,但也许你想先尝试一下。再次感谢。
不用客气。如果只剩下两个海盗,那么被选中提出建议的那个海盗就没希望了,因为另一个海盗会投反对票。被抽中的那个海盗会得到零分,另一个海盗则会得到全部1000分。所以,在抽签之前,剩下两个海盗的预期价值是500个硬币。
在三海盗阶段,抽到的海盗应该建议给其他海盗中的一位501,给自己499。抽到501的海盗会投赞成票,因为它比投反对票的预期值500要高。抽奖前,剩下三位海盗,你分别有1/3的概率得到0、499或501枚硬币,平均333.33枚。
在四海盗阶段,抽到的海盗应该选择将 334 枚硬币给其他任意两名海盗,并给自己 332 枚。这样一来,他就能从获得 334 枚硬币的海盗那里获得两票“赞成”,因为他们宁愿要 334 枚硬币,也不愿要 333.33 枚。算上你自己的一票,你将获得 4 票中的 3 票。抽签前,每位海盗的期望值是 0、334、334 和 332 的平均值,即 1000/4=250。
按照同样的逻辑,在五个海盗的阶段,抽到的海盗应该选择给任意两个海盗251,给自己498。与原题不同,这里不需要倒推。只需用硬币数量除以海盗数量(不包括你自己)。然后把一半的海盗(向下取整)的平均值加上一枚硬币。
我需要帮助解决一个名为“永恒二号”的谜题。解开谜题的奖金高达200万美元,对我来说是一笔巨款。这里有一个采访链接,采访内容包括游戏开发者克里斯托弗·蒙克顿(他曾担任玛格丽特·撒切尔的顾问)。这款游戏显然与赌博无关,但尽管如此,或许你可以在你的网页上添加一两句相关内容。
游戏开发者在上面给出的链接里吹嘘这个谜题无法解决。我开始觉得他其实是对的,而且他自己是唯一一个最终会通过出售这个(荒谬却引人入胜的)游戏致富的人。作为一名数学家,你会如何解决这种类型的谜题呢?
希望你开心!过去一个月左右,我一直对这个拼图着迷。我很幸运(或许是不幸)在当地的Borders书店找到了这个256块的拼图,但我不得不在eBay上从一个澳大利亚人那里买下那四个线索的拼图。
我编写了一个程序,可以轻松解决这四个线索谜题。它不到一秒钟就解开了包含 72 个方块的线索谜题 #4。我采用的是一个简单的暴力递归程序。我在棋盘上规划了一条路径,从边界开始。在每个位置,程序都会循环遍历所有未使用的方块,寻找一个合适的方块。如果找到,就移动到下一个格子;如果没有找到,就后退一个格子。
我用两台电脑连续数周解开这道256块、价值200万美元的谜题,却都远不及格。我倾向于同意创作者在视频中所说的话:即使你把一千万台世界上最快的电脑连接起来,它们也未必能在宇宙毁灭前找到答案。你可能会认为我会在开始之前听从他的警告,但面对一个优秀的谜题,我所有关于时间利用的考虑都抛到九霄云外了。
我有很多捷径的想法,但即使它们能把我的程序速度提高十亿倍,可能也无济于事。如果有人能解决这个问题,我会非常钦佩。真正让我感到不安的是,我感觉数学中存在一些未被发现的分支,可以轻松解决这样的难题。在那之前,我认为我们能做的最好的就是美其名曰的反复试验。今天的计算机实在太慢了,组合数量又太多,这种方法的成功率不高。

假设两座城市之间的距离是1000英里。在无风条件下,飞机可以以500英里/小时的速度飞行。那么,在无风条件下,往返飞行需要更长的时间吗?或者,在一个方向上有100英里/小时的顺风,在另一个方向上有相同的逆风?
在无风的情况下,单程飞行需要2小时,总共需要4小时。顺风时,飞机的速度为600英里/小时,飞行时间为1000/600=1.667小时。逆风时,飞机的速度为400英里/小时,飞行时间为1000/400=2.5小时。因此,在顺风的情况下,总飞行时间为4.167小时,比顺风时长多了10分钟。
这恰恰表明,对平均值进行平均是危险的。你不能说,如果一个行程的平均速度是 500 英里/小时,而另一个行程是 600 英里/小时,那么整个行程的平均速度就是 500 英里/小时,因为 400 英里/小时的路程涵盖了更长的时间。
如果这不直观,想象一下500英里/小时的风速。飞机顺风飞行需要1个小时,但逆风飞行则需要很长时间。
我最近参加了一个抽奖活动,奖品有7033个,据说中奖概率是1/13。我买了5张彩票。我实际中奖概率是多少?另外,大奖有40个。我中大奖的概率是多少?
为了简单起见,我们忽略这样一个事实:你买的彩票越多,每张彩票的价值就越低,因为你是在与自己竞争。也就是说,输掉五张彩票的概率是 (12/13) 5 = 67.02%。所以至少赢得一次奖的概率是 32.98%。在你买彩票之前,彩票桶里总共有 7033×13=91,429 张彩票。91,429-40=91,389 张彩票不是大奖。五张彩票中不了大奖的概率是 (91,389/91429) 5 = 99.78%。所以至少赢得一次大奖的概率是 0.22%,也就是 458 分之一。
我有一个难题,已经尝试解了几个月,但毫无进展。如果时间允许,希望您能帮我解答一下,因为它让我彻夜难眠 :-)。总之,在《超越计数——附录 CAA》的词汇表中,有三个由数字和字母组成的序列作为“魔法数字”的词条。其中一个数字甚至出现在了书的封面上,所以我猜它们一定很重要。您有什么看法吗?
我很少这么说,但我确实不知道。正如你在另一封邮件中提到的,他们采用的是美国货币序列号的格式,两个字母中间加一个十位数字。出于对版权的尊重,我不会在这里指出这些数字的具体含义。
我很好奇《永恒2》的谜题挑战结果怎么样了。它解决了吗?你还在继续努力吗?
谢谢你的提问。不,自从我在2008年11月17日的“问问巫师”专栏里写了这篇文章之后,我就没再碰过这个问题。根据他们的网站,他们会在2009年12月31日设定“审查日期”,如果有必要,还会在2010年设定。在我看来,这个问题永远也解决不了。
更新:Eternity II 网络尺寸似乎不再存在。
我饶有兴致地读着“巫师”博客上关于阿诺德·施瓦辛格否决信的报道。我的问题与州长那荒谬却又意料之中的回应有关。州长声称这只是一个“荒诞的巧合”。尽管有压倒性的间接证据(该法案的发起人和收信人正是一周前辱骂州长的人),你能否估算一下,一封恰好只有七行的信偶然拼出这句话的概率有多大?我认为,考虑到所使用的字母,这比仅仅给每个字母分配1/26的概率还要小得多。U、Y,尤其是K,似乎不是常用的单词开头字母。
如果您容易被冒犯,请跳到下一个问题。
为了让那些没有读过那篇博客的读者了解一下,请看一下加州州长阿诺德施瓦辛格的这份备忘录(PDF)中每一行的首字母,从以字母 F 开头的行开始。
我的同伴网站“Wizard of Vegas”讨论过这个问题。为了找到答案,我在维基百科上查找了英语中第一个单词每个字母的频率。
按首字母排列的词频
| 信 | 频率 |
| 一个 | 11.60% |
| B | 4.70% |
| C | 3.51% |
| D | 2.67% |
| 埃 | 2.00% |
| F | 3.78% |
| 格 | 1.95% |
| 哈 | 7.23% |
| 我 | 6.29% |
| J | 0.63% |
| 钾 | 0.69% |
| 左 | 2.71% |
| 米 | 4.37% |
| 否 | 2.37% |
| 哦 | 6.26% |
| 磷 | 2.55% |
| 问 | 0.17% |
| R | 1.65% |
| 秒 | 7.76% |
| T | 16.67% |
| ü | 1.49% |
| 五 | 0.62% |
| 西 | 6.66% |
| 十 | 0.01% |
| 是 | 1.62% |
| Z | 0.05% |
要估算阿诺德的信息确实只是巧合的概率,其公式为:Prob(F) × Prob(U) × ... × prob(U) = 0.0378 × 0.0149 × 0.0351 × 0.0069 × 0.0162 × 0.0626 × 0.0149 = 486,804,391,348 分之一。这甚至还没有考虑到两个单词之间的空格恰好被换行符替代。
我要感谢 Eliot J. 和 Jonathan F. 对此解决方案的贡献。
在机场的行李传送带上,我需要取的行李越多,等待所有行李出来所需的时间就越长。如果我只有一个行李,我可能需要等到大约一半的行李出来。如果我带了两个行李,我的等待时间会更长,如果带了三个,等待的时间就更长了。假设我的行李随机地混在一起,那么根据我的行李数量和行李总数,我需要等待多少行李出来才能取回所有行李,这个通用公式是什么?
我们先定义一些变量,如下:
n = 您的行李数量
b = 行李总数
随着行李总数的增加,答案将越来越接近 b×n/(n+1)。对于大型飞机来说,这个答案会比较准确。但是,如果你想要更精确的答案,答案是
[b× combin (b,n)-(combin(i,n) 中 i=n 到 b-1 的和)]/combin(b,n)
例如,如果总共有 10 个行李,其中 4 个是您的,那么预计等待时间 =
[10×combin(10,4)-combin(4,4)-combin(5,4)-combin(6,4)-combin(7,4)-combin(8,4)-combin(9,4)]/combin(10,4) = 8.8 袋。
解决方案:
从 b 个袋子中取出 n 个袋子的方法数为 combin(b,n)。因此,所有袋子都出现在前 x 个袋子中的概率为 combin(x,n)/combin(b,n)。最后一个袋子是第 x个袋子的概率为 (combin(x,n)-combin(x-1,n))/combin(b,n),其中 x>=n+1。x=n 时,概率为 1/combin(b,n)。
因此,预期等待时间与总等待时间的比率为:
n×组合(n,n)/组合(b,n) +
(n+1)×(组合(n+1,n)-组合(n,n))/组合(b,n) +
(n+2)×(组合(n+2,n)-组合(n+1,n))/组合(b,n) +
。
。
。
+
(b-1)×(组合(b-1,n)-组合(b-2,n))/组合(b,n) +
b×(combin(b,n)-combin(b-1,n))/combin(b,n)
取伸缩总和,可以简化为:
[b×combin(b,n)-combin(b-1,n)-combin(b-2,n)-...-combin(n,n)]/combin(b,n)
后来有一位读者来信说,答案可以简化为 n×(b+1)/(n+1)。这可以用归纳法来证明,虽然方法合法,但总让我感到不满足。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
我卖雕塑。平均每卖出七件雕塑,就有一件是乌龟,其余都是其他类型的雕塑。如果我想在接下来的100件雕塑销售中,有90%的几率不缺货,我需要库存多少件乌龟?

令 t 为制造的乌龟数量,x 为售出的数量。
pr(x<=t)=0.9
pr(x-14.29<=t-14.29)=0.9
pr((x-14.29)/3.5)<=(t-14.29)/3.5))=0.9
不等式左边服从标准正态分布(均值为0,标准差为1)。下一步需要学习统计学入门课程,或者具备一定的信念才能接受。
(t-14.29)/3.5 = normsinv(0.9) 这是 Excel 函数。
(t-14.29)/3.5 = 1.282
t-14.29 = 4.4870
t = 18.77
没人会买0.77个乌龟雕像,所以我会凑整到19个。根据二项分布,卖出18个或更少乌龟雕像的概率是88.35%,卖出19个或更少乌龟雕像的概率是92.74%。这个问题是在我的同伴网站“维加斯巫师”的论坛上提出并讨论的。
五名水手在海难中幸存下来。他们做的第一件事就是收集椰子,并把它们堆成一个大堆。他们原本打算事后平分,但辛苦采摘椰子之后,他们实在太累了。于是他们晚上睡觉,打算明天早上再分椰子。
然而,水手们彼此并不信任。午夜时分,其中一个人醒来,想要拿走属于自己的那一份。他把椰子堆分成五等份,只剩下一个。他把自己的那份埋了起来,把其他四堆椰子合并成一个新的公共椰子堆,然后把剩下的椰子给了一只猴子。
凌晨 1 点、2 点、3 点和 4 点,其他四名水手也做着同样的事情。
第二天早上,没人承认自己做了什么,他们按照原计划平分椰子。他们又剩下一个椰子,给了猴子。
原始堆中椰子的最小可能数量是多少?
“向下滚动 100 行即可找到答案。
1
2
3
4
5
6
7
8
9
10
11
12
十三
14
15
16
17
18
19
20
21
22
23
24
二十五
二十六
二十七
二十八
二十九
三十
31
三十二
33
三十四
三十五
三十六
三十七
三十八
三十九
40
41
四十二
43
四十四
45
46
四十七
四十八
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
原先那堆椰子一共有15621个。再向下滚动100行,查看我的答案。
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
设 c 为原始堆中椰子的数量,f 为最后一次分配后每个水手的最终份额。
水手 1 拿走他的那一份并将他的椰子给猴子后,将剩下 (4/5)×(c-1) = (4c-1)/5。
水手 2 拿走他的那一份并将他的椰子给猴子后,将剩下 (4/5)×(((4c-1)/5)-1) = (16c-36)/25。
水手 3 拿走他的那一份并将他的椰子给猴子后,将剩下 (4/5)×(((16c-36)/25)-1) = (64c-244)/125。
当水手 4 拿走他的那一份并将他的椰子给猴子后,将剩下 (4/5)×(((64c-244)/125)-1) = (256c-1476)/625。
当水手 5 拿走他的那一份并将他的椰子给猴子后,将剩下 (4/5)×(((256c-1476)/625)-1) = (1024c-8404)/3125 个。
第二天早上,每个水手所占的剩余份额为 f = (1/5)×(((1024c-8404)/3125)-1) = (1024c-11529)/15625。
那么,问题是,c 的最小值是多少,使得 f=(1024×c-11529)/15625 为整数。让我们用 f 来表示 c。
(1024×c-11529)/15625 = f
1024c - 11529 = 15625×f
1024c = 15625f+11529
c = (15625f+11529)/1024
c = 11 + ((15625×f+265)/1024)
c = 11+15×f+(265×(f+1))/1024
那么,使得 265×(f+1)/1024 为整数的最小 f 是多少?265 和 1024 没有共同的因数,所以 f+1 本身必须能被 1024 整除。f+1 的最小可能值为 1024,因此 f=1023。
因此,c = (15625×1023+11529)/1024 = 15,621。
以下是每个人和猴子收到的椰子数量:
椰子问题
| 水手 | 椰子 |
| 1 | 4147 |
| 2 | 3522 |
| 3 | 3022 |
| 4 | 2622 |
| 5 | 2302 |
| 猴 | 6 |
| 全部的 | 15621 |
向我提出这个问题的戴维·菲尔默(David Filmer)其实已经知道答案了。实际上,他问的是s名水手的一般情况的公式,但我对5名水手的具体情况已经够头疼的了。戴维指出,一般情况下的答案是c = s s+1 - s + 1。
我将把这个证明留给读者。
以下是该问题替代解决方案的一些链接:
一个人收到两个装满钱的信封。其中一个信封里的钱是另一个信封的两倍。这个人选好信封,打开并清点金额后,可以选择用另一个信封换一个。问题是,换信封对这个人有什么好处吗?
由此看来,如果最初的信封金额较小,那么通过调换,该男子有50%的概率使钱翻倍;如果最初的信封金额较大,那么有50%的概率使钱减半。因此,设x为最初的信封金额,y为调换后的金额:
y = 0.5×(x/2) + 0.5×(2x) = 1.25x
假设第一个信封里有 100 美元。那么,另一个信封里有 2 × 100 美元 = 200 美元的概率是 50%,另一个信封里有 (1/2) × 100 美元 = 50 美元的概率也是 50%。在这种情况下,信封的价值为:
0.5×(100美元/2) + 0.5×(2×100美元) = 125美元
这意味着,这位男士仅仅通过交换信封,平均就能增加25%的财富!这怎么可能呢?
这看似一个数学悖论,但实际上只是对期望值公式的滥用。正如你在问题中提到的,另一个信封里的钱似乎应该比你选择的那个多25%。然而,如果你买了那个信封,那么你一开始就应该选择另一个信封。此外,如果你在决定换信封之前没有打开信封,你就可以永远用这个论点来回切换。显然,期望值论证中一定存在一些缺陷。问题是,缺陷在哪里?
这些年来,我花了很多时间阅读和讨论这个问题。我听过和读过很多关于为什么 y=.5x + .5*2x = 1.25x 的论证是错误的解释。很多人用了好几页的高等数学来解释,但我认为没有必要。这是一个简单的问题,需要一个简单的答案。所以,这是我的尝试。
你必须非常谨慎地处理这样一个事实:一个信封里的钱是另一个信封里的两倍。我们把小信封里的钱记为S,大信封里的钱记为L。这样:
长=2×小
S=0.5×L
请注意 2 和 0.5 因子是如何应用于不同信封的。您不能同时采用这两个因子并将它们应用于相同的金额。如果第一个信封中有 100 美元,那么如果是较小的信封,另一个信封中就有 200 美元。如果 100 美元是较大的信封,那么另一个信封中就有 50 美元。因此,另一个信封中有 50 美元或 200 美元。但是,您不能由此跳到说每个信封中有 50% 的概率。这是因为那样就等于将 0.5 和 2 因子应用于相同的金额,而您无法做到这一点。如果一开始就不知道奖金分配情况,您就无法将可能的金额分配给第二个信封。
如果 0.5x/2x 的论点是错误的,那么如何正确设定另一个信封的预期值呢?我会这样说:两个信封之间的差额为 LS = 2S-S = S。交换信封,你要么获得 S,要么损失 S,无论它是多少。如果两个信封分别有 50 美元和 100 美元,那么交换信封将获得或损失 50 美元。如果两个信封分别有 100 美元和 200 美元,那么交换信封将获得或损失 100 美元。无论哪种方式,交换信封的预期收益都是 0。我想我可以说,如果第一个信封有 100 美元,那么另一个信封的差额有 50% 的可能性是 50 美元,有 50% 的可能性是 100 美元。所以预期差额是 75 美元。因此,另一个信封的预期价值为 0.5×($100+$75) + 0.5×($100-$75) = 0.5×($175+$25) = $100。
希望以上信息对您有所帮助。这个问题总是会引发很多评论。如果您有意见,请不要直接写信给我,而是在我的“维加斯巫师”论坛上发帖。链接如下。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
链接
假设有一场三人决斗,参与者有A、B和C。他们为了争夺一个女人而决斗至死。他们都是绅士,并且都同意以下规则。
- 三名参与者形成一个三角形。
- 每颗子弹只有一颗。
- A 先走,然后是 B,最后是 C。
- A 击中预定目标的概率是 10%。
- B 击中预定目标的概率为 60%。
- C 击中预定目标的概率为 90%。
- 没有发生意外枪击事件。
- 允许向空中射击(故意射偏)和射击自己,并且总是成功的。
- 如果任何一轮结束后仍有两到三名幸存者,则每人获得一颗新子弹。之后,他们将按照相同的顺序轮流射击,跳过任何已经死亡的玩家。
- 三位参与者都是完美的逻辑学家。
A 最初应该瞄准谁?他针对每个初始目标的生存概率是多少?
BBC 节目《相当有趣》讨论了这个谜题。向下滚动 100 行即可查看答案和解答。
1
2
3
4
5
6
7
8
9
10
11
12
十三
14
15
16
17
18
19
20
21
22
23
24
二十五
二十六
二十七
二十八
二十九
三十
31
三十二
33
三十四
三十五
三十六
三十七
三十八
三十九
40
41
四十二
43
四十四
45
46
四十七
四十八
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
以下是我根据每个初始目标计算出的 A 获胜的概率。如你所见,故意向空中射击可以最大化 A 的获胜概率。
真实赔率
| 战略 | 概率获胜 |
| 空气 | 13.887% |
| 一个 | 0.000% |
| B | 12.560% |
| C | 13.094% |
为了解答这个问题,我们用 Pr(X) 表示一轮之后 X 组(且仅剩 X 组)存活的概率。用 Pr(X*) 表示 X 组最终赢得该轮的概率,重复此过程直至游戏状态因有人被击中而发生变化。用 Pr(X**) 表示玩家 X 是唯一幸存者的概率。为了找到最终的概率,我们先来看看两人的状态。显然,双方都会向对方射击。
A 与 B
- Pr(A) = 0.1
- Pr(B) = 0.9×0.6 = 0.54
- Pr(AB) = 0.9×0.4 = 0.36
如果两人都幸存下来,那么他们将重复这个过程,直到只剩下一个幸存者。因此,最终幸存者的概率为:
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0.1/0.64 = 0.15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0.54/0.64 = 0.84375
A 与 C
- Pr(A) = 0.1
- Pr(C) = 0.9×0.9 = 0.81
- Pr(AC) = 0.9×0.1 = 0.09
如果两人都幸存下来,那么他们将重复这个过程,直到只剩下一个幸存者。因此,最终幸存者的概率为:
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0.1/0.91 = 0.10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0.81/0.91= 0.89010989
B 与 C
- Pr(B) = 0.6
- Pr(C) = 0.4×0.9 = 0.36
- Pr(BC) = 0.$×0.1 = 0.04
如果两人都幸存下来,那么他们将重复这个过程,直到只剩下一个幸存者。因此,最终幸存者的概率为:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0.6/.96 = 0.625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0.36/.96= 0.375
现在我们来分析三人的情况。我们先来考虑一下 A 瞄准 B 的情况。
三人游戏——A 瞄准 B
如果A击中B,那么C肯定能幸存,但可能击中A,也可能击不中。因此,击中B的两种可能结果是AC和C。如果A击中B未击中,那么B会瞄准威胁更大的C。如果B击中C,那么A和B都能幸存。如果B击中C未击中,那么C会瞄准威胁更大的B。如果C击中B未击中,那么A和C都能幸存。如果C击中B,那么A和C都能幸存。因此,可能的结果是C、AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0。
- Pr(C) = 0.1 × 0.9 = 0.09。这是通过 A 击中 B,然后 C 击中 A 实现的。
- Pr(AB) = 0.9 × 0.6 = 0.54。这是通过 A 击中 B,然后 B 击中 C 实现的。
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334。这可以通过两种方式实现。第一种是 A 命中 B,然后 C 未命中 A。第二种是 A 未命中 B,B 未命中 C,然后 C 命中 B。
- Pr(BC) = 0。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。这是通过三项全部缺失实现的。
按照与双人情况相同的逻辑,我们可以将每个结果除以 (1-Pr(ABC))=0.964 来找到每个状态的概率,假设游戏状态在回合之后确实发生了变化。
- Pr(C*) = 0.09/0.964 = 0.093361。
- Pr(AB*) = 0.54/0.964 = 0.560166。
- Pr(AC*) = 0.334/0.964 = 0.346473。
从双人对决的情况来看,如果是A和B,那么A获胜的概率为0.15625,B获胜的概率为0.84375。如果是A和C,那么A获胜的概率为0.109890,C获胜的概率为0.890110。
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600。A 可以通过两种方式获胜:(1) 进入 AB 状态,然后获胜;(2) 进入 AC 状态,然后获胜。
- Pr(B**) = 0.560166 × 0.84375 = 0.472640。如果B进入AB状态,则B获胜,B为胜者。
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760。C 可以通过 A 杀死 B,然后 C 在第一轮杀死 A 来获胜,或者通过进入状态 AC,然后 C 获胜。
因此,如果 A 的策略是首先瞄准 B,那么他成为唯一幸存者的概率是 12.56%。
三人游戏——A 瞄准 C
如果A击中C,那么B肯定会幸存,但可能会击中A,也可能不会。因此,击中C的两种可能结果是AB和B。如果A没有击中C,那么B会瞄准威胁更大的C。如果B击中C,那么A和B都会幸存。如果B没有击中C,那么C会瞄准威胁更大的B。如果C没有击中B,那么A和B都会幸存。如果C击中B,那么A和C都会幸存。因此,可能的结果是B、AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0.1 × 0.6 = 0.06。
- Pr(C) = 0。
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58。这可以通过两种方式实现。第一个是 A 击中 C,然后 B 击中 A。第二个是 A 击中 B,然后 B 击中 C。
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324。这是通过 A 缺失 C、B 缺失 C 以及 C 命中 B 实现的。
- Pr(BC) = 0。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。这是通过三项全部缺失实现的。
按照与双人情况相同的逻辑,我们可以将每个结果除以 (1-Pr(ABC))=0.964 来找到每个状态的概率,假设游戏状态在回合之后确实发生了变化。
- Pr(B*) = 0.06/0.964 = 0.062241。
- Pr(AB*) = 0.58/0.964 = 0.601660。
- Pr(AC*) = 0.324/0.964 = 0.336100。
按照与 A 针对 B 的情况的解决方案相同的逻辑:
- Pr(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943。
- Pr(B**) = 0.062241 + 0.601660 × 0.84375 = 0.569891。
- Pr(C**) = 0.336100 × 0.890110 = 0.299166。
因此,如果 A 的策略是首先瞄准 C,那么他成为唯一幸存者的概率是 13.09%。
三人 — A 故意失手
A故意射偏后,B会瞄准威胁更大的C。如果B击中C,A和B都会幸存。如果B射偏C,C会瞄准威胁更大的B。如果C射偏B,A和B都会幸存。如果C射偏B,A和C都会幸存。因此,可能的结果是AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0。
- Pr(C) = 0。
- Pr(AB) = 0.6。这是通过 B 击中 C 实现的。
- Pr(AC) = 0.4 × 0.9 = 0.36。这是通过 B 未命中 C,然后 C 命中 B 实现的。
- Pr(BC) = 0。
- Pr(ABC) = 0.4 × 0.1 = 0.04。这是通过全部三个缺失来实现的。
按照与双人情况相同的逻辑,我们可以将每个结果除以 (1-Pr(ABC))=0.96 来找到每个状态的概率,假设游戏状态在回合之后确实发生了变化。
- Pr(AB*) = 0.6/0.96 = 0.625。
- Pr(AC*) = 0.36/0.96 = 0.375。
按照与 A 针对 B 的情况的解决方案相同的逻辑:
- Pr(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865。
- Pr(B**) = 0.625 × 0.84375 = 0.527344。
- Pr(C**) = 0.375 × 0.890110 = 0.333791。
因此,如果 A 的策略是首先瞄准 C,那么他成为唯一幸存者的概率是 13.89%。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
一次比较两个元素,对列表进行排序的最快方法是什么,从而最大限度地减少比较次数?
有几种方法效果差不多。不过,我发现最容易理解的方法是合并排序。它的工作原理如下:
- 将列表一分为二。继续将每个子集再分成两部分,直到每个子集的大小都为 1 或 2。
- 对 2 的每个子集进行排序,将较小的成员放在最前面。
- 将子集对合并在一起。不断重复,直到只剩下一个排序好的列表。
合并两个列表的方法是比较每个列表的第一个成员,并将较小的一个放入一个新列表中。然后重复此操作,将较小的一个放在上一次比较的较小成员之后。不断重复此操作,直到两组合并为一个有序组。如果原始列表之一为空,则可以将另一个列表附加到合并后列表的末尾。
下表显示了根据列表中元素的数量所需的最大比较次数。
合并排序
| 元素 | 最大比较数 |
| 1 | 0 |
| 2 | 1 |
| 4 | 5 |
| 8 | 17 |
| 16 | 49 |
| 三十二 | 129 |
| 64 | 321 |
| 128 | 769 |
| 256 | 1,793 |
| 512 | 4,097 |
| 1,024 | 9,217 |
| 2,048 | 20,481 |
| 4,096 | 45,057 |
| 8,192 | 98,305 |
| 16,384 | 212,993 |
| 32,768 | 458,753 |
| 65,536 | 983,041 |
| 131,072 | 2,097,153 |
| 262,144 | 4,456,449 |
| 524,288 | 9,437,185 |
| 1,048,576 | 19,922,945 |
| 2,097,152 | 41,943,041 |
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
2010年10月29日, 《拉斯维加斯评论报》刊登了一项关于里德和安格尔参议员竞选的民意调查。调查显示,在对625名潜在选民的调查中,安格尔的得票率为49%,里德的得票率为45%。调查还显示,误差幅度为4%。以下是我的问题:
- Angle 获胜的概率是多少?
- Angle 的得票率的 95% 置信区间是多少?
- 误差幅度是什么意思?
抱歉,回复得有点过时。以下是我在选举前写的。
首先,我要剔除剩下的6%,他们要么犹豫不决,要么会把选票浪费在第三方候选人身上,或者“以上皆非”(在内华达州,这两者是可以考虑的)。有些人可能不同意这个假设。说实话,忽略他们的另一个原因是,如果候选人超过两位,计算起来会更加复杂。所以,四舍五入后,安格尔有306票,里德有281票,样本总数为587票。
我将使用标准正态近似来回答这个问题。如果我是一个完美主义者,那么我会使用T分布,因为实际的均值和方差是未知的。然而,在我看来,对于正态分布来说,587的样本量是完全可以接受的。
样本量 = 306+281 = 587。
角度样本平均值为 306/587 = 0.521295。
平均值的估计标准差为 (0.521295 × 0.478705 / (587-1))^0.5 = 0.0206361。
Angle 的 50% 以上的份额为 (0.521295-0.5)/0.0206361 = 1.031917 个标准差。
根据正态分布,Reid 最终结果超出预期 1.031917 个标准差的概率为 0.151055。这可以在 Excel 中使用函数 NORMSDIST(-1.031917) 计算得出。因此,Angle 获胜的概率为 1-0.151268 = 84.89%。
要创建 95% 的置信区间,请注意高斯曲线两侧 2.5% 的点与平均值之间的标准差为 1.959964。这可以在 Excel 中使用函数 NORMSINV(0.975) 计算得出。如前所述,样本平均值的估计标准差为 0.0206361。因此,两位候选人的得票率与民调结果之间的标准差在 0.0206361×1.959964 = 0.040446 以内的可能性为 95%。因此,Angle 的 95% 置信区间为 0.521295 +/- 0.040446 = 48.08% 至 56.17%。
有人告诉我,如果这样表述在数学上是不正确的:“Angle在所有Angle/Reid选票中的份额有95%的可能性落在48.08%到56.17%之间。” 我最初的回答就是这样的,但两位统计学家对我的措辞感到震惊。解释一下他们的回答,他们说我必须使用被动语态,说“48.08%和56.17%将以95%的概率围绕Angle的份额”。 说实话,在我看来,这听起来是一样的。然而,他们强调置信区间是随机的,而Angle的份额是不可改变的,而我最初的措辞暗示了相反的意思。无论如何,我希望频率统计专家们会对第二种表述感到满意。
“误差幅度”是95%置信区间两端差值的一半。在本例中,(56.17% - 48.08%)/2 = 4.04%。
作为后续,以下是实际结果:
里德:361,655
角度:320,996
其他:21,979
因此,不计入“其他”选票,里德获得了53.0%的选票,安格尔获得了47.0%的选票。里德轻松赢了6%。这不禁让人思考,民调结果为何如此悬殊。是偶然吗?选民改变了主意吗?还是民调结果本身就很糟糕?我把这些问题留给读者去思考(我讨厌教科书上这么说)。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
我试用了你们的精算计算器。为什么我达到预期死亡年龄的概率不到 50%?
你混淆了平均值和中位数。我们以我的情况为例。我是一名45岁的男性。我的预期寿命是78.11岁,但我活到80岁的概率是50.04%。
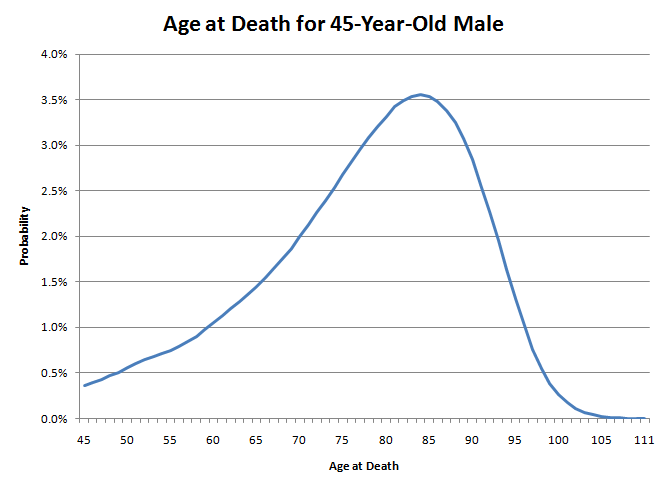
我的死亡年龄就像向这张图投掷飞镖一样。注意左尾比右尾粗得多。这意味着我现在死亡的概率很低。然而,随着年龄的增长,明年死亡的概率会越来越高。例如,对于一个45岁的男性来说,活到46岁的概率相当高,达到99.64%。然而,到了85岁,活到86岁的概率只有89.21%。这就像大自然慢慢地在你的背后捅刀子。起初它可能不会杀死你,但随着时间的流逝,它杀死你的概率会慢慢增加。然而,一旦你到了七十多岁后期,大自然就会对你不再玩命,开始真正地捅刀子。
因此,如果许多45岁的男性向这张图投掷飞镖,49.96%的人将在45岁至79岁之间命中,50.04%的人将在80岁至111岁之间命中。然而,幸运地落在图表右侧的那一半人可能活不过80岁。男性一旦达到80岁,预期寿命也只有7.78年。与此同时,那些不幸活不到80岁的人,许多人的寿命会比80岁短得多。因此,正是大量年轻人的死亡拉低了平均预期寿命。
对于类似的情况,考虑一个数字为 10、20、30、31、32、33 的骰子。平均值是 26,但掷出大于该值的概率为 2/3。
举个例子来说明平均值和中位数的不同之处,假设我们在样本中再增加两个死亡病例。一个在46岁时死亡,另一个在81岁时死亡。活到80岁的概率保持不变,但45岁时的平均预期寿命会下降。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
想象一条无限弹性的橡皮筋,未拉伸时长1公里。它以每秒1公里的速度膨胀。接下来,想象橡皮筋的一端有一只蚂蚁。当橡皮筋开始膨胀时,蚂蚁以相对于当前位置每秒1厘米的速度向另一端爬行。蚂蚁最终会到达另一端吗?如果会,什么时候?
是的, 100,000 -1秒后就会了。请参阅我的mathproblems.info网站,问题 206,其中有两个答案。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
你认为更高的燃油效率值得你额外花点钱买一辆混合动力车吗?你需要开多少英里才能收支平衡?
问得好。为了回答这个问题,我考虑了一辆丰田汉兰达,我正在考虑购买。标准混合动力车型的零售价为37,490美元。同一款四轮驱动车型,非混合动力车型的零售价为29,995美元。所以,混合动力车型的成本增加了7,495美元。
混合动力车型的油耗为28英里/小时(市区和高速公路)。非混合动力车型的油耗分别为17英里/小时(市区)和22英里/小时(高速公路)。我们取平均值19.5英里/小时。
盈亏平衡里程数的一般公式为 h×m h ×m r /(g×(m h -m r )),其中
h = 混合的额外成本。
g = 一加仑汽油的成本。
m r = 非混合动力汽车的里程(“r”代表普通汽车)。
m h = 混合动力汽车的里程数。
下表使用此公式来查找每加仑 2 美元至 5 美元的各种汽油价格的盈亏平衡点。
混合盈亏平衡点
| 天然气成本 | 英里数 |
| 2.00 美元 | 240,722 |
| 2.25 美元 | 213,975 |
| 2.50 美元 | 192,577 |
| 2.75 美元 | 175,070 |
| 3.00 美元 | 160,481 |
| 3.25 美元 | 148,136 |
| 3.50 美元 | 137,555 |
| 3.75 美元 | 128,385 |
| 4.00 美元 | 120,361 | 4.25 美元 | 113,281 |
| 4.50 美元 | 106,987 |
| 4.75 美元 | 101,357 |
| 5.00 美元 | 96,289 |
因此,按照拉斯维加斯目前每加仑3美元的油价计算,您需要行驶超过160,481英里才能获得更高的燃油经济性。这还不包括混合动力汽车可能带来的其他费用,例如昂贵的电池更换成本,以及任何因减少化石燃料消耗而产生的环保积分。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
除了同卵双胞胎之外,我与同胞兄弟姐妹的基因有多少比例是相同的?
1/2。
如果我们用基诺彩票来类比,每个人都有40个基因,每个基因都代表一个基诺球。然而,每个球都有唯一的编号。当两个没有血缘关系的人交配时,就像把他们两人的80个球组合成一个漏斗,然后随机选择40个基因作为交配后代的基因。
所以,当你受孕时,你得到了一半的彩球,另一半则被浪费了。当你的兄弟姐妹受孕时,他/她得到了你出生时抽取的彩球的一半,以及另一半未被抽取的彩球。所以,你们的基因有50%是相同的。这和基诺彩票如果抽取40个号码,连续两次抽取平均会有20个相同的彩球的原因是一样的。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
一家生产桌椅的工厂配备了10台锯、6台车床和18台砂光机。制作一把椅子需要锯10分钟、车床5分钟和砂光5分钟才能完成。制作一张桌子需要锯5分钟、车床5分钟和砂光20分钟才能完成。一把椅子售价10美元,一张桌子售价20美元。工厂每小时应生产多少张桌椅才能获得最高收益?收益是多少?
设c代表每小时制作的椅子数量,t代表桌子数量。每小时收入为10×c + 20×t。
10把锯子每小时锯600分钟。已知一把椅子锯10分钟,一张桌子锯5分钟。因此,每小时产量限制为:
(1)10c + 5t <= 600
6台车床每小时加工时间共计360分钟。我们已知,锯一把椅子需要5分钟,锯一张桌子需要5分钟。因此,每小时产量限制为:
(2)5c + 5t <= 360
18台砂光机每小时可进行1080分钟的砂光作业。我们假设一把椅子需要锯5分钟,一张桌子需要锯20分钟。因此,每小时的产量限制为:
(3)5c + 20t <= 1080
下图显示了三组机器所施加的三个约束。工厂可以生产符合所有三条线的任意椅子和桌子组合。问题是,在三条线下,哪个组合能带来最大的收益。
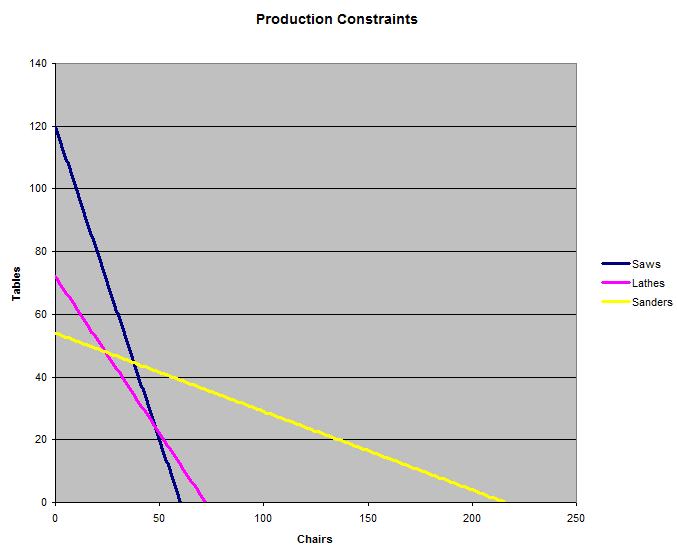
按理说,答案应该是两条线的交点、所有椅子或所有桌子。那么,让我们找出这两条线的交点。首先,让我们找出公式 (1) 和公式 (2) 的交点。我们可以将 <= 表达式改为 =,以最大限度地发挥机器的潜力。
(1)10美分+5吨=600
(2)5c + 5t = 360
从 (1) 中减去 (2):
5美分=240
c = 48
将 48 代入公式 (1) 中,得到 c:
10×48 + 5t = 600
5t = 120
t = 24
因此,等式 (1) 和 (2) 在 48 把椅子和 24 张桌子处相交。
接下来,让我们找出方程 (2) 和 (3) 的交点:
(2)5c + 5t = 360
(3)5c + 20t = 1080
从 (3) 中减去 (2):
15吨=720
t = 48
将其代入 (2) 或 (3) 中,我们可以解出 c,即 24。
因此,等式 (2) 和 (3) 在 24 把椅子和 48 张桌子处相交。
我们不需要费心寻找方程 (1) 和 (3) 的交点,因为我们可以从图中看到锯线和砂光机线的交点在车床约束之外。
也可能只做椅子才是正确答案。图表显示,锯子是只做椅子的最大限制因素。根据公式 (1),如果我们将桌子数量代入 0,则 c=60。
另一种可能性是只做桌子。图表显示,砂磨机将是最大的限制因素。将0把椅子代入公式(3),我们发现最多只能做54张桌子。
下图显示了每个可行答案的总收入。记住,每把椅子的收入是10美元,每张桌子的收入是20美元。
每小时总收入
| 椅子 | 表格 | 收入 |
| 0 | 54 | 1,080美元 |
| 24 | 四十八 | 1,200美元 |
| 四十八 | 24 | 960美元 |
| 60 | 0 | 600美元 |
国王有一桶满满的酒。
星期一晚上,一个仆人从桶里偷走了三个杯子,并用三杯水代替。
周二晚上,另一个仆人从已经稀释的酒桶中偷走了三杯酒,并用三杯水代替。
星期三晚上,又有一个仆人从已经稀释的酒桶里偷走了三杯酒,并用三杯水代替。
周四早上,酒桶里 50% 是酒,50% 是水。
桶里最初有多少酒?
这是答案和解决方案(PDF)。
有关此问题的讨论,请访问我在Wizard of Vegas 的论坛。
如果我有一碗200颗彩虹糖,其中3颗就能杀死我,那么如果我抓起12颗彩虹糖并全部吃掉,我死亡的概率是多少?假设只需要一颗有毒的彩虹糖就能杀死我。
答案是 1-combin(197,12)/combin(200,12) = 17.02%。
有关此问题的更多讨论,请访问我在Wizard of Vegas 的论坛。
一个外星人绑架了十位逻辑学家,并把他们关在一个房间里。他向他们解释说,他首先把他们排成一排,从高到矮,每个人都面向前面第二矮的人,这样每个人都能看到所有矮个子的逻辑学家,但看不到更高的逻辑学家。然后他解释说,他会给每个人戴上一顶黑色或白色的帽子,但没有人能看到自己帽子的颜色,只能看到矮个子逻辑学家的帽子。黑白帽子的分布可以是任意的,不一定是五顶五顶。
外星人随后解释说,他会从最高的开始,依次询问每位逻辑学家帽子的颜色。逻辑学家可以听到前面人的回答。除了黑白答案外,游戏开始后,他们不得以任何方式交流。如果超过一位逻辑学家答错,他们就会被全部吃掉。如果至少有九个答案正确,他们将被安全送回地球。然后,外星人会给他们一些时间制定策略。他们的策略应该是什么?
以下是一种可行的策略。让第一个行动的逻辑学家,如果看到其他九位逻辑学家戴的帽子数量为偶数,就说“黑色”,如果看到其他九位逻辑学家戴的帽子数量为奇数,就说“白色”。他有50%的概率匹配自己帽子的颜色,所以他是唯一一个可以犯错的人。无论他说了什么,都将其定义为“运行颜色”。
接下来,第二位行动的逻辑学家将计算较矮的八位逻辑学家的黑帽数量,并用与第一位逻辑学家相同的奇偶方法将其与颜色匹配。如果结果与第一位逻辑学家给出的颜色一致,那么他一定戴着白帽,并应选择白色。如果结果不一致,那么他一定戴着黑帽,并应选择黑色。如果他说“白色”,则当前颜色保持不变。如果他说“黑色”,则当前颜色将翻转为相反的颜色。
接下来,第三位逻辑学家的操作与第二位完全相同,但会数一下其他七位较矮的逻辑学家手中的黑帽数量。同样,如果他同意当前颜色,他会说“白色”,当前颜色保持不变。如果他不同意当前颜色,他会说“黑色”,当前颜色将翻转。
其他逻辑学家也会做同样的事情。
当然,他们也可以很容易地将黑色与奇数联系起来,将白色与偶数联系起来。重要的是,他们都同意哪种颜色代表哪种奇偶校验。无论采用哪种策略,都会导致第二到第十位逻辑学家认为所有答案都正确,而第一位逻辑学家有50%的概率活下来。这个策略适用于任何数量的逻辑学家。
阿克塞尔和鲍勃各自有一副52张的牌。两人都随机洗牌。然后,他们同时从每副牌中翻出一张牌。他们同时翻出同一张牌至少一次的概率是多少?
答案很容易估算为 1-(51/52) 52 = 0.63568648。然而,估算在智力上实在难以令人满意。所以,让我们来求一个精确的解吧!
步骤 1:首先,考虑第二副牌的排序方式数,其中第一张牌是 1。答案是排序其他 51 张牌的方式数,即 51!= 1551118753287382280224243016469303211063259720016986112000000000000。
任何牌都能匹配第一副牌,所以我们必须对所有 52 张牌都进行同样的操作。这样一来,就有 52*51! = 52! 种组合,其中至少有一张牌匹配。
步骤 2:然而,步骤 1 会重复计算两张牌匹配的所有情况。例如,如果前两张牌是 1 和 2,那么我们需要将其他牌的 50! 种排列方式计算两次,第一次将 1 作为第一张牌,第二次将 2 作为第二张牌。从 52 张牌中选择 2 张牌的方式数为 combin(52,2) = 1326。对于每两张牌的组合,其他牌的排列方式有 50! = 3041409320171337804361260816606476884437764156896051200000000000000 种。因此,对于步骤 2,我们需要减去 combin(52,2)*50! = (52*51/2!)*50! = 52!/2! 种组合。
步骤 3:接下来,考虑随机牌堆中前三张牌的顺序为 1、2 和 3 的情况。其余 49 张牌有 49! 种排序方法。在初始步骤中,我们会数三次,以找出至少一张匹配的牌。然后,在第二步中,我们会减去所有 combin(3,2)=3 种从这三张牌中选择 2 张的方法。因此,这种情况会被计算 3-3=0 次,因此我们需要将它们加回去。有 combin(52,3) 种选择至少 3 张匹配牌的情况。因此,我们需要重新添加 combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! 种组合。
步骤 4:接下来,考虑随机牌堆中前四张牌的顺序为 1、2、3 和 4 的情况。其余 48 张牌有 48! 种排序方法。在初始计数至少一张匹配牌的步骤中,我们需要数四次。然后,在步骤 2 中,我们需要减去所有 combin(4,2)=6 种从这四张牌中选择两张的方法。然后,我们需要加上所有 combin(4,3)=4 种从这四张牌中选择三张的方法。因此,每种情况都有 4-6+4=2 种计数方法。因此,我们需要减去其中一种计数方法,使每种情况都只计算一次。共有 combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! 种需要加回去的情况。
我们将继续这样做,交替进行加法和减法来纠正重复计算。
最后,随机牌堆中至少有一张牌与有序牌堆匹配的情况数量 = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783。
共有 52 种方法可以排列 52 张牌!= y = 5271776154963652194226185415451226599692124538619822080000000000000 种方法可以排列 52 张牌。
因此,答案是 x/y = 0.6321205588285576784044762298
没有匹配的概率是 1-(x/y) = 0.3678794411714423215955237702。
如果这个数字看起来很熟悉,那就对了。1/e = 0.3678794411714423215955237702。
因此,答案可以非常接近地估计为 1-(1/e)。
致谢
数学计算是在Pari/GP中进行的
这个问题已在我的Wizard of Vegas论坛中提出并讨论过。
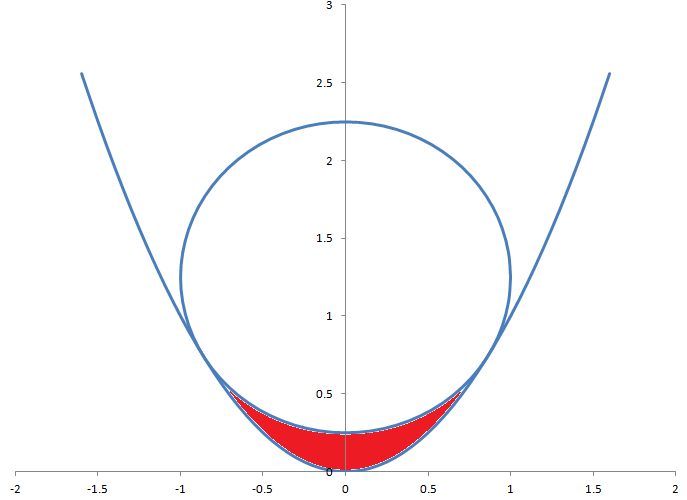
半径为 1 的圆与方程 y=x 2的抛物线相切。圆与抛物线之间的红色区域面积是多少?
点击下面的按钮获取答案。
这是我的解决方案。(PDF)
我在Wizard of Vegas论坛上提出并讨论了这个问题。
我从Mind Your Decisions的 Presh Talwalker 那里遇到了这个问题。
一位赌场荷官正在研究一种新的三张牌扑克游戏。她从一副标准牌中取出所有人头牌,并彻底洗牌。然后,她给玩家1发了3张牌,给玩家2发了3张牌,给玩家3发了3张牌,最后给玩家4发了3张牌。四手牌中都包含顺子(任意花色的JQK)的概率是多少?

[剧透=解决方案]
第一手牌是AKQ的概率是1*(8/11)*(4/10) = 29.09%。
假设第一手牌已经是 AKQ,那么第二手牌是 AKQ 的概率等于 1*(6/8)*(3/7) = 32.14%。
假设第一和第二手牌都是 AKQ,那么第三手牌是 AKQ 的概率等于 1*(4/5)*(2/4) = 40.00%
由于前三手牌都是AKQ,所以剩下的牌一定是AKQ。因此,概率是上述三个概率的乘积,即216/5775 = 约0.037402597。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
随机内接于半径为 1 的圆的矩形的平均面积和周长是多少?
好问题。以下是我的答案:
这是我对这两个问题的解决方案(PDF)。
找到一个十位数,满足:
- 该数字的第一位数字是整个数字中 0 的个数。
- 该数字的第二位数字是整个数字中 1 的个数。
- 该数字的第三位数字是整个数字中 2 的个数。
- 该数字的第 4 位数字是整个数字中 3 的个数。
- 该数字的第 5 位数字是整个数字中 4 的数量。
- 该数字的第 6 位数字是整个数字中 5 的数量。
- 该数字的第 7 位数字是整个数字中 6 的数量。
- 该数字的第 8 位数字是整个数字中 7 的数量。
- 该数字的第 9 位数字是整个数字中 8 的数量。
- 该数字的第 10 位是整个数字中 9 的个数。
[spoiler=答案]6,210,001,000[/剧透]
我在Wizard of Vegas论坛上提出并讨论了这个问题。
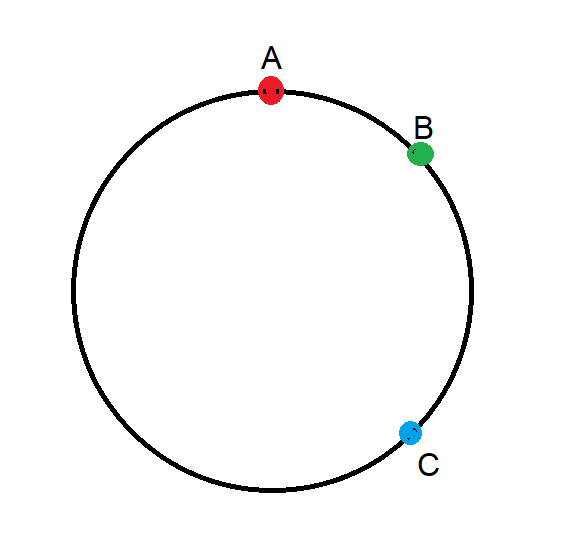
三个点随机均匀地分布在半径为 1 的圆上。沿圆周测量距离时,这三个点之间的预期最小距离是多少?
爱丽丝和比尔花了 3 个小时粉刷一栋房子。
爱丽丝和辛迪花了 4 个小时粉刷一栋房子。
比尔和辛迪花了 5 个小时粉刷一栋房子。
如果全部都画的话需要多长时间?
[spoiler=答案]120/47 =~ 2.553191 小时[/剧透]
这是我的解决方案(PDF)。


