概率 - 一般问题
您的意思是,从长远来看,无论您做什么,您都会在每场赌场游戏中输钱吗?
除了二十一点和视频扑克中罕见的正期望机会外,是的,这就是我所说的。
我怎样才能将您的概率转换为 x 到 y 格式?
假设某事发生的概率为 x 比 y,意味着该事件每不发生 y 次,就会发生 x 次。为了进行转换,设 p 为某事发生的概率。该概率也可以表示为 (1/p)-1 比 1。让我们看一个例子。在五张牌梭哈中抽到葫芦的概率是 0.00144058。这也可以表示为 693.165 比 1。
我最近看到⾜球的赌盘总⾦额。其形式为100个⽅框的格线、沿着X与Y轴 线并且有0-9回合、对应最后的⽐赛分数。我并不是⾜球迷、也从未押注 这样的赌盘, 不过我是⼀位赌客, 并且不认为这是很好的押注。 我认为你应该知道我所提出的这种型态。每⼀个⽅框花费$5、并且在每⼀ 个quarter场次⽀付。如果你的⽅框赢了、你就赢到$125、并且有可能赢 到所有的4个quarters场次, 如果最后的次数保持相同、则针对100⽐1的⽀ 付赔率⽽赢到$500. 对我推销这款押注的⼈试着告诉我, 赢到$500的概率是100⽐1. 我并不认 同。⾸先, ⽅框俱有0 + 7较⾼的赢注机会、相较于2 + 9的⽅框。然⽽, 0 + 7的概率整场⽐赛维持最后2个次数必须是⾼的。如果⽅框是透过随机⽅式 来帮你选定, 你能否告诉我赢到$500奖⾦的⼤约概率是多少?
假设格线当中的⽅框栏位是由随机选出的, 那么在任何⼀个quarter场次赢 的概率将会是1/100. 假设每⼀个quarter场次都是独⽴事件, 其实并⾮如此, 赢到所有四个quarters场次的概率将会是 (1/100)4 = 100百万分之⼀。
我真的很想知道如何解读像 12 比 1 或 3 比 2 这样的赔率。哪一个赔率显示获胜的几率最高?12 比 1 还是 3 比 2?
我不喜欢用这种形式的概率,但它们通常用在这样的句式中:“抽到同花大顺的概率是649,739比1。” 这意味着有649,739种方法你抽不到同花大顺,只有1种方法可以抽到。在你的例子中,12比1的概率是1/13,即7.69%,而3比2的概率是2/5,即40.00%,所以3比2的概率更高。
在《圣路易斯邮报》的一篇文章中,记者写道:“五百年一遇的洪水是指每年发生概率为五百分之一的洪水。换句话说,就是50年内发生的概率是十分之一,一个世纪内发生的概率是五分之一。” 读完你所有的赌博页面后,我觉得这样的说法不太对,对吧?按照他们的说法推断,这意味着每500年发生一次洪水的概率是一分之一,这不可能是对的。
你说得对,那篇文章是错误的。在 x 年的时间段内发生五百年一遇洪水的概率是 1-e -x/500 。因此,50 年内至少发生一次五百年一遇洪水的概率是 9.52%,100 年内至少发生一次五百年一遇洪水的概率是 18.13%。
如果我确定一场比赛的公平线是-160/+160,而我发现一条-145的恶意线,我的期望值是多少?如果您能提供任何公式,让我在公平线确定后推导出我的期望值+/-,我将不胜感激。
设 p 为热门球队获胜的概率。如果 -160 为公平赔率,则:
100*p-160*(1-p)=0
260便士=160
p = 160/260 = 8/13 = 61.54%。
因此,在赔率为-145的赔率线上,下注145美元的预期回报为(8/13)*100 + (5/13)*-145 = 75/13 = 5.77美元。因此,玩家优势为5.77美元/145美元 = 3.98%。
我们将t定义为不计庄家优势的真实赔率线,a定义为实际赔率线。以下是玩家预期回报的公式:
A 为负数,t 为负数:(100*(ta) / (a*(100-t))
A为正,t为正:(at)/(100+t)
A 为正数,t 为负数:(a*t + 10000)/((t-100)*100)
因此,在您的情况下,您的预期回报率是 100*(-160 -(-145))/(-145*(100-(-160))) = 3.98%。
您如何看待下面的说法:上帝是民主党人,因为 2000 年投票支持戈尔的所有县都没有受到最近袭击佛罗里达州的三次飓风的影响?
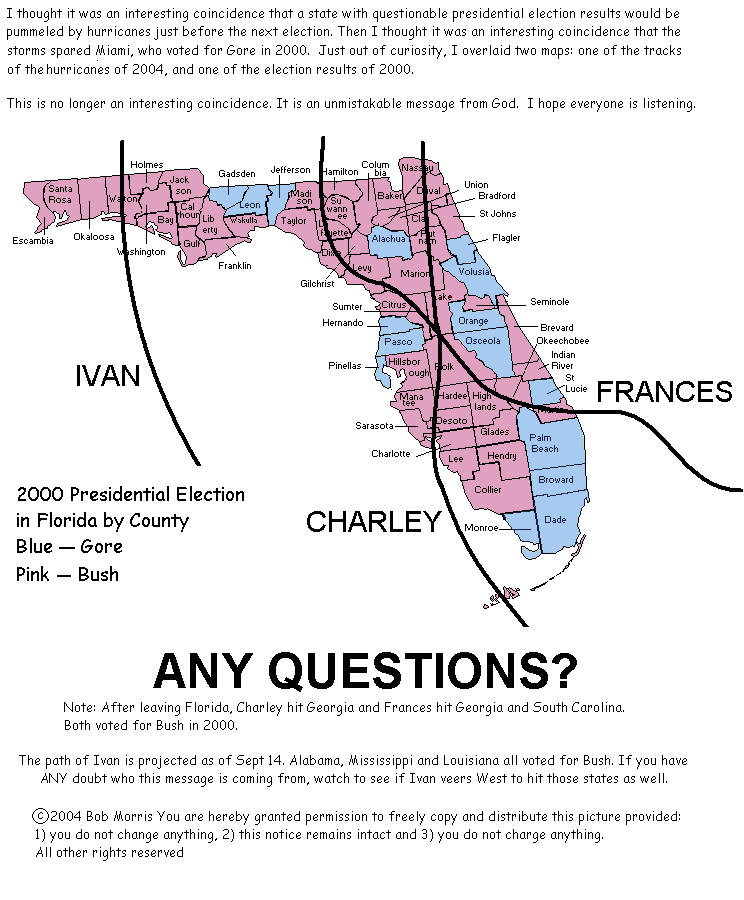
首先,我之所以发表这篇文章,是因为作者在文章底部允许我这么做。这是一个很好的例子,说明相关性并不一定意味着因果关系。回顾过去,很容易发现很多巧合。要论证任何事,都应该在收集任何证据之前先提出假设。
后续(2004年11月13日):另一位读者指出,这张地图最初只是个玩笑,后来却成了都市传说。正如此链接指出的那样,图中的飓风路径根本不准确,而且实际飓风袭击了戈尔县的许多县。这恰恰表明,你不应该轻信你读到的一切,尤其是在互联网上。
我觉得你可能会觉得这很有趣。博狗(Bodog)提供这样一个赌注:“布兰妮·斯皮尔斯和凯文·费德林的第二个孩子是男孩还是女孩?” 男孩的赔率是+105,女孩的赔率是-145。我上次查的时候,自人类诞生以来,这个赔率一直是1:1。我想知道谁会押-145。我喜欢这个网站,经常访问,并点击你的赞助商以表感谢。
谢谢你的赞美。说实话,现在没人太在意点击率了。所以,如果只是为了炫耀,就没必要非得点开横幅广告。回答你的问题,在美国,生男孩的概率非常接近50.5%,生女孩的概率接近49.5%。假设博彩界没有其他信息,那么押注男孩的玩家优势应该是0.505*1.05 - 0.495 = 3.53%。也可能是掌握内幕消息的人押注女孩。另一种说法是,有些人错误地认为可以通过母亲的肚子形状来判断性别,而这些人押注的是女孩。我个人不去深究这个问题。
在这段YouTube视频中,马特·达蒙称约翰·麦凯恩有三分之一的几率无法撑过第一任期。他是对的吗?
不是。根据美国疾病控制与预防中心 (CDC) 的精算表,72 岁的白人男性活到 76 岁的概率为 85.63%。这意味着死亡概率约为七分之一。存活率可以通过将 76 岁时出生队列的 57,985 人除以 72 岁时出生队列的 67,719 人得出,该数据来自第 14 页的白人男性表格。使用的表格称为“周期生命表”,它假设 2003 年的死亡率在未来不会发生变化,这是最常用的精算表类型。追求完美的人可能会想使用 1936 年的队列生命表,但我认为这不会有太大区别。
附言:发布此回复后,我收到几条评论,说我的回复没有考虑到约翰·麦凯恩的个人健康状况。他的不利之处在于他是一名癌症幸存者。他的优势在于能够享受到金钱能买到的最好的医疗服务,对于一个72岁的老人来说,他的身心状态显然仍然很好,而且长寿,他的母亲仍然健在就是明证。然而,我从未打算将这些信息考虑在内。我指的是马特·达蒙引用的精算表。我只是说,对于普通的72岁白人男性来说,再活四年的概率是86%。如果必须的话,我预测约翰·麦凯恩的几率甚至会更高。
给定等量的纸,哪个纸杯能装更多的水?圆柱形还是锥形?假设圆柱的一端开口,且两种形状的尺寸都是最优的。
请参阅我的配套网站MathProblems.info ,问题编号 210,以获取答案和解决方案。
你听说过新泽西州爆米花公园动物园里的骆驼公主的故事吗?它在NFL让分盘口中取得了88胜51负的战绩。它的赔率是多少?
不计入平局,在139次选择中至少赢得88次的概率是0.00107355,也就是931分之一。这真是令人失望。我敢肯定,还有930只动物的表现更差,只是没人提及而已。想了解更多关于“公主”的信息,请阅读ESPN.com上的文章《新泽西骆驼预测巨人队战胜爱国者队》 。
在2012年5月8日的《切尔西晚间秀》节目中,切尔西说红头发的猫正在逐渐消失,因为它们彼此之间不交配。这是真的吗?
我希望你开心;我为此花了好几个小时。
要回答这个问题,重要的是量化切尔西·汉德勒“红头假说”下的行为。以下是我的假设。
- 红头发的人永远不会与另一个红头发的人交配。
- 雌性总是会选择雄性进行交配。
- 每个人都会交配,每次交配都会产生相同数量的孩子。
- 红头发的雌性动物将有优先选择配偶的权利,在非红头发的动物中随机选择。
- 女性携带者(拥有一个红发基因)将在红头发剩下的男性中随机选择配偶。
- 阴性女性(既没有红发基因)将在红发男性和携带者剩下的男性中随机选择。
根据“今天我发现了”的数据,我首先假设红头发的概率是 4%。然后我假设在此之前,人们对红头发没有偏见。
假设对红头发的偏见从下一代开始,并持续下去,那么总体人口中红头发的趋势会是怎样的呢?我做了大量电子表格(我就不细说了),以下是从这一代开始的前八代数据。
红头发比例
| 一代 | 部分 |
|---|---|
| 1 | 4.000000% |
| 2 | 3.888889% |
| 3 | 3.895219% |
| 4 | 3.894863% |
| 5 | 3.894883% |
| 6 | 3.894882% |
| 7 | 3.894882% |
| 8 | 3.894882% |
我们看到的是,到第三代,红头发人口的比例将收敛到3.90%。所以,不管切尔西怎么说,我认为红头发的人没什么可担心的。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
据CardPlayer.com报道,阿米尔·莱哈沃特(Amir Lehavot)是九位进入 2013 年世界扑克锦标赛决赛桌的选手之一,他将以每 1% 份额 29,248 美元的价格出售第九名的奖金,这些奖金超过了最低奖金 733,224 美元。这个价格合理吗?
首先,让我们回顾一下筹码堆栈。
2013 WSOP 决赛桌筹码量
| 玩家 | 薯片 |
|---|---|
| 陈俊杰 | 38,000,000 |
| 阿米尔·莱哈沃特 | 29,700,000 |
| 马克·麦克劳克林 | 26,525,000 |
| 杰伊·法伯 | 25,975,000 |
| 瑞安·里斯 | 25,875,000 |
| 西尔万·卢斯利 | 19,600,000 |
| 米歇尔·布鲁梅尔豪斯 | 11,275,000 |
| 马克·纽豪斯 | 7,350,000 |
| 大卫·贝内菲尔德 | 6,375,000 |
下表显示了锦标赛中每场最终比赛的胜利情况。
2013年WSOP决赛桌奖金
| 地方 | 赢 |
|---|---|
| 第一 | 8,359,531美元 |
| 第二 | 5,173,170美元 |
| 第三 | 3,727,023美元 |
| 第四 | 2,791,983 美元 |
| 第五 | 2,106,526美元 |
| 第六 | 1,600,792美元 |
| 第七 | 1,225,224美元 |
| 第八 | 944,593美元 |
| 第九 | 733,224美元 |
假设每位玩家的水平相同,获胜概率可以用筹码占总筹码量的份额来估算。然而,之后的每个位置都会变得更加复杂。为了解答这个问题,我开发了扑克锦标赛计算器。
输入以上信息后,您会发现阿米尔的预期奖金为 3,658,046 美元。然后减去第 9 名的最低奖金 733,224 美元,您将获得 2,924,822 美元的预期非保证奖金。每 1% 的份额价值 29,248.22 美元。这恰好是 cardplayer.com 文章中引用的价格。
顺便说一句,Lehavot 获得了第三名,奖金为 3,727,023 美元。扣除第九名的 733,224 美元保证金,再除以 100,每 1% 的份额可获得 29,938 美元的回报。每股原始成本为 29,248 美元,因此每股收益为 2.36%。
我在Wizard of Vegas论坛上讨论过这个问题。
对于那些仍然使用普通彩票(而非电子彩票)的赌场促销活动,玩家需要在玩家柜台打印彩票,然后将其放入转鼓中——在将彩票放入转鼓之前,你们会弯曲/折叠彩票吗?你认为弯曲的彩票被抽中的几率更大吗?
希望你满意。为了回答这个问题,我在Office Depot买了一大卷彩票。然后我把其中500张彩票放进一个纸袋里,一半对折,大约90度角,另一半展开。之后,我让六位志愿者每人每次抽取40到60张彩票,并进行替换,同时我记录结果。结果如下。
抽奖券实验
| 主题 | 折叠 | 展开 | 全部的 |
|---|---|---|---|
| 1 | 二十五 | 二十五 | 50 |
| 2 | 三十八 | 22 | 60 |
| 3 | 二十五 | 15 | 40 |
| 4 | 三十四 | 16 | 50 |
| 5 | 二十七 | 23 | 50 |
| 6 | 二十六 | 24 | 50 |
| 全部的 | 175 | 125 | 300 |
因此,抽出的彩票中有 58.3% 被折叠了!
如果假设弃牌没有影响,那么这些结果将与预期相差2.89个标准差。假设弃牌不影响中奖概率,那么获得这么多或更多弃牌彩票的概率为0.19%,即514分之一。
我想补充的是,那些匆忙抽奖的受试者更有可能抽到弃牌。而那些每次抽奖都小心谨慎的受试者,抽到弃牌的概率接近或接近一半一半。
所以,我的结论肯定是放弃它们。
有关此问题的讨论,请访问我在Wizard of Vegas 的论坛。
两位玩家分别获得一个 (0,1) 中的随机数。第一位玩家决定是维持现状还是弃牌并抽取新的数字。第二位玩家也同样决定。数字大的玩家获胜。每位玩家的最佳策略是什么?假设采用最佳策略,每位玩家获胜的概率是多少?
假设你有机会玩抛硬币游戏。如果第一次抛出正面,你将获得 2 美元,游戏结束。否则,你需要再次抛硬币。如果第二次抛出正面,你将获得 4 美元。如果第二次还是反面,你就继续抛硬币,直到抛出正面。每次抛硬币,奖金都会翻倍。换句话说,你将获得 2^n 美元的奖金,其中 n 是抛硬币的次数(包括最后一次抛出正面)。你愿意花多少钱来玩这个游戏?我听说数学答案是无限的钱,但这说不通,因为你最终赢得的钱是有限的。
这就是所谓的圣彼得堡悖论。
确实,游戏的预期赢利是∞,但同时硬币最终出现反面的概率是存在的,最终赢的钱是有限的。预期赢利的计算方法如下:
预期赢利 = pr(1 次翻转)×2 + pr(2 次翻转)×4 + pr(3 次翻转)×8 + pr(4 次翻转)×16 + pr(5 次翻转)×32 + pr(6 次翻转)×64 + ... =
(1/2) 1 × 2 1 + (1/2) 2 × 2 2 + (1/2) 3 × 2 3 + (1/2) 4 × 2 4 + (1/2) 5 × 2 5 + (1/2) 6 × 2 6 + ...
= ((1/2)*(2/1)) 1 + ((1/2)*(2/1)) 2 + ((1/2)*(2/1)) 3 + ((1/2)*(2/1)) 4 + ((1/2)*(2/1)) 5 + ((1/2)*(2/1)) 6 + ...
= 1 1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + ...
= 1 + 1 + 1 + 1 + 1 + 1 + ... = ∞
矛盾的是,玩家必须赢得有限的金额,但预期赢取的金额却是无限的。这怎么可能呢?
这或许不是一个令人满意的答案,但关于无穷大,确实存在很多悖论。这或许会让我收到一些愤怒的邮件,但尽管存在这些无穷大悖论,让我晚上睡得安稳的是,我相信无穷大是一个数学或哲学概念,在现实物理宇宙中尚未得到证实。这个无穷大的概念或理论本身就带有悖论。
对于那些不同意这一点的人,请告诉我任何被证明具有无限数量或测量的东西。除非你有黑洞大小的证据,否则请不要说黑洞的密度是无限的。
要回答最初关于玩这个游戏应该花多少钱的问题,我们应该记住,幸福感并不与金钱的数量成正比。我个人在经济学课上学习过,我相信金钱带来的效用,或者说幸福感,与金钱数量的对数成正比。在这个假设下,如果将任何两个人的财富增加或减少相同的百分比(初始财富不为零),那么他们都会体验到相同的幸福感变化。例如,如果吉姆的财富突然从 1,000 美元增加到 1,100 美元,而约翰的财富突然从 10,000,000 美元增加到 1,1,000,000 美元,那么他们都会体验到相同的幸福感增长,因为在这两种情况下,他们的财富都增加了 10%。假设金钱带来的幸福感确实与金额的对数成正比,那么下表显示了一个人在付费玩游戏之前,根据其财富应该愿意支付的最高金额。
玩的冷漠程度
| 财富 | 漠不关心 数量 |
|---|---|
| 10美元 | 4.97 美元 |
| 100美元 | 7.79美元 |
| 1,000 美元 | 10.96美元 |
| 10,000 美元 | 14.26美元 |
| 10万美元 | 17.78 美元 |
| 100万美元 | 20.88 美元 |
| 1000万美元 | 24.19美元 |
| 1亿美元 | 27.51美元 |
| 10亿美元 | 30.84美元 |
由此可见,在现实情况下,您应该支付的金额远低于∞美元。例如,如果您的财富是一百万美元,那么您应该对花费20.88美元进行游戏无所谓。
这个问题是在我的“拉斯维加斯巫师”论坛上提出并讨论的。
密歇根州彩票有一款三人游戏,规则如下: 在这场游戏中,最后出局有什么位置优势吗?每位玩家的最佳策略是什么? 这里有一个YouTube视频,展示了这场游戏。
首先,最后行动没有任何位置优势。由于在前面的玩家进行游戏时,玩家会被安排在隔音室内,所以顺序并不重要。
其次,博弈中必须存在一个纳什均衡,其中至少获得 x 分的策略优于其他任何策略。问题在于找到 x。
我问自己,如果每位玩家拿到的不是1到100的牌,而是0到1之间均匀分布的随机数,并寻找一个点x,让完美的逻辑学家对停牌和换牌无感,那么策略会是什么。有了这个答案,我们就能很容易地将答案应用到1到100的离散分布中。
我就不多说了,让读者自己体会这个问题的乐趣吧。查看下面的链接获取答案和解决方案。
答案为从 0 到 1 的连续分布。
答案为 1 到 100 的离散分布。
如需了解我的解决方案,请点击此处(PDF) 。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
假设你有一副牌,有十张红牌和十张黑牌。随机洗牌后,你不重复地抽牌。先抽出十张黑牌,再抽出五张红牌的概率是多少?
这就像问14张随机牌中全部包含10张黑牌的概率是多少。从一副牌中的10张红牌中,有(10,4)=210种方法可以选出4张红牌。当然,只有一种方法可以选出全部10张黑牌。从20张牌中,有(20,14)=38,760种方法可以选出14张。所以答案是210/38,760=0.005418,即1/184.57。
我知道有个促销活动,13个等级的牌全部拿到四张同点牌就能获得奖金。平均需要多少手牌才能达到这个水平?
让我们看看视频扑克的黄金标准,9-6 Jacks or Better来回答您的问题。
第一步是修改我的计算器,使其包含所有13种四类赔付的明细项目。修改后的收益表如下:
修改后的 Jacks 或 Better 回报表
| 事件 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 皇家同花顺 | 800 | 493,512,264 | 0.000025 | 0.019807 |
| 同花顺 | 50 | 2,178,883,296 | 0.000109 | 0.005465 |
| 四A | 二十五 | 3,900,253,596 | 0.000196 | 0.004892 |
| 四K | 二十五 | 3,904,533,816 | 0.000196 | 0.004897 |
| 四问 | 二十五 | 3,898,370,196 | 0.000196 | 0.004889 |
| 四J | 二十五 | 3,886,872,684 | 0.000195 | 0.004875 |
| 四个10 | 二十五 | 3,471,687,732 | 0.000174 | 0.004354 |
| 四个9 | 二十五 | 3,503,226,684 | 0.000176 | 0.004394 |
| 四个8 | 二十五 | 3,504,128,652 | 0.000176 | 0.004395 |
| 四个7 | 二十五 | 3,504,825,252 | 0.000176 | 0.004396 |
| 四6 | 二十五 | 3,504,861,888 | 0.000176 | 0.004396 |
| 四五 | 二十五 | 3,504,895,944 | 0.000176 | 0.004396 |
| 四4 | 二十五 | 3,504,032,676 | 0.000176 | 0.004395 |
| 四3 | 二十五 | 3,503,177,148 | 0.000176 | 0.004394 |
| 四2 | 二十五 | 3,502,301,496 | 0.000176 | 0.004393 |
| 客满 | 9 | 229,475,482,596 | 0.011512 | 0.103610 |
| 冲洗 | 6 | 219,554,786,160 | 0.011015 | 0.066087 |
| 直的 | 4 | 223,837,565,784 | 0.011229 | 0.044917 |
| 三条 | 3 | 1,484,003,070,324 | 0.074449 | 0.223346 |
| 两对 | 2 | 2,576,946,164,148 | 0.129279 | 0.258558 |
| 杰克或更好 | 1 | 4,277,372,890,968 | 0.214585 | 0.214585 |
| 没有什么 | 0 | 10,872,274,993,896 | 0.545435 | 0.000000 |
| 全部的 | 19,933,230,517,200 | 1.000000 | 0.995439 |
获得任意四张同点牌的概率为 0.002363。
下一个需要回答的问题是,平均需要多少次四张牌才能凑齐全部13种组合?为了回答这个问题,我创建了预期试验次数计算器。使用时,请在前13个单元格中输入每种四张牌的组合次数。计算器会告诉你,平均需要41.532646次四张牌才能凑齐全部13种组合。
因此,获得全部 13 张四条所需的预期手数为 41.341739/0.002363 = 17,580。
一片草地可以精确地喂养:
一头牛和一只骆驼,21天。
一只骆驼和一只绵羊,42天。
一羊一牛,28天。
牛吃的草和骆驼和绵羊加起来一样多。
草以恒定的速度生长。
这三只动物一起要花多长时间才能完全吃掉这片草地?
[/spoiler] 让:
c = 牛吃草的速率
l = 骆驼吃草的比率
s = 羊吃草的速率
g = 草的生长率
在一段时间结束时,消耗的草量必须等于初始草量加上该时间段内生长的草量。所以……
(1)21*(c+l)=1+21g
(2)42*(l+s)=1+42g
(3)28*(s+c)=1+28g
其中 1 代表一片草地。
我们还得到:
(4)c=s+l
首先,将公式(4)代入公式(2):
(5)42c = 1 + 42g
用 g 来表示:
(6)g = (42c-1)/42
接下来,将方程(6)代入(1)...
(7)21(c+l)=1+21*(42c-1)/42
经过一些代数运算,我们得到...
(8)l = 1/42。
接下来,将方程 (4) 代入 (3)...
(9)28*(2秒+1)=1+28克
我们知道 l=1/42,所以...
28*(2秒+1/42)=1+28克
56秒+28/42=1+28克
2352秒+28=42+1176克
(10)g = (2352秒 - 14)/1176
接下来,将方程(8)和(10)代入(2)中……
42*(1/42 + 秒) = 1 + 42*(2352秒 - 14)/1176
经过一些简单的代数运算,我们得到:
(11)s = 14/1176 = 1/84
根据公式(4)
(12)c =(1/84)+(1/42)=3/84=1/28
因此,如果草不长,那么牛需要 28 天才能吃完田地,骆驼需要 42 天,羊需要 84 天。
接下来,我们来求解 g。将 (11) 代入 (10) 中:
g = [2352*(1/84)-14]/1176
(13)g = 14/1176 = 1/84。
巧合的是,这与羊吃草的速度相同。
设t为最终答案。我们知道,在t天内,吃掉的草的数量必然等于田地里的草量(1)加上当时生长的草量。所以……
(13)t*(s+l+c)=1+tg
解决...
t*[(1/84) + (1/42) + (1/28)] = 1 + t/84
t = 1/[(1/84) + (1/42) + (1/28) - (1/84)]
(14)t = 84/5 = 16.8 天 = 16 天 19 小时 12 分钟
[/spoiler]
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
单位正方形内两个随机点之间的平均距离是多少?
对于一个如此简单的问题,解答起来却相当复杂。按照我的方法,你需要知道这个积分。
这是答案和我的解决方案(PDF) 。
这其实相当简单,尤其对于麻省理工学院的组合数学课程来说。题目描述如下:
“画出所有大小为 n=10 的同胚不可约树。”
以下是我尝试用简单易懂的英语表达的。
仅使用直线,画出所有交点和死角之和等于10的图形。不能有任何闭环。也不能有两个等值的图形。任何交点都必须至少有三条路径从该交点延伸出去。
你可能会问,“等效”是什么意思?意思是你可以随意移动棋子,但交叉点保持不变,而且不会产生任何新的棋子。
以下是一个例子: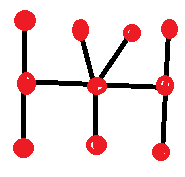
我给你个提示。和电影里的答案不一样,答案有十个。威尔只答对了八个。看看你能不能追上甚至超过威尔·亨特。
[/spoiler]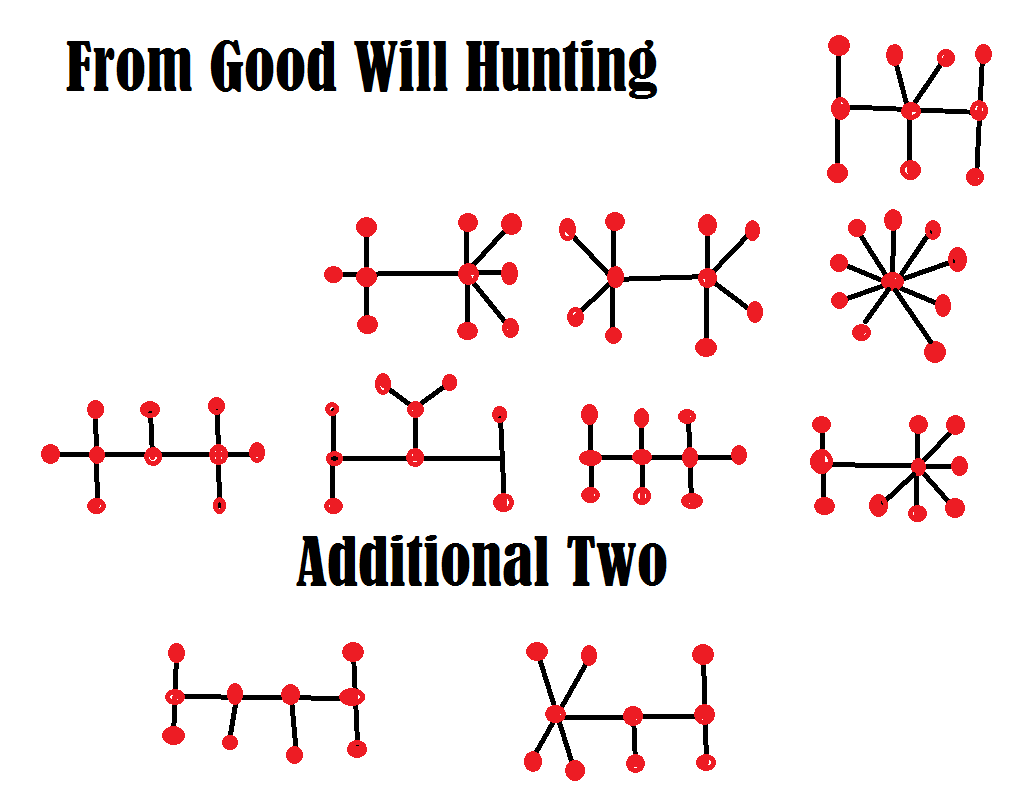
我在我的MathProblems.info网站问题 220 上展示了得出全部十个问题的逻辑。
[/剧透] 进一步阅读:- 《心灵捕手 II》中的数学:从学生的角度看问题——关于该问题的学术论文。
- 心灵捕手数学问题——在我的论坛中讨论这个问题。
考虑一个具有以下规则的游戏:
- 随机数生成器提供 0 到 1 之间均匀分布的随机数。
- 两名玩家各自获得一个号码。每位玩家只能看到自己的号码。
- 玩家 1 可以保留他的初始数字或换成一个新的随机数字。
- 玩家 2 知道玩家 1 的动作,可以选择保留原来的号码或换成新的号码。
- 数字较大的玩家获胜。
我对这个游戏有四个问题:
- 回答有关游戏的以下问题:
- 当数字为多少时,玩家 1 不会对站立和切换产生兴趣?
- 假设玩家 1 切换,那么玩家 2 在什么数字时应该无视站立和切换?
- 假设玩家 1 站立,那么玩家 2 在什么数字时应该无视站立和切换?
- 假设两位玩家都采用最佳策略,那么玩家 1 获胜的概率是多少?
答案和解决方案可以在我的数学问题页面第 225 题中找到。
我正在参加2018年的“死亡池”活动。规则如下:
- 每位参赛者必须提交一份十位 100 岁以下在世名人的名单。
- 如果任何名人在 2018 年去世(美联社提到有证据证明),那么名单上有该名人名字的任何人都将获得 100-x 分,其中 x 是去世时的年龄。
- 2019 年 1 月 1 日得分最高的玩家获胜。
从平均值来看,这个游戏的最佳策略是什么?
作为一名前精算师,你问对人了。希望精算师协会不会认为我的回答是对职业的滥用。话虽如此,为了回答你的问题,我查阅了我之前工作单位——社会保障局首席精算师办公室——的2014年期间寿命表。
周期生命表显示了 2014 年任何特定年龄和性别的人的死亡概率等。利用这些信息,我创建了下表,其中显示了从 0 到 100 岁的所有年龄段和两种性别的死亡概率和预期分数。
2014年期间生命表死亡池
| 年龄 | 概率 死亡——男性 | 概率 死亡——女性 | 预期的 积分 — 男性 | 预期的 积分 — 女性 |
|---|---|---|---|---|
| 0 | 0.006320 | 0.005310 | 0.632000 | 0.531000 |
| 1 | 0.000403 | 0.000352 | 0.039852 | 0.034835 |
| 2 | 0.000282 | 0.000221 | 0.027626 | 0.021683 |
| 3 | 0.000211 | 0.000161 | 0.020514 | 0.015612 |
| 4 | 0.000181 | 0.000131 | 0.017405 | 0.012556 |
| 5 | 0.000161 | 0.000111 | 0.015313 | 0.010515 |
| 6 | 0.000141 | 0.000111 | 0.013260 | 0.010405 |
| 7 | 0.000131 | 0.000101 | 0.012184 | 0.009360 |
| 8 | 0.000121 | 0.000091 | 0.011127 | 0.008334 |
| 9 | 0.000091 | 0.000081 | 0.008256 | 0.007328 |
| 10 | 0.000101 | 0.000091 | 0.009073 | 0.008154 |
| 11 | 0.000101 | 0.000081 | 0.008973 | 0.007168 |
| 12 | 0.000131 | 0.000101 | 0.011535 | 0.008861 |
| 十三 | 0.000202 | 0.000131 | 0.017547 | 0.011389 |
| 14 | 0.000303 | 0.000151 | 0.026023 | 0.012992 |
| 15 | 0.000404 | 0.000191 | 0.034304 | 0.016267 |
| 16 | 0.000505 | 0.000232 | 0.042393 | 0.019464 |
| 17 | 0.000616 | 0.000272 | 0.051129 | 0.022582 |
| 18 | 0.000748 | 0.000302 | 0.061316 | 0.024796 |
| 19 | 0.000880 | 0.000343 | 0.071262 | 0.027768 |
| 20 | 0.001022 | 0.000373 | 0.081780 | 0.029855 |
| 21 | 0.001145 | 0.000404 | 0.090445 | 0.031884 |
| 22 | 0.001258 | 0.000444 | 0.098105 | 0.034643 |
| 23 | 0.001310 | 0.000475 | 0.100880 | 0.036546 |
| 24 | 0.001332 | 0.000495 | 0.101246 | 0.037625 |
| 二十五 | 0.001344 | 0.000526 | 0.100811 | 0.039422 |
| 二十六 | 0.001377 | 0.000556 | 0.101864 | 0.041162 |
| 二十七 | 0.001389 | 0.000577 | 0.101371 | 0.042106 |
| 二十八 | 0.001421 | 0.000608 | 0.102330 | 0.043740 |
| 二十九 | 0.001454 | 0.000648 | 0.103234 | 0.046036 |
| 三十 | 0.001507 | 0.000669 | 0.105517 | 0.046837 |
| 31 | 0.001530 | 0.000710 | 0.105584 | 0.048998 |
| 三十二 | 0.001574 | 0.000751 | 0.107011 | 0.051084 |
| 33 | 0.001617 | 0.000813 | 0.108364 | 0.054454 |
| 三十四 | 0.001661 | 0.000864 | 0.109644 | 0.057041 |
| 三十五 | 0.001716 | 0.000926 | 0.111521 | 0.060194 |
| 三十六 | 0.001781 | 0.001008 | 0.113970 | 0.064538 |
| 三十七 | 0.001857 | 0.001081 | 0.116963 | 0.068090 |
| 三十八 | 0.001933 | 0.001164 | 0.119830 | 0.072145 |
| 三十九 | 0.002020 | 0.001237 | 0.123207 | 0.075427 |
| 40 | 0.002118 | 0.001340 | 0.127066 | 0.080422 |
| 41 | 0.002258 | 0.001445 | 0.133232 | 0.085232 |
| 四十二 | 0.002410 | 0.001560 | 0.139778 | 0.090455 |
| 43 | 0.002615 | 0.001696 | 0.149075 | 0.096649 |
| 四十四 | 0.002843 | 0.001853 | 0.159228 | 0.103761 |
| 45 | 0.003105 | 0.002011 | 0.170771 | 0.110606 |
| 46 | 0.003401 | 0.002191 | 0.183635 | 0.118300 |
| 四十七 | 0.003742 | 0.002403 | 0.198314 | 0.127342 |
| 四十八 | 0.004108 | 0.002647 | 0.213613 | 0.137656 |
| 49 | 0.004532 | 0.002894 | 0.231133 | 0.147577 |
| 50 | 0.004994 | 0.003194 | 0.249696 | 0.159718 |
| 51 | 0.005473 | 0.003487 | 0.268191 | 0.170880 |
| 52 | 0.005993 | 0.003794 | 0.287656 | 0.182103 |
| 53 | 0.006565 | 0.004104 | 0.308561 | 0.192871 |
| 54 | 0.007159 | 0.004428 | 0.329324 | 0.203676 |
| 55 | 0.007799 | 0.004767 | 0.350946 | 0.214498 |
| 56 | 0.008475 | 0.005153 | 0.372902 | 0.226729 |
| 57 | 0.009179 | 0.005534 | 0.394696 | 0.237972 |
| 58 | 0.009856 | 0.005889 | 0.413944 | 0.247347 |
| 59 | 0.010575 | 0.006272 | 0.433558 | 0.257150 |
| 60 | 0.011350 | 0.006683 | 0.453991 | 0.267338 |
| 61 | 0.012209 | 0.007180 | 0.476135 | 0.280016 |
| 62 | 0.013061 | 0.007720 | 0.496330 | 0.293355 |
| 63 | 0.013921 | 0.008339 | 0.515084 | 0.308537 |
| 64 | 0.014814 | 0.009029 | 0.533320 | 0.325041 |
| 65 | 0.015831 | 0.009839 | 0.554094 | 0.344371 |
| 66 | 0.016981 | 0.010741 | 0.577354 | 0.365197 |
| 67 | 0.018300 | 0.011752 | 0.603909 | 0.387812 |
| 68 | 0.019778 | 0.012879 | 0.632894 | 0.412117 |
| 69 | 0.021443 | 0.014142 | 0.664734 | 0.438397 |
| 70 | 0.023384 | 0.015613 | 0.701513 | 0.468376 |
| 71 | 0.025547 | 0.017271 | 0.740873 | 0.500852 |
| 72 | 0.027877 | 0.019047 | 0.780560 | 0.533320 |
| 73 | 0.030384 | 0.020918 | 0.820374 | 0.564797 |
| 74 | 0.033098 | 0.022938 | 0.860535 | 0.596385 |
| 75 | 0.036256 | 0.025299 | 0.906400 | 0.632465 |
| 76 | 0.039868 | 0.028043 | 0.956841 | 0.673035 |
| 77 | 0.043883 | 0.031127 | 1.009299 | 0.715914 |
| 78 | 0.048257 | 0.034590 | 1.061657 | 0.760984 |
| 79 | 0.053128 | 0.038456 | 1.115692 | 0.807583 |
| 80 | 0.058709 | 0.043007 | 1.174177 | 0.860145 |
| 81 | 0.065070 | 0.048186 | 1.236322 | 0.915536 |
| 82 | 0.072149 | 0.053762 | 1.298691 | 0.967712 |
| 83 | 0.079906 | 0.059769 | 1.358409 | 1.016065 |
| 84 | 0.088524 | 0.066380 | 1.416378 | 1.062085 |
| 85 | 0.098157 | 0.073823 | 1.472348 | 1.107351 |
| 86 | 0.108904 | 0.082381 | 1.524651 | 1.153334 |
| 87 | 0.120889 | 0.092180 | 1.571556 | 1.198344 |
| 88 | 0.134134 | 0.103305 | 1.609607 | 1.239664 |
| 89 | 0.148707 | 0.115744 | 1.635778 | 1.273180 |
| 90 | 0.164522 | 0.129477 | 1.645220 | 1.294772 |
| 91 | 0.181584 | 0.144435 | 1.634254 | 1.299911 |
| 92 | 0.199903 | 0.160621 | 1.599225 | 1.284970 |
| 93 | 0.219362 | 0.177816 | 1.535534 | 1.244713 |
| 94 | 0.239881 | 0.196194 | 1.439286 | 1.177165 |
| 95 | 0.260293 | 0.214694 | 1.301463 | 1.073469 |
| 96 | 0.280129 | 0.233056 | 1.120515 | 0.932225 |
| 97 | 0.299042 | 0.251152 | 0.897125 | 0.753456 |
| 98 | 0.316317 | 0.268235 | 0.632634 | 0.536471 |
| 99 | 0.332667 | 0.284442 | 0.332667 | 0.284442 |
| 100 | 0.348651 | 0.301417 | 0.000000 | 0.000000 |
该表显示,90 岁男性的最高预期分数为 1.645220。
这个问题是在我的非赌博论坛“Diversity Tomorrow”中提出和讨论的。
如果要将 355 毫升的液体装入罐中,那么罐子的尺寸应该是多少才能使表面积最小?
问得好!我之前在游戏展上看到一些细长的汽水罐,容量和标准尺寸的一样,都是355毫升,就好奇这个问题了。肯定不可能两个都对(别叫我雪莉)。[/spoiler] 让:
r = 罐体的半径
h = 罐子的高度
v = 罐子的体积
s=罐的表面积
我们从简单的几何知识中知道表面积 = 2*pi*r^2 + 2*pi*r*h。
同样,我们也知道体积是 pi*r^2*h,等于 355。
所以,355=pi*r^2*h。
让我们重新排列一下:
(1)h = 355/(π*r^2)
我们知道:
(2)s = 2*pi*r^2 + 2*pi*r*h。
我们将方程 (1) 中 h 的表达式代入 (2) 中,将其变为只有一个变量的函数:
s = 2*pi*r^2 + + 2*pi*r*(355/(pi*r^2))) = 2*pi*r^2 + 710/r。
让我们取 s 的导数并将其设置为零,以求解最优 r。
ds/dr = 4*pi*r - 710/(r^2) = 0
4*pi*r = 710/(r^2)
将两边乘以 r^2:
4*pi*r^3 = 710
r^3 = 177.5/pi。
r = (177.5/pi)^(1/3) = 3.837215248。
将该值代入公式 (1) 可得 h = 7.674430496。[/spoiler]
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
在我看来,我认识的大多数博彩专业人士更喜欢用方差而不是标准差来表示游戏的波动性。当然,前者只是后者的平方。然而,我更喜欢标准差,因为它的单位与投注和赢/输相同。也许他们喜欢用更大的数字来突出更大的波动性?您怎么看?赌徒们是否更喜欢使用“方差”?如果是,为什么?
我同意你听到的关于游戏方差的讨论比标准差更多,我一直觉得这有点烦人。我认为赌徒应该关心游戏波动性的原因是,他们把输赢与一局游戏的概率联系起来。比如,玩200手二十一点后,1%的输钱率算什么?要回答这个问题,你可以用二十一点的标准差,大约是1.15,具体取决于规则。
这个问题的具体答案是 1.15 × 200^0.5 × -2.32635(即高斯曲线上的 1%)= 低于预期 -37.83 个单位。别忘了,由于赌场优势,你可能会损失一些钱。假设赌场优势为 0.3%,那么 200 手牌之后,你可能会损失 0.003*200 = 0.6 手牌。因此,1% 的损失将是 0.6 + 37.83 = 38.43 手牌。
我听说,在美国,离婚率通常为50%,这个数字是用同一时期内离婚数量与结婚数量之比来计算的。是这样吗?您认为这种统计方法公平吗?我对此表示怀疑,因为您研究的是短期内的离婚数量,而不是长期婚姻的数量。
如果人口和年龄分布稳定,那么如果离婚概率真的是 50%,那么在样本量较大的情况下,我们预计在任何给定的时间段内都会看到一起离婚与两起结婚的比例。
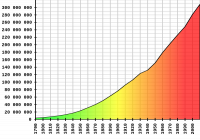
然而,人口并不稳定。从这张图表来看,美国人口每十年增长10.71%,相当于每年1.02%。为了简单起见,我们就假设是1%吧。
地图来源:美国人口普查
据fatherly.com称,失败的婚姻平均持续 8 年。
如果您观察到目前离婚与结婚的比例为 1 比 2,那么任何特定婚姻以离婚告终的平均概率是多少?
我们现在看到的离婚案例是8年前结婚的,当时的人口比例是现在的92.35%。简单的计算表明,真实的离婚概率是54.14%。
我们来检查一下。
首先,根据疾病预防控制中心的数据,每年每1000人中就有6.9对结婚。这个数字与本文的问题无关,但我认为有助于理解所涉及的数字。
假设8年前人口为3亿,那么当年结婚的人数为0.69%*3亿=207万对。
如果其中 54.14% 的人在八年后以离婚告终,那么我们现在将看到 2,070,000 * 54.14% = 1,120,698 起离婚事件。
1,120,698 / 2,070,000 = 目前观察到的离婚与结婚比率的 50%。
免得有人说,是的,我知道并非所有离婚都会在八年内结束。然而,综合考虑,我认为最终结果与我54.14%的真实离婚率相差无几。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
你的办公室有100名员工,他们会举行一个秘密圣诞礼物交换活动。你会把每个人的名字写在一张纸上,然后把纸放进一顶帽子里,然后每个人随机抽取一个名字作为礼物送给他们。
问题是,平均下来会有多少个闭环?比如说,戈登把钱给了唐,唐又给了乔恩,乔恩又给了内森,内森又给了戈登。或者抽自己的名字。
假设每个人每次选择一个。每个人选择时,会出现两种情况:
- 挑选者的名字已经被挑选了。
- 挑选者的名字仍然在名字箱里。
对于任何给定的挑选者,假设还有 n 个人需要挑选。
如果正在挑选名字的人的名字已经被选中,那么挑选者有 1/n 的概率会选择与他名字相关的名字,从而形成一个闭环。例如,假设艾米正在挑选。艾米的名字已经被鲍勃占据,鲍勃的名字已经被查理占据,而查理的名字仍然在箱子里。由于箱子里还有 n 个名字,所以艾米选择查理名字的概率为 1/n,从而形成一个闭环。
如果选择者的名字尚未被选中,那么艾米选择自己名字的概率为 1/n,从而形成一个循环。
无论如何,如果拾取者没有完成一个循环,她就加入了另一个链条的一部分,而这个链条最终会被其他人完成。每个链条在完成时只应被计算一次。
因此答案是 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518。
对于任何足够多的玩家数量 n 的估计值是 ln(n)。
这个问题是在我的Wizard of Vegas论坛中提出并讨论的。
为了纪念“询问巫师”专栏#314,您最喜欢的可以求和为某个 π 函数的无穷级数是什么?
选择这两个很容易,因为它们可能是最著名的两个:
- 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
- 1/1^2 + 1/2^2 + 1/3^2 + 1/4^2 + ... = π^2/6
我听说,随机抽取23个人,其中至少两人生日相同的概率超过50%?这是真的吗?其他规模的群体中,生日相同的概率是多少?对于3人、4人和5人,生日相同的概率也一样。
确实如此,随机选取23个人,至少有一对生日相同的概率是50.73%。这个概率忽略了闰日,并假设每个人在其他365天出生的概率相同(实际上并非如此,春季和秋季的生日概率略高一些)。
回答你问题的表格很长,所以我会把它们放在剧透标签里。点击按钮查看答案。
[剧透=两个人的共同生日]两人以上共同的生日
| 团体规模 | 可能性 |
|---|---|
| 2 | 0.002740 |
| 3 | 0.008204 |
| 4 | 0.016356 |
| 5 | 0.027136 |
| 6 | 0.040462 |
| 7 | 0.056236 |
| 8 | 0.074335 |
| 9 | 0.094624 |
| 10 | 0.116948 |
| 11 | 0.141141 |
| 12 | 0.167025 |
| 十三 | 0.194410 |
| 14 | 0.223103 |
| 15 | 0.252901 |
| 16 | 0.283604 |
| 17 | 0.315008 |
| 18 | 0.346911 |
| 19 | 0.379119 |
| 20 | 0.411438 |
| 21 | 0.443688 |
| 22 | 0.475695 |
| 23 | 0.507297 |
| 24 | 0.538344 |
| 二十五 | 0.568700 |
| 二十六 | 0.598241 |
| 二十七 | 0.626859 |
| 二十八 | 0.654461 |
| 二十九 | 0.680969 |
| 三十 | 0.706316 |
| 31 | 0.730455 |
| 三十二 | 0.753348 |
| 33 | 0.774972 |
| 三十四 | 0.795317 |
| 三十五 | 0.814383 |
| 三十六 | 0.832182 |
| 三十七 | 0.848734 |
| 三十八 | 0.864068 |
| 三十九 | 0.878220 |
| 40 | 0.891232 |
| 41 | 0.903152 |
| 四十二 | 0.914030 |
| 43 | 0.923923 |
| 四十四 | 0.932885 |
| 45 | 0.940976 |
| 46 | 0.948253 |
| 四十七 | 0.954774 |
| 四十八 | 0.960598 |
| 49 | 0.965780 |
| 50 | 0.970374 |
| 51 | 0.974432 |
| 52 | 0.978005 |
| 53 | 0.981138 |
| 54 | 0.983877 |
| 55 | 0.986262 |
| 56 | 0.988332 |
| 57 | 0.990122 |
| 58 | 0.991665 |
| 59 | 0.992989 |
| 60 | 0.994123 |
| 61 | 0.995089 |
| 62 | 0.995910 |
| 63 | 0.996604 |
| 64 | 0.997190 |
| 65 | 0.997683 |
| 66 | 0.998096 |
| 67 | 0.998440 |
| 68 | 0.998726 |
| 69 | 0.998964 |
| 70 | 0.999160 |
| 71 | 0.999321 |
| 72 | 0.999453 |
| 73 | 0.999561 |
| 74 | 0.999649 |
| 75 | 0.999720 |
| 76 | 0.999777 |
| 77 | 0.999824 |
| 78 | 0.999861 |
| 79 | 0.999891 |
| 80 | 0.999914 |
| 81 | 0.999933 |
| 82 | 0.999948 |
| 83 | 0.999960 |
| 84 | 0.999969 |
3 人以上共同的生日
| 团体规模 | 可能性 |
|---|---|
| 3 | 0.000008 |
| 4 | 0.000030 |
| 5 | 0.000075 |
| 6 | 0.000149 |
| 7 | 0.000261 |
| 8 | 0.000416 |
| 9 | 0.000623 |
| 10 | 0.000888 |
| 11 | 0.001218 |
| 12 | 0.001621 |
| 十三 | 0.002102 |
| 14 | 0.002670 |
| 15 | 0.003329 |
| 16 | 0.004088 |
| 17 | 0.004953 |
| 18 | 0.005929 |
| 19 | 0.007024 |
| 20 | 0.008243 |
| 21 | 0.009592 |
| 22 | 0.011078 |
| 23 | 0.012705 |
| 24 | 0.014481 |
| 二十五 | 0.016409 |
| 二十六 | 0.018497 |
| 二十七 | 0.020747 |
| 二十八 | 0.023167 |
| 二十九 | 0.025760 |
| 三十 | 0.028531 |
| 31 | 0.031484 |
| 三十二 | 0.034624 |
| 33 | 0.037954 |
| 三十四 | 0.041479 |
| 三十五 | 0.045202 |
| 三十六 | 0.049126 |
| 三十七 | 0.053254 |
| 三十八 | 0.057589 |
| 三十九 | 0.062133 |
| 40 | 0.066889 |
| 41 | 0.071859 |
| 四十二 | 0.077044 |
| 43 | 0.082446 |
| 四十四 | 0.088065 |
| 45 | 0.093903 |
| 46 | 0.099960 |
| 四十七 | 0.106236 |
| 四十八 | 0.112731 |
| 49 | 0.119444 |
| 50 | 0.126375 |
| 51 | 0.133522 |
| 52 | 0.140885 |
| 53 | 0.148460 |
| 54 | 0.156246 |
| 55 | 0.164241 |
| 56 | 0.172441 |
| 57 | 0.180844 |
| 58 | 0.189445 |
| 59 | 0.198242 |
| 60 | 0.207230 |
| 61 | 0.216405 |
| 62 | 0.225761 |
| 63 | 0.235294 |
| 64 | 0.244999 |
| 65 | 0.254869 |
| 66 | 0.264899 |
| 67 | 0.275082 |
| 68 | 0.285413 |
| 69 | 0.295883 |
| 70 | 0.306487 |
| 71 | 0.317217 |
| 72 | 0.328066 |
| 73 | 0.339026 |
| 74 | 0.350088 |
| 75 | 0.361246 |
| 76 | 0.372491 |
| 77 | 0.383814 |
| 78 | 0.395207 |
| 79 | 0.406662 |
| 80 | 0.418169 |
| 81 | 0.429720 |
| 82 | 0.441307 |
| 83 | 0.452920 |
| 84 | 0.464550 |
| 85 | 0.476188 |
| 86 | 0.487826 |
| 87 | 0.499455 |
| 88 | 0.511065 |
| 89 | 0.522648 |
| 90 | 0.534196 |
| 91 | 0.545698 |
| 92 | 0.557148 |
| 93 | 0.568537 |
| 94 | 0.579855 |
| 95 | 0.591096 |
| 96 | 0.602252 |
| 97 | 0.613314 |
| 98 | 0.624275 |
| 99 | 0.635127 |
| 100 | 0.645865 |
| 101 | 0.656480 |
| 102 | 0.666967 |
| 103 | 0.677318 |
| 104 | 0.687529 |
| 105 | 0.697593 |
| 106 | 0.707505 |
| 107 | 0.717260 |
| 108 | 0.726853 |
| 109 | 0.736279 |
| 110 | 0.745536 |
| 111 | 0.754619 |
| 112 | 0.763525 |
| 113 | 0.772251 |
| 114 | 0.780795 |
| 115 | 0.789155 |
| 116 | 0.797330 |
| 117 | 0.805319 |
| 118 | 0.813121 |
| 119 | 0.820580 |
| 120 | 0.827964 |
| 121 | 0.835152 |
| 122 | 0.842144 |
| 123 | 0.848940 |
| 124 | 0.855540 |
| 125 | 0.861945 |
| 126 | 0.868155 |
| 127 | 0.874172 |
| 128 | 0.879996 |
| 129 | 0.885631 |
| 130 | 0.891076 |
| 131 | 0.896335 |
| 132 | 0.901409 |
| 133 | 0.906302 |
| 134 | 0.911015 |
| 135 | 0.915552 |
| 136 | 0.919915 |
| 137 | 0.924108 |
| 138 | 0.928135 |
| 139 | 0.931997 |
| 140 | 0.935700 |
| 141 | 0.939246 |
| 142 | 0.942640 |
| 143 | 0.945885 |
| 144 | 0.948985 |
| 145 | 0.951944 |
| 146 | 0.954766 |
| 147 | 0.957456 |
| 148 | 0.960016 |
| 149 | 0.962452 |
| 150 | 0.964767 |
| 151 | 0.966965 |
| 152 | 0.969050 |
| 153 | 0.971028 |
| 154 | 0.972900 |
| 155 | 0.974672 |
| 156 | 0.976347 |
| 157 | 0.977930 |
| 158 | 0.979423 |
| 159 | 0.980831 |
| 160 | 0.982158 |
| 161 | 0.983407 |
| 162 | 0.984581 |
| 163 | 0.985684 |
| 164 | 0.986719 |
| 165 | 0.987690 |
| 166 | 0.988600 |
| 167 | 0.989452 |
| 168 | 0.990248 |
| 169 | 0.990992 |
| 170 | 0.991687 |
| 171 | 0.992335 |
| 172 | 0.992938 |
| 173 | 0.993500 |
| 174 | 0.994022 |
| 175 | 0.994508 |
| 176 | 0.994958 |
| 177 | 0.995376 |
| 178 | 0.995763 |
| 179 | 0.996121 |
| 180 | 0.996452 |
| 181 | 0.996758 |
| 182 | 0.997040 |
| 183 | 0.997300 |
| 184 | 0.997540 |
| 185 | 0.997760 |
| 186 | 0.997963 |
| 187 | 0.998149 |
| 188 | 0.998319 |
| 189 | 0.998476 |
| 190 | 0.998619 |
| 191 | 0.998750 |
| 192 | 0.998869 |
| 193 | 0.998979 |
| 194 | 0.999078 |
| 195 | 0.999169 |
| 196 | 0.999251 |
| 197 | 0.999326 |
| 198 | 0.999394 |
| 199 | 0.999456 |
| 200 | 0.999512 |
| 201 | 0.999562 |
| 202 | 0.999608 |
| 203 | 0.999650 |
| 204 | 0.999687 |
| 205 | 0.999720 |
| 206 | 0.999751 |
| 207 | 0.999778 |
| 208 | 0.999802 |
| 209 | 0.999824 |
| 210 | 0.999844 |
| 211 | 0.999862 |
| 212 | 0.999877 |
| 213 | 0.999891 |
| 214 | 0.999904 |
| 215 | 0.999915 |
| 216 | 0.999925 |
| 217 | 0.999934 |
| 218 | 0.999942 |
| 219 | 0.999949 |
| 220 | 0.999955 |
| 221 | 0.999961 |
| 222 | 0.999966 |
| 223 | 0.999970 |
| 224 | 0.999974 |
| 225 | 0.999977 |
| 226 | 0.999980 |
| 227 | 0.999982 |
| 228 | 0.999985 |
| 229 | 0.999987 |
| 230 | 0.999988 |
| 231 | 0.999990 |
| 232 | 0.999991 |
| 233 | 0.999992 |
| 234 | 0.999994 |
| 235 | 0.999994 |
| 236 | 0.999995 |
| 237 | 0.999996 |
| 238 | 0.999996 |
| 239 | 0.999997 |
| 240 | 0.999997 |
| 241 | 0.999998 |
| 242 | 0.999998 |
| 243 | 0.999998 |
| 244 | 0.999999 |
4 人以上共同的生日
| 团体规模 | 可能性 |
|---|---|
| 4 | 0.000000 |
| 5 | 0.000000 |
| 6 | 0.000000 |
| 7 | 0.000001 |
| 8 | 0.000001 |
| 9 | 0.000003 |
| 10 | 0.000004 |
| 11 | 0.000007 |
| 12 | 0.000010 |
| 十三 | 0.000014 |
| 14 | 0.000020 |
| 15 | 0.000027 |
| 16 | 0.000036 |
| 17 | 0.000048 |
| 18 | 0.000061 |
| 19 | 0.000077 |
| 20 | 0.000096 |
| 21 | 0.000119 |
| 22 | 0.000145 |
| 23 | 0.000175 |
| 24 | 0.000209 |
| 二十五 | 0.000248 |
| 二十六 | 0.000293 |
| 二十七 | 0.000343 |
| 二十八 | 0.000399 |
| 二十九 | 0.000462 |
| 三十 | 0.000532 |
| 31 | 0.000610 |
| 三十二 | 0.000695 |
| 33 | 0.000790 |
| 三十四 | 0.000893 |
| 三十五 | 0.001006 |
| 三十六 | 0.001129 |
| 三十七 | 0.001263 |
| 三十八 | 0.001408 |
| 三十九 | 0.001566 |
| 40 | 0.001736 |
| 41 | 0.001919 |
| 四十二 | 0.002116 |
| 43 | 0.002328 |
| 四十四 | 0.002555 |
| 45 | 0.002798 |
| 46 | 0.003058 |
| 四十七 | 0.003334 |
| 四十八 | 0.003629 |
| 49 | 0.003943 |
| 50 | 0.004276 |
| 51 | 0.004629 |
| 52 | 0.005003 |
| 53 | 0.005399 |
| 54 | 0.005817 |
| 55 | 0.006258 |
| 56 | 0.006724 |
| 57 | 0.007214 |
| 58 | 0.007730 |
| 59 | 0.008272 |
| 60 | 0.008841 |
| 61 | 0.009439 |
| 62 | 0.010065 |
| 63 | 0.010721 |
| 64 | 0.011408 |
| 65 | 0.012126 |
| 66 | 0.012876 |
| 67 | 0.013659 |
| 68 | 0.014476 |
| 69 | 0.015327 |
| 70 | 0.016215 |
| 71 | 0.017139 |
| 72 | 0.018100 |
| 73 | 0.019099 |
| 74 | 0.020137 |
| 75 | 0.021215 |
| 76 | 0.022334 |
| 77 | 0.023495 |
| 78 | 0.024698 |
| 79 | 0.025944 |
| 80 | 0.027235 |
| 81 | 0.028570 |
| 82 | 0.029951 |
| 83 | 0.031379 |
| 84 | 0.032855 |
| 85 | 0.034379 |
| 86 | 0.035952 |
| 87 | 0.037575 |
| 88 | 0.039249 |
| 89 | 0.040974 |
| 90 | 0.042752 |
| 91 | 0.044583 |
| 92 | 0.046467 |
| 93 | 0.048407 |
| 94 | 0.050402 |
| 95 | 0.052453 |
| 96 | 0.054561 |
| 97 | 0.056726 |
| 98 | 0.058950 |
| 99 | 0.061233 |
| 100 | 0.063576 |
| 101 | 0.065978 |
| 102 | 0.068442 |
| 103 | 0.070967 |
| 104 | 0.073554 |
| 105 | 0.076204 |
| 106 | 0.078917 |
| 107 | 0.081694 |
| 108 | 0.084535 |
| 109 | 0.087441 |
| 110 | 0.090412 |
| 111 | 0.093449 |
| 112 | 0.096552 |
| 113 | 0.099722 |
| 114 | 0.102958 |
| 115 | 0.106262 |
| 116 | 0.109633 |
| 117 | 0.113072 |
| 118 | 0.116579 |
| 119 | 0.120154 |
| 120 | 0.123798 |
| 121 | 0.127510 |
| 122 | 0.131292 |
| 123 | 0.135142 |
| 124 | 0.139061 |
| 125 | 0.143050 |
| 126 | 0.147107 |
| 127 | 0.151234 |
| 128 | 0.155429 |
| 129 | 0.159694 |
| 130 | 0.164027 |
| 131 | 0.168429 |
| 132 | 0.172899 |
| 133 | 0.177438 |
| 134 | 0.182044 |
| 135 | 0.186719 |
| 136 | 0.191460 |
| 137 | 0.196269 |
| 138 | 0.201144 |
| 139 | 0.206085 |
| 140 | 0.211091 |
| 141 | 0.216163 |
| 142 | 0.221299 |
| 143 | 0.226499 |
| 144 | 0.231763 |
| 145 | 0.237089 |
| 146 | 0.242476 |
| 147 | 0.247925 |
| 148 | 0.253434 |
| 149 | 0.259002 |
| 150 | 0.264629 |
| 151 | 0.270314 |
| 152 | 0.276055 |
| 153 | 0.281852 |
| 154 | 0.287703 |
| 155 | 0.293608 |
| 156 | 0.299566 |
| 157 | 0.305575 |
| 158 | 0.311634 |
| 159 | 0.317741 |
| 160 | 0.323897 |
| 161 | 0.330099 |
| 162 | 0.336346 |
| 163 | 0.342637 |
| 164 | 0.348970 |
| 165 | 0.355343 |
| 166 | 0.361757 |
| 167 | 0.368208 |
| 168 | 0.374696 |
| 169 | 0.381218 |
| 170 | 0.387774 |
| 171 | 0.394362 |
| 172 | 0.400980 |
| 173 | 0.407626 |
| 174 | 0.414299 |
| 175 | 0.420997 |
| 176 | 0.427718 |
| 177 | 0.434462 |
| 178 | 0.441224 |
| 179 | 0.448005 |
| 180 | 0.454803 |
| 181 | 0.461615 |
| 182 | 0.468439 |
| 183 | 0.475274 |
| 184 | 0.482118 |
| 185 | 0.488969 |
| 186 | 0.495826 |
| 187 | 0.502685 |
| 188 | 0.509546 |
| 189 | 0.516407 |
| 190 | 0.523265 |
| 191 | 0.530119 |
| 192 | 0.536967 |
| 193 | 0.543807 |
| 194 | 0.550636 |
| 195 | 0.557454 |
| 196 | 0.564258 |
| 197 | 0.571046 |
| 198 | 0.577817 |
| 199 | 0.584568 |
| 200 | 0.591298 |
| 201 | 0.598005 |
| 202 | 0.604687 |
| 203 | 0.611342 |
| 204 | 0.617969 |
| 205 | 0.624565 |
| 206 | 0.631129 |
| 207 | 0.637659 |
| 208 | 0.644154 |
| 209 | 0.650611 |
| 210 | 0.657030 |
| 211 | 0.663407 |
| 212 | 0.669743 |
| 213 | 0.676035 |
| 214 | 0.682281 |
| 215 | 0.688481 |
| 216 | 0.694632 |
| 217 | 0.700734 |
| 218 | 0.706784 |
| 219 | 0.712782 |
| 220 | 0.718726 |
| 221 | 0.724614 |
| 222 | 0.730446 |
| 223 | 0.736220 |
| 224 | 0.741936 |
| 225 | 0.747591 |
| 226 | 0.753185 |
| 227 | 0.758717 |
| 228 | 0.764185 |
| 229 | 0.769590 |
| 230 | 0.774929 |
| 231 | 0.780202 |
| 232 | 0.785409 |
| 233 | 0.790547 |
| 234 | 0.795618 |
| 235 | 0.800619 |
| 236 | 0.805551 |
| 237 | 0.810412 |
| 238 | 0.815202 |
| 239 | 0.819921 |
| 240 | 0.824569 |
| 241 | 0.829144 |
| 242 | 0.833646 |
| 243 | 0.838076 |
| 244 | 0.842432 |
| 245 | 0.846716 |
| 246 | 0.850925 |
| 247 | 0.855061 |
| 248 | 0.859123 |
| 249 | 0.863112 |
| 250 | 0.867027 |
| 251 | 0.870868 |
| 252 | 0.874635 |
| 253 | 0.878329 |
| 254 | 0.881950 |
| 255 | 0.885498 |
| 256 | 0.888973 |
| 257 | 0.892375 |
| 258 | 0.895705 |
| 259 | 0.898964 |
| 260 | 0.902151 |
| 261 | 0.905268 |
| 262 | 0.908314 |
| 263 | 0.911290 |
| 264 | 0.914197 |
| 265 | 0.917036 |
| 266 | 0.919806 |
| 267 | 0.922509 |
| 268 | 0.925145 |
| 269 | 0.927715 |
| 270 | 0.930220 |
| 271 | 0.932661 |
| 272 | 0.935037 |
| 273 | 0.937351 |
| 274 | 0.939603 |
| 275 | 0.941793 |
| 276 | 0.943923 |
| 277 | 0.945993 |
| 278 | 0.948005 |
| 279 | 0.949960 |
| 280 | 0.951857 |
| 281 | 0.953699 |
| 282 | 0.955486 |
| 283 | 0.957218 |
| 284 | 0.958898 |
| 285 | 0.960527 |
| 286 | 0.962104 |
| 287 | 0.963631 |
| 288 | 0.965109 |
| 289 | 0.966540 |
| 290 | 0.967923 |
| 291 | 0.969260 |
| 292 | 0.970553 |
| 293 | 0.971802 |
| 294 | 0.973007 |
| 295 | 0.974171 |
| 296 | 0.975294 |
| 297 | 0.976377 |
| 298 | 0.977421 |
| 299 | 0.978427 |
| 300 | 0.979397 |
| 301 | 0.980330 |
| 302 | 0.981228 |
| 303 | 0.982092 |
| 304 | 0.982923 |
| 305 | 0.983722 |
| 306 | 0.984490 |
| 307 | 0.985227 |
| 308 | 0.985935 |
| 309 | 0.986614 |
| 310 | 0.987266 |
| 311 | 0.987890 |
| 312 | 0.988489 |
| 313 | 0.989063 |
| 314 | 0.989612 |
| 315 | 0.990138 |
| 316 | 0.990641 |
| 317 | 0.991122 |
| 318 | 0.991581 |
| 319 | 0.992021 |
| 320 | 0.992440 |
| 321 | 0.992841 |
| 322 | 0.993223 |
| 323 | 0.993587 |
| 324 | 0.993935 |
| 325 | 0.994266 |
| 326 | 0.994581 |
| 327 | 0.994882 |
| 328 | 0.995167 |
| 329 | 0.995439 |
| 330 | 0.995698 |
| 331 | 0.995943 |
| 332 | 0.996176 |
| 333 | 0.996398 |
| 334 | 0.996608 |
| 335 | 0.996807 |
| 336 | 0.996996 |
| 337 | 0.997175 |
| 338 | 0.997344 |
| 339 | 0.997505 |
| 340 | 0.997657 |
| 341 | 0.997801 |
| 342 | 0.997936 |
| 343 | 0.998065 |
| 344 | 0.998186 |
| 345 | 0.998300 |
| 346 | 0.998408 |
| 347 | 0.998510 |
| 348 | 0.998606 |
| 349 | 0.998696 |
| 350 | 0.998781 |
| 351 | 0.998861 |
| 352 | 0.998937 |
| 353 | 0.999008 |
| 354 | 0.999074 |
| 355 | 0.999137 |
| 356 | 0.999195 |
| 357 | 0.999250 |
| 358 | 0.999302 |
| 359 | 0.999350 |
| 360 | 0.999396 |
| 361 | 0.999438 |
| 362 | 0.999478 |
| 363 | 0.999515 |
| 364 | 0.999550 |
| 365 | 0.999582 |
| 366 | 0.999613 |
| 367 | 0.999641 |
| 368 | 0.999668 |
| 369 | 0.999692 |
| 370 | 0.999715 |
| 371 | 0.999736 |
| 372 | 0.999756 |
| 373 | 0.999775 |
| 374 | 0.999792 |
| 375 | 0.999808 |
| 376 | 0.999823 |
| 377 | 0.999837 |
| 378 | 0.999850 |
| 379 | 0.999861 |
| 380 | 0.999872 |
| 381 | 0.999883 |
| 382 | 0.999892 |
| 383 | 0.999901 |
| 384 | 0.999909 |
| 385 | 0.999916 |
| 386 | 0.999923 |
| 387 | 0.999930 |
| 388 | 0.999935 |
| 389 | 0.999941 |
| 390 | 0.999946 |
| 391 | 0.999950 |
| 392 | 0.999955 |
| 393 | 0.999959 |
| 394 | 0.999962 |
| 395 | 0.999965 |
| 396 | 0.999969 |
| 397 | 0.999971 |
| 398 | 0.999974 |
| 399 | 0.999976 |
| 400 | 0.999978 |
| 401 | 0.999980 |
| 402 | 0.999982 |
| 403 | 0.999984 |
| 404 | 0.999985 |
| 405 | 0.999987 |
| 406 | 0.999988 |
| 407 | 0.999989 |
| 408 | 0.999990 |
| 409 | 0.999991 |
| 410 | 0.999992 |
| 411 | 0.999993 |
| 412 | 0.999993 |
| 413 | 0.999994 |
| 414 | 0.999995 |
| 415 | 0.999995 |
| 416 | 0.999996 |
| 417 | 0.999996 |
| 418 | 0.999996 |
| 419 | 0.999997 |
| 420 | 0.999997 |
| 421 | 0.999997 |
| 422 | 0.999998 |
| 423 | 0.999998 |
| 424 | 0.999998 |
| 425 | 0.999998 |
| 426 | 0.999998 |
| 427 | 0.999999 |
| 428 | 0.999999 |
| 429 | 0.999999 |
5 人以上共同的生日
| 团体规模 | 可能性 |
|---|---|
| 5 | 0.000000 |
| 6 | 0.000000 |
| 7 | 0.000000 |
| 8 | 0.000000 |
| 9 | 0.000000 |
| 10 | 0.000000 |
| 11 | 0.000000 |
| 12 | 0.000000 |
| 十三 | 0.000000 |
| 14 | 0.000000 |
| 15 | 0.000000 |
| 16 | 0.000000 |
| 17 | 0.000000 |
| 18 | 0.000001 |
| 19 | 0.000001 |
| 20 | 0.000001 |
| 21 | 0.000001 |
| 22 | 0.000002 |
| 23 | 0.000002 |
| 24 | 0.000003 |
| 二十五 | 0.000004 |
| 二十六 | 0.000004 |
| 二十七 | 0.000005 |
| 二十八 | 0.000006 |
| 二十九 | 0.000008 |
| 三十 | 0.000009 |
| 31 | 0.000011 |
| 三十二 | 0.000013 |
| 33 | 0.000015 |
| 三十四 | 0.000017 |
| 三十五 | 0.000020 |
| 三十六 | 0.000023 |
| 三十七 | 0.000026 |
| 三十八 | 0.000030 |
| 三十九 | 0.000034 |
| 40 | 0.000039 |
| 41 | 0.000044 |
| 四十二 | 0.000050 |
| 43 | 0.000056 |
| 四十四 | 0.000063 |
| 45 | 0.000070 |
| 46 | 0.000079 |
| 四十七 | 0.000087 |
| 四十八 | 0.000097 |
| 49 | 0.000108 |
| 50 | 0.000119 |
| 51 | 0.000132 |
| 52 | 0.000145 |
| 53 | 0.000159 |
| 54 | 0.000175 |
| 55 | 0.000192 |
| 56 | 0.000209 |
| 57 | 0.000229 |
| 58 | 0.000249 |
| 59 | 0.000271 |
| 60 | 0.000295 |
| 61 | 0.000320 |
| 62 | 0.000347 |
| 63 | 0.000375 |
| 64 | 0.000406 |
| 65 | 0.000438 |
| 66 | 0.000472 |
| 67 | 0.000509 |
| 68 | 0.000547 |
| 69 | 0.000588 |
| 70 | 0.000631 |
| 71 | 0.000676 |
| 72 | 0.000725 |
| 73 | 0.000775 |
| 74 | 0.000829 |
| 75 | 0.000885 |
| 76 | 0.000944 |
| 77 | 0.001007 |
| 78 | 0.001072 |
| 79 | 0.001141 |
| 80 | 0.001213 |
| 81 | 0.001289 |
| 82 | 0.001369 |
| 83 | 0.001452 |
| 84 | 0.001539 |
| 85 | 0.001630 |
| 86 | 0.001726 |
| 87 | 0.001825 |
| 88 | 0.001930 |
| 89 | 0.002038 |
| 90 | 0.002152 |
| 91 | 0.002270 |
| 92 | 0.002394 |
| 93 | 0.002522 |
| 94 | 0.002656 |
| 95 | 0.002796 |
| 96 | 0.002941 |
| 97 | 0.003092 |
| 98 | 0.003249 |
| 99 | 0.003412 |
| 100 | 0.003581 |
| 101 | 0.003757 |
| 102 | 0.003939 |
| 103 | 0.004128 |
| 104 | 0.004325 |
| 105 | 0.004528 |
| 106 | 0.004739 |
| 107 | 0.004957 |
| 108 | 0.005183 |
| 109 | 0.005417 |
| 110 | 0.005659 |
| 111 | 0.005909 |
| 112 | 0.006168 |
| 113 | 0.006436 |
| 114 | 0.006712 |
| 115 | 0.006998 |
| 116 | 0.007293 |
| 117 | 0.007597 |
| 118 | 0.007912 |
| 119 | 0.008236 |
| 120 | 0.008570 |
| 121 | 0.008915 |
| 122 | 0.009270 |
| 123 | 0.009636 |
| 124 | 0.010013 |
| 125 | 0.010402 |
| 126 | 0.010801 |
| 127 | 0.011213 |
| 128 | 0.011637 |
| 129 | 0.012072 |
| 130 | 0.012521 |
| 131 | 0.012981 |
| 132 | 0.013455 |
| 133 | 0.013942 |
| 134 | 0.014442 |
| 135 | 0.014956 |
| 136 | 0.015484 |
| 137 | 0.016026 |
| 138 | 0.016582 |
| 139 | 0.017153 |
| 140 | 0.017739 |
| 141 | 0.018340 |
| 142 | 0.018956 |
| 143 | 0.019588 |
| 144 | 0.020235 |
| 145 | 0.020899 |
| 146 | 0.021580 |
| 147 | 0.022277 |
| 148 | 0.022991 |
| 149 | 0.023722 |
| 150 | 0.024470 |
| 151 | 0.025237 |
| 152 | 0.026021 |
| 153 | 0.026824 |
| 154 | 0.027645 |
| 155 | 0.028485 |
| 156 | 0.029344 |
| 157 | 0.030222 |
| 158 | 0.031120 |
| 159 | 0.032037 |
| 160 | 0.032975 |
| 161 | 0.033934 |
| 162 | 0.034913 |
| 163 | 0.035912 |
| 164 | 0.036934 |
| 165 | 0.037976 |
| 166 | 0.039040 |
| 167 | 0.040127 |
| 168 | 0.041235 |
| 169 | 0.042367 |
| 170 | 0.043521 |
| 171 | 0.044698 |
| 172 | 0.045898 |
| 173 | 0.047122 |
| 174 | 0.048370 |
| 175 | 0.049642 |
| 176 | 0.050939 |
| 177 | 0.052260 |
| 178 | 0.053606 |
| 179 | 0.054977 |
| 180 | 0.056374 |
| 181 | 0.057796 |
| 182 | 0.059245 |
| 183 | 0.060719 |
| 184 | 0.062220 |
| 185 | 0.063748 |
| 186 | 0.065302 |
| 187 | 0.066884 |
| 188 | 0.068493 |
| 189 | 0.070130 |
| 190 | 0.071795 |
| 191 | 0.073487 |
| 192 | 0.075209 |
| 193 | 0.076958 |
| 194 | 0.078737 |
| 195 | 0.080544 |
| 196 | 0.082381 |
| 197 | 0.084247 |
| 198 | 0.086143 |
| 199 | 0.088068 |
| 200 | 0.090024 |
| 201 | 0.092009 |
| 202 | 0.094026 |
| 203 | 0.096072 |
| 204 | 0.098150 |
| 205 | 0.100259 |
| 206 | 0.102398 |
| 207 | 0.104569 |
| 208 | 0.106772 |
| 209 | 0.109006 |
| 210 | 0.111272 |
| 211 | 0.113570 |
| 212 | 0.115899 |
| 213 | 0.118262 |
| 214 | 0.120656 |
| 215 | 0.123083 |
| 216 | 0.125542 |
| 217 | 0.128035 |
| 218 | 0.130559 |
| 219 | 0.133117 |
| 220 | 0.135708 |
| 221 | 0.138332 |
| 222 | 0.140989 |
| 223 | 0.143679 |
| 224 | 0.146403 |
| 225 | 0.149160 |
| 226 | 0.151950 |
| 227 | 0.154774 |
| 228 | 0.157632 |
| 229 | 0.160522 |
| 230 | 0.163447 |
| 231 | 0.166405 |
| 232 | 0.169396 |
| 233 | 0.172421 |
| 234 | 0.175480 |
| 235 | 0.178572 |
| 236 | 0.181698 |
| 237 | 0.184857 |
| 238 | 0.188049 |
| 239 | 0.191275 |
| 240 | 0.194534 |
| 241 | 0.197827 |
| 242 | 0.201152 |
| 243 | 0.204511 |
| 244 | 0.207902 |
| 245 | 0.211327 |
| 246 | 0.214784 |
| 247 | 0.218274 |
| 248 | 0.221796 |
| 249 | 0.225351 |
| 250 | 0.228937 |
| 251 | 0.232556 |
| 252 | 0.236207 |
| 253 | 0.239889 |
| 254 | 0.243603 |
| 255 | 0.247348 |
| 256 | 0.251124 |
| 257 | 0.254931 |
| 258 | 0.258768 |
| 259 | 0.262636 |
| 260 | 0.266534 |
| 261 | 0.270462 |
| 262 | 0.274419 |
| 263 | 0.278406 |
| 264 | 0.282422 |
| 265 | 0.286466 |
| 266 | 0.290539 |
| 267 | 0.294639 |
| 268 | 0.298768 |
| 269 | 0.302924 |
| 270 | 0.307106 |
| 271 | 0.311316 |
| 272 | 0.315551 |
| 273 | 0.319813 |
| 274 | 0.324100 |
| 275 | 0.328412 |
| 276 | 0.332749 |
| 277 | 0.337110 |
| 278 | 0.341495 |
| 279 | 0.345903 |
| 280 | 0.350334 |
| 281 | 0.354788 |
| 282 | 0.359264 |
| 283 | 0.363761 |
| 284 | 0.368279 |
| 285 | 0.372818 |
| 286 | 0.377376 |
| 287 | 0.381955 |
| 288 | 0.386552 |
| 289 | 0.391167 |
| 290 | 0.395801 |
| 291 | 0.400452 |
| 292 | 0.405119 |
| 293 | 0.409803 |
| 294 | 0.414503 |
| 295 | 0.419217 |
| 296 | 0.423946 |
| 297 | 0.428689 |
| 298 | 0.433445 |
| 299 | 0.438214 |
| 300 | 0.442995 |
| 301 | 0.447787 |
| 302 | 0.452590 |
| 303 | 0.457403 |
| 304 | 0.462226 |
| 305 | 0.467057 |
| 306 | 0.471897 |
| 307 | 0.476744 |
| 308 | 0.481599 |
| 309 | 0.486459 |
| 310 | 0.491325 |
| 311 | 0.496196 |
| 312 | 0.501070 |
| 313 | 0.505949 |
| 314 | 0.510830 |
| 315 | 0.515713 |
| 316 | 0.520598 |
| 317 | 0.525483 |
| 318 | 0.530369 |
| 319 | 0.535253 |
| 320 | 0.540137 |
| 321 | 0.545018 |
| 322 | 0.549896 |
| 323 | 0.554771 |
| 324 | 0.559642 |
| 325 | 0.564507 |
| 326 | 0.569367 |
| 327 | 0.574221 |
| 328 | 0.579067 |
| 329 | 0.583906 |
| 330 | 0.588736 |
| 331 | 0.593557 |
| 332 | 0.598368 |
| 333 | 0.603169 |
| 334 | 0.607958 |
| 335 | 0.612735 |
| 336 | 0.617500 |
| 337 | 0.622251 |
| 338 | 0.626988 |
| 339 | 0.631710 |
| 340 | 0.636417 |
| 341 | 0.641107 |
| 342 | 0.645781 |
| 343 | 0.650437 |
| 344 | 0.655075 |
| 345 | 0.659695 |
| 346 | 0.664295 |
| 347 | 0.668875 |
| 348 | 0.673434 |
| 349 | 0.677972 |
| 350 | 0.682488 |
| 351 | 0.686981 |
| 352 | 0.691451 |
| 353 | 0.695897 |
| 354 | 0.700319 |
| 355 | 0.704716 |
| 356 | 0.709088 |
| 357 | 0.713433 |
| 358 | 0.717752 |
| 359 | 0.722043 |
| 360 | 0.726307 |
| 361 | 0.730543 |
| 362 | 0.734750 |
| 363 | 0.738927 |
| 364 | 0.743075 |
| 365 | 0.747193 |
| 366 | 0.751279 |
| 367 | 0.755335 |
| 368 | 0.759359 |
| 369 | 0.763351 |
| 370 | 0.767310 |
| 371 | 0.771237 |
| 372 | 0.775130 |
| 373 | 0.778990 |
| 374 | 0.782815 |
| 375 | 0.786606 |
| 376 | 0.790363 |
| 377 | 0.794084 |
| 378 | 0.797770 |
| 379 | 0.801420 |
| 380 | 0.805034 |
| 381 | 0.808611 |
| 382 | 0.812152 |
| 383 | 0.815656 |
| 384 | 0.819123 |
| 385 | 0.822553 |
| 386 | 0.825945 |
| 387 | 0.829300 |
| 388 | 0.832616 |
| 389 | 0.835895 |
| 390 | 0.839135 |
| 391 | 0.842336 |
| 392 | 0.845499 |
| 393 | 0.848624 |
| 394 | 0.851709 |
| 395 | 0.854756 |
| 396 | 0.857764 |
| 397 | 0.860733 |
| 398 | 0.863663 |
| 399 | 0.866553 |
| 400 | 0.869405 |
| 401 | 0.872217 |
| 402 | 0.874990 |
| 403 | 0.877724 |
| 404 | 0.880419 |
| 405 | 0.883075 |
| 406 | 0.885692 |
| 407 | 0.888269 |
| 408 | 0.890808 |
| 409 | 0.893309 |
| 410 | 0.895770 |
| 411 | 0.898193 |
| 412 | 0.900578 |
| 413 | 0.902924 |
| 414 | 0.905232 |
| 415 | 0.907502 |
| 416 | 0.909734 |
| 417 | 0.911929 |
| 418 | 0.914086 |
| 419 | 0.916205 |
| 420 | 0.918288 |
| 421 | 0.920334 |
| 422 | 0.922344 |
| 423 | 0.924317 |
| 424 | 0.926254 |
| 425 | 0.928155 |
| 426 | 0.930020 |
| 427 | 0.931851 |
| 428 | 0.933646 |
| 429 | 0.935406 |
| 430 | 0.937133 |
| 431 | 0.938825 |
| 432 | 0.940483 |
| 433 | 0.942108 |
| 434 | 0.943699 |
| 435 | 0.945258 |
| 436 | 0.946785 |
| 437 | 0.948279 |
| 438 | 0.949741 |
| 439 | 0.951173 |
| 440 | 0.952573 |
| 441 | 0.953942 |
| 442 | 0.955281 |
| 443 | 0.956590 |
| 444 | 0.957870 |
| 445 | 0.959120 |
| 446 | 0.960342 |
| 447 | 0.961535 |
| 448 | 0.962701 |
| 449 | 0.963838 |
| 450 | 0.964949 |
| 451 | 0.966032 |
| 452 | 0.967090 |
| 453 | 0.968121 |
| 454 | 0.969127 |
| 455 | 0.970107 |
| 456 | 0.971063 |
| 457 | 0.971994 |
| 458 | 0.972902 |
| 459 | 0.973785 |
| 460 | 0.974646 |
| 461 | 0.975484 |
| 462 | 0.976299 |
| 463 | 0.977093 |
| 464 | 0.977865 |
| 465 | 0.978616 |
| 466 | 0.979346 |
| 467 | 0.980056 |
| 468 | 0.980746 |
| 469 | 0.981416 |
| 470 | 0.982067 |
| 471 | 0.982699 |
| 472 | 0.983313 |
| 473 | 0.983909 |
| 474 | 0.984488 |
| 475 | 0.985049 |
| 476 | 0.985593 |
| 477 | 0.986121 |
| 478 | 0.986633 |
| 479 | 0.987128 |
| 480 | 0.987609 |
| 481 | 0.988074 |
| 482 | 0.988525 |
| 483 | 0.988962 |
| 484 | 0.989384 |
| 485 | 0.989793 |
| 486 | 0.990189 |
| 487 | 0.990571 |
| 488 | 0.990941 |
| 489 | 0.991299 |
| 490 | 0.991644 |
| 491 | 0.991978 |
| 492 | 0.992301 |
| 493 | 0.992612 |
| 494 | 0.992913 |
| 495 | 0.993203 |
| 496 | 0.993483 |
| 497 | 0.993753 |
| 498 | 0.994013 |
| 499 | 0.994264 |
| 500 | 0.994506 |
| 501 | 0.994740 |
| 502 | 0.994964 |
| 503 | 0.995180 |
| 504 | 0.995389 |
| 505 | 0.995589 |
| 506 | 0.995782 |
| 507 | 0.995967 |
| 508 | 0.996146 |
| 509 | 0.996317 |
| 510 | 0.996482 |
| 511 | 0.996640 |
| 512 | 0.996793 |
| 513 | 0.996939 |
| 514 | 0.997079 |
| 515 | 0.997213 |
| 516 | 0.997343 |
| 517 | 0.997466 |
| 518 | 0.997585 |
| 519 | 0.997699 |
| 520 | 0.997808 |
| 521 | 0.997913 |
| 522 | 0.998013 |
| 523 | 0.998109 |
| 524 | 0.998200 |
| 525 | 0.998288 |
| 526 | 0.998372 |
| 527 | 0.998452 |
| 528 | 0.998529 |
| 529 | 0.998602 |
| 530 | 0.998673 |
| 531 | 0.998739 |
| 532 | 0.998803 |
| 533 | 0.998864 |
| 534 | 0.998923 |
| 535 | 0.998978 |
| 536 | 0.999031 |
| 537 | 0.999082 |
| 538 | 0.999130 |
| 539 | 0.999176 |
| 540 | 0.999219 |
| 541 | 0.999261 |
| 542 | 0.999301 |
| 543 | 0.999338 |
| 544 | 0.999374 |
| 545 | 0.999408 |
| 546 | 0.999441 |
| 547 | 0.999471 |
| 548 | 0.999501 |
| 549 | 0.999528 |
| 550 | 0.999555 |
| 551 | 0.999580 |
| 552 | 0.999604 |
| 553 | 0.999626 |
| 554 | 0.999648 |
| 555 | 0.999668 |
| 556 | 0.999687 |
| 557 | 0.999705 |
| 558 | 0.999722 |
| 559 | 0.999739 |
| 560 | 0.999754 |
| 561 | 0.999769 |
| 562 | 0.999782 |
| 563 | 0.999795 |
| 564 | 0.999808 |
| 565 | 0.999819 |
| 566 | 0.999830 |
| 567 | 0.999841 |
| 568 | 0.999851 |
| 569 | 0.999860 |
| 570 | 0.999868 |
| 571 | 0.999877 |
| 572 | 0.999884 |
| 573 | 0.999892 |
| 574 | 0.999899 |
| 575 | 0.999905 |
| 576 | 0.999911 |
| 577 | 0.999917 |
| 578 | 0.999922 |
| 579 | 0.999927 |
| 580 | 0.999932 |
| 581 | 0.999936 |
| 582 | 0.999941 |
| 583 | 0.999945 |
| 584 | 0.999948 |
| 585 | 0.999952 |
| 586 | 0.999955 |
| 587 | 0.999958 |
| 588 | 0.999961 |
| 589 | 0.999964 |
| 590 | 0.999966 |
| 591 | 0.999968 |
| 592 | 0.999971 |
| 593 | 0.999973 |
| 594 | 0.999975 |
| 595 | 0.999976 |
| 596 | 0.999978 |
| 597 | 0.999980 |
| 598 | 0.999981 |
| 599 | 0.999982 |
| 600 | 0.999984 |
| 601 | 0.999985 |
| 602 | 0.999986 |
| 603 | 0.999987 |
| 604 | 0.999988 |
| 605 | 0.999989 |
| 606 | 0.999990 |
| 607 | 0.999990 |
| 608 | 0.999991 |
| 609 | 0.999992 |
| 610 | 0.999992 |
| 611 | 0.999993 |
| 612 | 0.999994 |
| 613 | 0.999994 |
| 614 | 0.999994 |
| 615 | 0.999995 |
| 616 | 0.999995 |
| 617 | 0.999996 |
| 618 | 0.999996 |
| 619 | 0.999996 |
| 620 | 0.999997 |
| 621 | 0.999997 |
| 622 | 0.999997 |
| 623 | 0.999997 |
| 624 | 0.999998 |
| 625 | 0.999998 |
| 626 | 0.999998 |
| 627 | 0.999998 |
| 628 | 0.999998 |
| 629 | 0.999998 |
| 630 | 0.999999 |
| 631 | 0.999999 |
| 632 | 0.999999 |
| 633 | 0.999999 |
| 634 | 0.999999 |
假设荷官手中有各种面额的筹码,这些筹码都能被1美元整除。你在赌桌上买入10美元。荷官会用多少种不同的方式找零这10美元?其他买入金额又如何呢?
庄家有 42 种方法可以把 10 美元分成 10 美元。具体如下:
[剧透=10 的分区] 109,1
8,2
8,1,1
7,3
7,2,1
7,1,1,1
6,4
6,3,1
6,2,2
6,2,1,1
6,1,1,1,1
5,5
5,4,1
5,3,2
5,3,1,1
5,2,2,1
5,2,1,1,1
5,1,1,1,1,1
4,4,2
4,4,1,1
4,3,3
4,3,2,1
4,3,1,1,1
4,2,2,2
4,2,2,1,1
4,2,1,1,1,1
4,1,1,1,1,1,1
3,3,3,1
3,3,2,2
3,3,2,1,1
3,3,1,1,1,1
3,2,2,2,1
3,2,2,1,1,1
3,2,1,1,1,1,1
3,1,1,1,1,1,1,1
2,2,2,2,2
2,2,2,2,1,1
2,2,2,1,1,1,1
2,2,1,1,1,1,1,1
2,1,1,1,1,1,1,1,1
1,1,1,1,1,1,1,1,1,1,1
数学家们把这些称为“分区”。以下是起始数量最多为 405 的分区数,这是我的计算机所能计算的最大数量(2^64)。
两人以上共同的生日
<!--/框标题-->| 最初的 数量 | 全部的 分区 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| 5 | 7 |
| 6 | 11 |
| 7 | 15 |
| 8 | 22 |
| 9 | 三十 |
| 10 | 四十二 |
| 11 | 56 |
| 12 | 77 |
| 十三 | 101 |
| 14 | 135 |
| 15 | 176 |
| 16 | 231 |
| 17 | 297 |
| 18 | 385 |
| 19 | 490 |
| 20 | 627 |
| 21 | 792 |
| 22 | 1002 |
| 23 | 1255 |
| 24 | 1575 |
| 二十五 | 1958 |
| 二十六 | 2436 |
| 二十七 | 3010 |
| 二十八 | 3718 |
| 二十九 | 4565 |
| 三十 | 5604 |
| 31 | 6842 |
| 三十二 | 8349 |
| 33 | 10143 |
| 三十四 | 12310 |
| 三十五 | 14883 |
| 三十六 | 17977 |
| 三十七 | 21637 |
| 三十八 | 26015 |
| 三十九 | 31185 |
| 40 | 37338 |
| 41 | 44583 |
| 四十二 | 53174 |
| 43 | 63261 |
| 四十四 | 75175 |
| 45 | 89134 |
| 46 | 105558 |
| 四十七 | 124754 |
| 四十八 | 147273 |
| 49 | 173525 |
| 50 | 204226 |
| 51 | 239943 |
| 52 | 281589 |
| 53 | 329931 |
| 54 | 386155 |
| 55 | 451276 |
| 56 | 526823 |
| 57 | 614154 |
| 58 | 715220 |
| 59 | 831820 |
| 60 | 966467 |
| 61 | 1121505 |
| 62 | 1300156 |
| 63 | 1505499 |
| 64 | 1741630 |
| 65 | 2012558 |
| 66 | 2323520 |
| 67 | 2679689 |
| 68 | 3087735 |
| 69 | 3554345 |
| 70 | 4087968 |
| 71 | 4697205 |
| 72 | 5392783 |
| 73 | 6185689 |
| 74 | 7089500 |
| 75 | 8118264 |
| 76 | 9289091 |
| 77 | 10619863 |
| 78 | 12132164 |
| 79 | 13848650 |
| 80 | 15796476 |
| 81 | 18004327 |
| 82 | 20506255 |
| 83 | 23338469 |
| 84 | 26543660 |
| 85 | 30167357 |
| 86 | 34262962 |
| 87 | 38887673 |
| 88 | 44108109 |
| 89 | 49995925 |
| 90 | 56634173 |
| 91 | 64112359 |
| 92 | 72533807 |
| 93 | 82010177 |
| 94 | 92669720 |
| 95 | 104651419 |
| 96 | 118114304 |
| 97 | 133230930 |
| 98 | 150198136 |
| 99 | 169229875 |
| 100 | 190569292 |
| 101 | 214481126 |
| 102 | 241265379 |
| 103 | 271248950 |
| 104 | 304801365 |
| 105 | 342325709 |
| 106 | 384276336 |
| 107 | 431149389 |
| 108 | 483502844 |
| 109 | 541946240 |
| 110 | 607163746 |
| 111 | 679903203 |
| 112 | 761002156 |
| 113 | 851376628 |
| 114 | 952050665 |
| 115 | 1064144451 |
| 116 | 1188908248 |
| 117 | 1327710076 |
| 118 | 1482074143 |
| 119 | 1653668665 |
| 120 | 1844349560 |
| 121 | 2056148051 |
| 122 | 2291320912 |
| 123 | 2552338241 |
| 124 | 2841940500 |
| 125 | 3163127352 |
| 126 | 3519222692 |
| 127 | 3913864295 |
| 128 | 4351078600 |
| 129 | 4835271870 |
| 130 | 5371315400 |
| 131 | 5964539504 |
| 132 | 6620830889 |
| 133 | 7346629512 |
| 134 | 8149040695 |
| 135 | 9035836076 |
| 136 | 10015581680 |
| 137 | 11097645016 |
| 138 | 12292341831 |
| 139 | 13610949895 |
| 140 | 15065878135 |
| 141 | 16670689208 |
| 142 | 18440293320 |
| 143 | 20390982757 |
| 144 | 22540654445 |
| 145 | 24908858009 |
| 146 | 27517052599 |
| 147 | 30388671978 |
| 148 | 33549419497 |
| 149 | 37027355200 |
| 150 | 40853235313 |
| 151 | 45060624582 |
| 152 | 49686288421 |
| 153 | 54770336324 |
| 154 | 60356673280 |
| 155 | 66493182097 |
| 156 | 73232243759 |
| 157 | 80630964769 |
| 158 | 88751778802 |
| 159 | 97662728555 |
| 160 | 107438159466 |
| 161 | 118159068427 |
| 162 | 129913904637 |
| 163 | 142798995930 |
| 164 | 156919475295 |
| 165 | 172389800255 |
| 166 | 189334822579 |
| 167 | 207890420102 |
| 168 | 228204732751 |
| 169 | 250438925115 |
| 170 | 274768617130 |
| 171 | 301384802048 |
| 172 | 330495499613 |
| 173 | 362326859895 |
| 174 | 397125074750 |
| 175 | 435157697830 |
| 176 | 476715857290 |
| 177 | 522115831195 |
| 178 | 571701605655 |
| 179 | 625846753120 |
| 180 | 684957390936 |
| 181 | 749474411781 |
| 182 | 819876908323 |
| 183 | 896684817527 |
| 184 | 980462880430 |
| 185 | 1071823774337 |
| 186 | 1171432692373 |
| 187 | 1280011042268 |
| 188 | 1398341745571 |
| 189 | 1527273599625 |
| 190 | 1667727404093 |
| 191 | 1820701100652 |
| 192 | 1987276856363 |
| 193 | 2168627105469 |
| 194 | 2366022741845 |
| 195 | 2580840212973 |
| 196 | 2814570987591 |
| 197 | 3068829878530 |
| 198 | 3345365983698 |
| 199 | 3646072432125 |
| 200 | 3972999029388 |
| 201 | 4328363658647 |
| 202 | 4714566886083 |
| 203 | 5134205287973 |
| 204 | 5590088317495 |
| 205 | 6085253859260 |
| 206 | 6622987708040 |
| 207 | 7206841706490 |
| 208 | 7840656226137 |
| 209 | 8528581302375 |
| 210 | 9275102575355 |
| 211 | 10085065885767 |
| 212 | 10963707205259 |
| 213 | 11916681236278 |
| 214 | 12950095925895 |
| 215 | 14070545699287 |
| 216 | 15285151248481 |
| 217 | 16601598107914 |
| 218 | 18028182516671 |
| 219 | 19573856161145 |
| 220 | 21248279009367 |
| 221 | 23061871173849 |
| 222 | 25025873760111 |
| 223 | 27152408925615 |
| 224 | 29454549941750 |
| 225 | 31946390696157 |
| 226 | 34643126322519 |
| 227 | 37561133582570 |
| 228 | 40718063627362 |
| 229 | 44132934884255 |
| 230 | 47826239745920 |
| 231 | 51820051838712 |
| 232 | 56138148670947 |
| 233 | 60806135438329 |
| 234 | 65851585970275 |
| 235 | 71304185514919 |
| 236 | 77195892663512 |
| 237 | 83561103925871 |
| 238 | 90436839668817 |
| 239 | 97862933703585 |
| 240 | 105882246722733 |
| 114540884553038 | |
| 242 | 123888443077259 |
| 243 | 133978259344888 |
| 244 | 144867692496445 |
| 245 | 156618412527946 |
| 246 | 169296722391554 |
| 247 | 182973889854026 |
| 248 | 197726516681672 |
| 249 | 213636919820625 |
| 250 | 230793554364681 |
| 251 | 249291451168559 |
| 252 | 269232701252579 |
| 253 | 290726957916112 |
| 254 | 313891991306665 |
| 255 | 338854264248680 |
| 256 | 365749566870782 |
| 257 | 394723676655357 |
| 258 | 425933084409356 |
| 259 | 459545750448675 |
| 260 | 495741934760846 |
| 261 | 534715062908609 |
| 262 | 576672674947168 |
| 263 | 621837416509615 |
| 264 | 670448123060170 |
| 265 | 722760953690372 |
| 266 | 779050629562167 |
| 267 | 839611730366814 |
| 268 | 904760108316360 |
| 269 | 974834369944625 |
| 270 | 1050197489931117 |
| 271 | 1131238503938606 |
| 272 | 1218374349844333 |
| 273 | 1312051800816215 |
| 274 | 1412749565173450 |
| 275 | 1520980492851175 |
| 276 | 1637293969337171 |
| 277 | 1762278433057269 |
| 278 | 1896564103591584 |
| 279 | 2040825852575075 |
| 280 | 2195786311682516 |
| 281 | 2362219145337711 |
| 282 | 2540952590045698 |
| 283 | 2732873183547535 |
| 284 | 2938929793929555 |
| 285 | 3160137867148997 |
| 286 | 3397584011986773 |
| 287 | 3652430836071053 |
| 288 | 3925922161489422 |
| 289 | 4219388528587095 |
| 290 | 4534253126900886 |
| 291 | 4872038056472084 |
| 292 | 5234371069753672 |
| 293 | 5622992691950605 |
| 294 | 6039763882095515 |
| 295 | 6486674127079088 |
| 296 | 6965850144195831 |
| 297 | 7479565078510584 |
| 298 | 8030248384943040 |
| 299 | 8620496275465025 |
| 300 | 9253082936723602 |
| 301 | 9930972392403501 |
| 302 | 10657331232548839 |
| 303 | 11435542077822104 |
| 304 | 12269218019229465 |
| 305 | 13162217895057704 |
| 306 | 14118662665280005 |
| 307 | 15142952738857194 |
| 308 | 16239786535829663 |
| 309 | 17414180133147295 |
| 310 | 18671488299600364 |
| 311 | 20017426762576945 |
| 312 | 21458096037352891 |
| 313 | 23000006655487337 |
| 314 | 24650106150830490 |
| 315 | 26415807633566326 |
| 316 | 28305020340996003 |
| 317 | 30326181989842964 |
| 318 | 32488293351466654 |
| 319 | 34800954869440830 |
| 320 | 37274405776748077 |
| 321 | 39919565526999991 |
| 322 | 42748078035954696 |
| 323 | 45772358543578028 |
| 324 | 49005643635237875 |
| 325 | 52462044228828641 |
| 326 | 56156602112874289 |
| 327 | 60105349839666544 |
| 328 | 64325374609114550 |
| 329 | 68834885946073850 |
| 330 | 73653287861850339 |
| 331 | 78801255302666615 |
| 332 | 84300815636225119 |
| 333 | 90175434980549623 |
| 334 | 96450110192202760 |
| 335 | 103151466321735325 |
| 336 | 110307860425292772 |
| 337 | 117949491546113972 |
| 338 | 126108517833796355 |
| 339 | 134819180623301520 |
| 340 | 144117936527873832 |
| 341 | 154043597379576030 |
| 342 | 164637479165761044d> |
| 343 | 175943559810422753 |
| 344 | 188008647052292980 |
| 345 | 200882556287683159 |
| 346 | 214618299743286299 |
| 347 | 229272286871217150 |
| 348 | 244904537455382406 |
| 349 | 261578907351144125 |
| 350 | 279363328483702152 |
| 351 | 298330063062758076 |
| 352 | 318555973788329084 |
| 353 | 340122810048577428 |
| 354 | 363117512048110005 |
| 355 | 387632532919029223 |
| 356 | 413766180933342362 |
| 357 | 441622981929358437 |
| 358 | 471314064268398780 |
| 359 | 502957566506000020 |
| 360 | 536679070310691121 |
| 361 | 572612058898037559 |
| 362 | 610898403751884101 |
| 363 | 651688879997206959 |
| 364 | 695143713458946040 |
| 365 | 741433159884081684 |
| 366 | 790738119649411319 |
| 367 | 843250788562528427 |
| 368 | 899175348396088349 |
| 369 | 958728697912338045 |
| 370 | 1022141228367345362 |
| 371 | 1089657644424399782 |
| 372 | 1161537834849962850 |
| 373 | 1238057794119125085 |
| 374 | 1319510599727473500 |
| 375 | 1406207446561484054 |
| 376 | 1498478743590581081 |
| 377 | 1596675274490756791 |
| 378 | 1701169427975813525 |
| 379 | 1812356499739472950 |
| 380 | 1930656072350465812 |
| 381 | 2056513475336633805 |
| 382 | 2190401332423765131 |
| 383 | 2332821198543892336 |
| 384 | 2484305294265418180 |
| 385 | 2645418340688763701 |
| 386 | 2816759503217942792 |
| 387 | 2998964447736452194 |
| 388 | 3192707518433532826 |
| 389 | 3398704041358160275 |
| 390 | 3617712763867604423 |
| 391 | 3850538434667429186 |
| 392 | 4098034535626594791 |
| 393 | 4361106170762284114 |
| 394 | 4640713124699623515 |
| 395 | 4937873096788191655 |
| 396 | 5253665124416975163 |
| 397 | 5589233202595404488 |
| 398 | 5945790114707874597 |
| 399 | 6324621482504294325 |
| 400 | 6727090051741041926 |
| 401 | 7154640222653942321 |
| 402 | 7608802843339879269 |
| 403 | 8091200276484465581 |
| 404 | 8603551759348655060 |
| 405 | 9147679068859117602 |
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
正如电影《贱女孩》中所问,什么是:
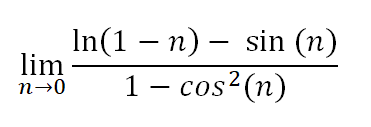
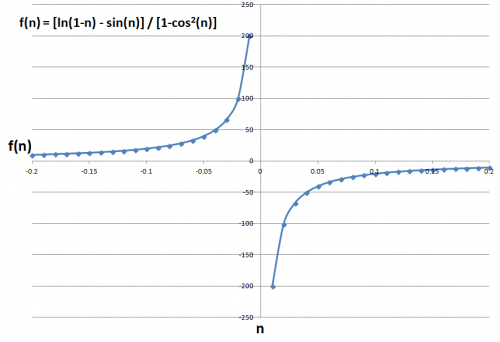
让我们首先查看 n(x 轴)乘以 f(n)(y 轴)的图表。
如你所见,极限从左边趋向于∞,从右边趋向于-∞。由于极限从两边不指向同一个位置,所以不存在极限。
不过,我们先不画图来回答这个问题。洛必达规则指出,如果 f(x)/g(x) 的极限 = 0/0,则 lim f(x)/g(x) = lim f'(x)/g'(x)。所以,我们来解 f'(x) 和 g'(x)。
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos 2 (n)) d/dn = sin 2 (n) d/dn
让我们用乘积法则来求解 sin 2 (n) d/dn
sin 2 (n) d/dn = sin(n) × sin(n) d/dn =
sin(n) × cos(n) + cos(n) × sin(n) =
2sin(n)cos(n)。
接下来,让我们求解 n = 0 时的 f'(n) 和 g'(n)。
f'(0)= -1/(1-0)-cos(0)= -2。
g'(0) = 2sin(0)cos(0) = 0
所以,f'(0)/g'(0) = -2/0 = -∞。因此,原函数的极限不存在。

我要夸赞《贱女孩》的编剧,他们把数学运用得炉火纯青。即使是像《心灵捕手》这样严肃的数学电影,也常常把数学运用得一塌糊涂。
在《少年谢尔顿》第三季第四集《霍比特人、物理学和拉链球》中,谢尔顿问自己一张宾果卡上可能的组合数。答案是什么?节目中显示的公式正确吗?
首先,我来介绍一下排列数。这意味着不仅数字重要,它们在卡片上的顺序也很重要。对于 B、I、G 和 O 列,可能的排列数为 permut(15,5) = 15!/(15-5)! = 15*14*13*12*11 = 360,360。对于 N 列,排列数为 permut(14,4) = 15!/(15-4)! = 15*14*13*12 = 32,760。因此,宾果卡的排列总数为 360,360 (4 × 32,760) = 552446474061128648601600000。
其次,我来讨论一下组合数。这意味着数字很重要,但它们在卡片上的顺序并不重要。对于 B、I、G 和 O 列,可能的组合数共有 combin(15,5) = 15!/(5!*(15-5)!) = (15*14*13*12*11)/(1*2*3*4*5) = 3,003 种。对于 N 列,排列数为 combin(14,4) = 15!/(4!*(15-4)!) = (15*14*13*12)/(1*2*3*4) = 1,365。因此,宾果卡的排列总数为 3,003 4 × 1,365 = 111007923832370565。
在节目中,谢尔顿问自己有多少张独特的宾果卡。根据后来的错误公式,我猜他指的是排列。换句话说,两张数字相同但位置不同的卡牌都是独一无二的。
上图展示了 Sheldon 计算 B、I、G 和 O 列的公式。他最初计算的公式是 5! × combin(15,5)。然而,他错误地将其简化为 15!/(15!-5)!。第二个感叹号不应该出现在那里,应该是 15!/(15-10)!。然而,他随后又得到了正确答案 360,360。

N 列也出现了同样的问题。公式应该是 15!/(15-4)!,而不是 15!/(15!-4)!。第二个感叹号搞砸了。
讽刺的是,在剧集的后面,谢尔顿开始痴迷于《指环王》年表中的错误,就像我痴迷于这个一样。

一个装满水的100升水箱,里面装有10公斤盐。如果我们每分钟加入10升纯净水,同时每分钟排出10升溶液,30分钟后水箱中会剩下多少盐?
让我们首先定义几个变量:
- s = 罐中盐的重量
- t = 将盐倒入水箱后的分钟数
已知每分钟流失10%的盐分。用数学语言来表达就是:
ds/dt = (-10/100) × s
让我们重新排列一下:
ds = (-10/100) × s dt
-10/s ds = dt
整合双方:
(1)-10×ln(s) = t + c
接下来,我们来求出那个令人头疼的积分常数。为了求出这个常数,我们已知当 t = 0 时 s = 10。将其代入上面的公式 (1) 中,我们得到:
-10 × ln(10) = 0 + c
所以 c = -10×ln(10)
将其代入公式 (1) 中,我们得到:
(2)-10×ln(s) = t -10×ln(10)
问题是,t=30 时,水箱里有多少盐。求解 t=30 时的 s:
-10×ln(s) = 30 -10×ln(10)。接下来将两边同时除以 -10……
ln(s) = -3 + ln(10)
s = exp(-3 + ln(10))
s = exp(-3) × exp(ln(10))
s = 指数(-3) × 10
s =~ 0.4979 公斤盐。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
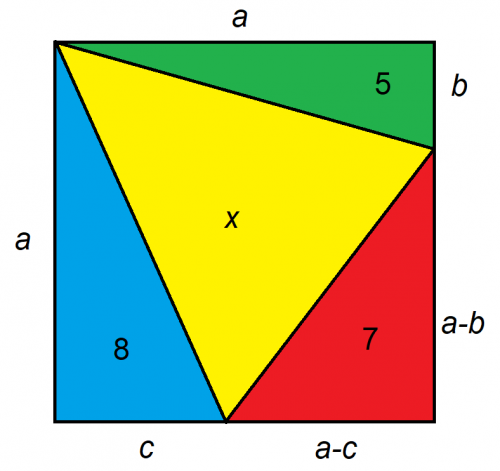
假设较大的图形是正方形,x 的面积是多少?
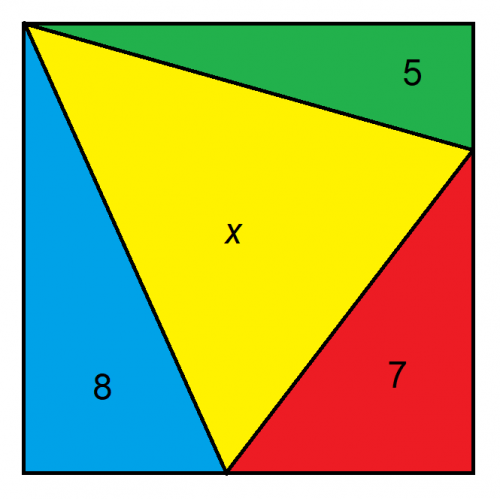
解决这类问题的关键在于如何设置它们。我建议尽量将问题简化为尽可能少的未知数。在本例中,我们可以将正方形上的未知距离表示为三个,如下所示:
处理矩形比处理三角形更容易。已知三个三角形的面积,我们可以将矩形的大小和面积都加倍。这样一来:
- ab=10
- ac=16
- (ab)(ac)=14
让我们分解 (ab)(ac):
a 2 - ab - ac + bc = 14
2-10-16 + bc = 14
(1) a2 +bc=40
让我们用 a 来表示 b 和 c,以将其归结为单个变量:
b = 10/a
c = 16/a
用这些值代替方程 (1) 中的 b 和 c:
2 + (10/a)*(16/a) = 40
a2 + 160/ a2 = 18
接下来,让我们将所有数都乘以2来去掉分母中的2 。
4 + 160 = 40 * 2
4-40 * 2 +160=0
让我们定义一个新变量 y = a 2
y 2 - 18y + 32 = 0
接下来,让我们使用二次公式求解 y:
y = (40 +/- 平方根(1600-640))/2
y = (40 +/- 平方根(960))/2
y = (40 +/- 8*sqrt(15))/2
y = 20 +/- 4 * sqrt(15)
整个正方形的面积是2 ,恰好等于 y。根据上面的公式,如果 +/- 为负,则 y = apx 4.5081,这显然是错误的,因为我们知道面积至少是 20,甚至不包括 x。因此,正方形的面积必须是 20 + 4*sqrt(15)。
给定三个三角形,其面积分别为 5+7+8=20。用正方形的总面积减去该面积,可得出 x 的面积:20 + 4*sqrt(15) - 20 = 4*sqrt(15) = apx 15.4919。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。

注意照片里我的T恤。我去看《原钻》的时候,电影院收银员夸我穿了这件T恤。为了报答她,我用这道题折磨她,只用面积分别为2、3和4的三角形。电影结束后,我去看她,她还是没解出来,但似乎在努力。于是,我在阳光海岸酒吧给她写了下面的解法。她似乎很欣赏。我觉得这位年轻女士的人生一定会很成功。
有一个 1×1 的方形飞镖靶。向靶心投掷一支飞镖,飞镖落在靶心任意位置的概率相等。飞镖落点的坐标为 (x,y),其中 x 和 y 服从 0 到 1 之间的均匀独立分布。
设 z = round(x/y)。换句话说,z = x/y,四舍五入到最接近的整数。z 为偶数的概率是多少?
了解以下提示中的无穷级数将非常有用。
[剧透=提示]莱布尼茨 π 公式指出:
1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
[/spoiler]仅需获取答案,请单击以下按钮。
单击下面的按钮获取解决方案。
[剧透=解决方案]
如果 x/y < 0.5,则该比率将向下舍入为 0 或偶数。飞镖靶上 (0,0) 和 (0.5) 所成直线左侧的任意点都将向下舍入为 0。该区域是一个直角三角形,边长为 1 又 1/2。记住,三角形的面积是 (1/2) * 底 * 高。因此,这些点向下舍入为 0 的面积为 (1/2) * (1/2) = 1/4。
图表中下一个四舍五入为偶数 2 的区域是当 1.5 < x/y < 2.5 时。该区域是一个底边为 2/3 - 2/5、高为 1 的三角形。注意,这些是 x/y 边界的倒数,因为 x 等于 1,所以我们需要反转 y。因此,四舍五入为 2 的区域是 (1/2)*(2/3 - 2/5)。
图表中下一个四舍五入为偶数 4 的区域是 3.5 < x/y < 4.5。该区域是一个底边为 2/7 - 2/9、高为 1 的三角形。因此,四舍五入为 2 的区域是 (1/2)*(2/7 - 2/9)。
图表中下一个四舍五入为下一个偶数 6 的区域是当 5.5 < x/y < 6.5 时。该区域是一个底边为 2/11 - 2/13、高为 1 的三角形。因此,四舍五入为 2 的区域是 (1/2)*(2/11 - 2/13)。
开始发现规律了吗?它是这样的:
1/4 + 1/2*(2/3 - 2/5 + 2/7 - 2/9 + 2/11 - 2/13 + ... ) =
1/4 + (1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =
让我们将 -1 移动到括号内。
5/4 + (-1 + 1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =
5/4 - (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 + ... ) =
接下来,回想一下我们上面的提示:
1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11
回到手头的问题……
5/4 - π/4 =
(5 - π) / 4 = apx。 0.464601836602552。
有趣的是,π 和 e 在数学中不断出现。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
设9x + 12x = 16x
x 是什么?
点击下面的按钮获取答案。
单击下面的按钮获取解决方案。
[剧透=解决方案]
9x + 12x = 16x =
将两边除以 9 x
1 + (12/9) x = (16/9) x
1 + (4/3) x = ((4/3) x ) 2
(1)设 u = (4/3) x
1 + u = u 2
根据二次公式...
u = (1+sqrt(5)) / 2(黄金分割率)
将其代入公式 (1) 中:
(4/3) x =(1 + 平方根(5))/ 2
对两边取对数:
x ln(4/3) = ln[(1+sqrt(5)) / 2]
x = ln[(1+sqrt(5)) / 2] / ln(4/3)
x = [ln(1+sqrt(5) - ln(2)] / [ln(4) - ln(3)] = 约 1.67272093446233。[/剧透]
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
致谢:我从Mind Your Decisions的 Presh Talwalkar 那里得到了这个问题的变体。
一位农民种了5颗苹果种子。每天,每颗种子有1/3的概率发芽。请问五棵树全部发芽的平均时间是多少?
[剧透=解决方案]
一位农民种了5颗苹果种子。每天,每颗种子有1/3的概率发芽。请问五棵树全部发芽的平均时间是多少?
我们反过来算一下。如果剩下一颗种子还没有发芽,它平均需要 1/p 天才能发芽,其中 p 是任意一天发芽的概率。由于 p = 1/3,所以平均需要 3 天才能发芽。我们称其为 t 1 = 3。
如果剩下两颗种子呢?第二天两颗种子都有 ap 2 = 1/9 的概率发芽,这样就完成了。其中一颗种子第二天发芽的概率是 2×p×q,其中 q 是不发芽的概率。因此,一颗种子发芽的概率是 2×(1/3)(2/3) = 4/9。两颗种子都不发芽的概率是 q 2 = (2/3) 2 = 4/9。我们将两颗种子的预期天数称为 t 2 。
t 2 = 1 + (4/9)×t 1 + (4/9)t 2
t 2 = (1 - (4/9)) = 1 + (4/9)×t 1
t2 = (1 + (4/9)×3) / (1 - (4/9))
t2 = (21/9) / (5/9)
t2 = (21/9) × (9/5) = 21/5 = 4.2
如果剩下三颗种子呢?有 p 3 = 1/27 的概率,它们第二天都会发芽,我们就完成了。其中一颗种子第二天发芽的概率是 3×p×q 2 = 3×(1/3)(2/3) 2 = 12/27。第二颗种子第二天发芽的概率是 3×p 2 ×q = 3×(1/3) 2 ×(2/3) = 6/27。没有种子发芽的概率是 q 3 = (2/3) 3 = 8/27。我们将拥有三颗种子的预期天数称为 t 3 。
t 3 = 1 + (6/27)t 1 + (12/27)×t 2 + (8/27)×t 3
t 3 = 1 + (6/27)×3 + (12/27)×4.2 + (8/27)×t 3
t3 × (1 - 8/27) = (1 + 18/27 + 28/15)
t 3 = (1 + 18/27 + 28/15) / (1 - 8/27) = 477/95 = 约 5.02105263
如果剩下四颗种子怎么办?有 ap 4 = 1/81 的概率,四颗种子第二天都会发芽,我们就完成了。一颗种子第二天发芽的概率是 4×p×q 3 = 4×(1/3)(2/3) 3 = 32/81。第二颗种子第二天发芽的概率是 combin(4,2)×p 2 ×q 2 = 6×(1/3) 2 ×(2/3) 2 = 24/81。第三颗种子第二天发芽的概率是 combin(4,3)×p 3 ×q = 4×(1/3) 3 ×(2/3) = 8/81。没有种子发芽的概率是 q 4 = (2/3) 4 = 16/81。我们将拥有三颗种子的预期天数称为 t 4 。
t 4 = 1 + (8/81)×t 1 + (24/81)×t 2 + (32/81)×t 3 + (16/81)×t 4
t4 = 1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263 + (16/81)× t4
t 4 = (1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263) / (1 - (16/81))
t 4 = 约 5.638056680161943319838056680。
如果剩下的五颗种子都还剩下呢?第二天,五颗种子全部发芽的概率是 p 5 = 1/243,这样我们就完成了。一颗种子第二天发芽的概率是 5×p×q 4 = 5×(1/3)(2/3) 4 = 80/243。第二颗种子第二天发芽的概率是 combin(5,2)×p 2 ×q 3 = 10×(1/3) 2 ×(2/3) 3 = 80/243。第三颗种子第二天发芽的概率是 combin(5,3)×p 3 ×q = 10×(1/3) 3 ×(2/3) 2 = 40/243。第四颗种子第二天发芽的概率是 combin(5,4)×p 4 ×q = 5×(1/3) 4 ×(2/3) = 10/243。没有种子发芽的概率是 q 5 = (2/3) 5 = 32/243。我们将有三颗种子的预期天数称为 t 5 。
t 5 = 1 + (10/243)×t 1 + (40/243)×t 2 + (80/81)×t 3 + (80/243)×t 4 + (32/243)×t 5
t5 = (1 + (10/243)× t1 + (40/243)× t2 + (80/81)× t3 + (80/243)× t4 ) / (1 - (32/243))
t5 = (1 + (10/243)×3 + (40/243)×4.2 + (80/243)×(477/95) + (80/243)×5.63805668) / (1 - (32/243))
t 5 = 约 6.131415853。
[/spoiler]该问题改编自Mind Your Decisions的 Presh Talwalkar 提出的类似问题。
我有一个由两部分组成的问题。
对于第 1 部分,给出:- x + y + z = 1
- x^2 + y^2 + z^2 = 4
- x^3 + y^3 + z^3 = 9
x^4 + y^4 + z^4 是多少?
对于第二部分,当出现以下情况时,一般情况的答案是什么:
- x + y + z = a
- x^2 + y^2 + z^2 = b
- x^3 + y^3 + z^3 = c
一种微生物,我们称之为 Covid-20,可以随时产生新的微生物。特定微生物在任何给定时间从特定亲本微生物产卵的概率始终相同,无论距离上次产卵的时间如何。同一种微生物产卵的平均间隔为一天。用数学术语来说,同一种微生物产卵的预期间隔遵循指数分布,平均值为一天。
一旦微生物进入您的肺部,预计七天后您的肺部微生物数量是多少?
点击下面的按钮获取答案。
单击下面的按钮获取解决方案。
[剧透=解决方案]
这个解法需要一个常微分方程。如果你的数学教育还没达到这个程度,你就无法理解。
让:
m = Covid-20 微生物数量
t = 时间,以天为单位
由于每个微生物平均每天产生一个新微生物,因此 m 个微生物平均每天会产生 m 个新微生物。换句话说,在任何给定时间 t,微生物 (m) 的增长率可以写成:
dm/dt = m。
我不确定表达这一点的正确方法,但将 dt 分开到右侧:
dm = m dt。
将两边除以 m:
1/m dm = 1 dt。
将两边积分:
ln(m) = t + C,其中 C 是积分常数。
已知在时间 0 时有 1 个微生物。换句话说,当 t = 0 时,m = 1。我们可以将这些值代入上面的公式来求解 C:
ln(1) = 0 + C
0 = 0 + C
C = 0。
我们现在有 ln(m) = t。
对两边取 exp():
m = e t
因此,在时间 t=7 时,将有 e 7 = 约 1096.6332 个微生物。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
在一家老式西部酒吧里,一场关于纸牌游戏的争吵逐渐升级为附近所有的牛仔都拔出枪互相射击。
当硝烟最终散去时,90%的牛仔腿部中弹,85%的牛仔手臂中弹,80%的牛仔腹部中弹,75%的牛仔头部中弹。令人惊讶的是,只有四种伤势都达到的牛仔在这场激烈的枪战中阵亡。
最终被安葬的牛仔的最小可能百分比是多少?
[剧透=向导解决方案]
首先,向 90% 的牛仔的腿部开枪。
接下来,射击手臂上剩下的10%。你还有75%的子弹可以射击手臂,所以从那些已经中过腿的子弹中抽取。
所以,我们现在处于:
仅腿部 15% (90% - 75%)
仅武装 10%
两者均为 75%
都不是 0%
总腿长:90%
总臂长:85%
接下来,我们来看看腹部受伤的情况(80%)。拍摄那 25% 的受伤者,他们腹部只有一处受伤。我们还有 80% - 25% = 55% 的受伤者可以拍摄。我们会从腹部两处受伤的人员中抽取这 55%。所以现在我们得出:
腿和内脏 15%
手臂和内脏 10%
腿部和手臂 20% (75% - 55%)
三者皆有 55%
一次受伤 0%
零伤害 0%
最后,考虑头部受伤的75%。首先,射击恰好两次受伤的45%。我们还剩30%,所以从三次受伤的55%中抽取。这样就剩下:
头、腿和内脏 15%
头部、手臂和内脏 10%
头部、腿部和手臂 20%
腿部、手臂和肠道:25% (55% - 30%)
全部四个 30%
零伤害 0%
一次受伤 0%
两次受伤 0%
[剧透=CharliePatrick 解决方案]
假设有20个牛仔。我们选择这个数字是因为所有涉及的概率都能被5%整除,而20的5%等于1。
把他们排成一排。然后,从左边开始,射杀其中90%的人,也就是18人,射中他们的腿部。然后画一个图表,上面一行写牛仔的编号,左边一列写每个人的受伤总数,如下图所示。
| 受伤 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 十三 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | ||
| 2 | ||||||||||||||||||||
| 3 | ||||||||||||||||||||
| 4 | ||||||||||||||||||||
| 全部的 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
接下来,你需要射中85%的子弹,也就是17发子弹击中手臂。从两个腿部没有中弹的牛仔开始。你还剩15发子弹。回到左边的牛仔,沿着这一排向下移动,射中腿部的子弹总数达到15发。你的伤害卡应该是这样的:
| 受伤 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 十三 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 一个 | 一个 |
| 2 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | |||||
| 3 | ||||||||||||||||||||
| 4 | ||||||||||||||||||||
| 全部的 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 |
接下来,你需要射击 80%,也就是腹部 16 发子弹。从五个只受过一次伤的牛仔开始。你还有 11 发子弹要打。回到左边的牛仔,沿着这一排向下移动,总共射击 11 发已经受过两次伤的牛仔。你的伤势卡应该是这样的:
| 受伤 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 十三 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 一个 | 一个 |
| 2 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 格 | 格 | 格 | 格 | 格 |
| 3 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | |||||||||
| 4 | ||||||||||||||||||||
| 全部的 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
接下来,你需要射击75%,也就是头部15个。从9个只被射中两次的牛仔开始。你还有6个牛仔需要射击。回到左边的牛仔,沿着这一排向下移动,总共射击6个已经被射中三次的牛仔。你的伤害卡应该是这样的:
| 受伤 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 十三 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 左 | 一个 | 一个 |
| 2 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 一个 | 格 | 格 | 格 | 格 | 格 |
| 3 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | 格 | 哈 | 哈 | 哈 | 哈 | 哈 | 哈 | 哈 | 哈 | 哈 |
| 4 | 哈 | 哈 | 哈 | 哈 | 哈 | 哈 | ||||||||||||||
| 全部的 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
可以看到,6名牛仔被枪击四次,14名牛仔被枪击三次。因此,最多只能受三次伤的比例是14/20 = 70%。
对于一般情况,如果四个概率分别是 a、b、c 和 d,那么可以存活的最大比率是 1-(a+b+c+d),只要 a+b+c+d >=3 且 a+b+c+d <=4。
我要感谢并赞扬维加斯巫师论坛成员 CharliePatrick 提供的解决方案。
[/spoiler]从这篇文章开始,这个问题就在我的论坛中被提出并讨论过。
一只青蛙可以跳一英尺或两英尺。青蛙多次跳跃,总共跳了十英尺,并且始终向前。考虑到跳跃距离和顺序,有多少种不同的方法可以做到这一点?
[剧透=解决方案]
- 如果青蛙只需要跳一只脚,显然只有一种方法。记住,青蛙不能超出目标。
- 如果青蛙需要跳两英尺,则有两种方法可以实现 - (1)1 英尺和 1 英尺,或(2)2 英尺。
如果青蛙需要跳三英尺,那么在最后一次跳跃之前,它可以离青蛙一英尺,也可以离青蛙两英尺。有一种方式可以离青蛙两英尺,如步骤1所示;还有两种方式可以离青蛙一英尺,如步骤2所示。因此,跳三英尺有三种方式。这也很容易验证:(1) 1+1+1,(2) 1+2,(3) 2+1。
如果青蛙需要跳四英尺,那么在最后一次跳跃之前,它可以离青蛙两英尺或三英尺远。如步骤2所示,有两种方法可以离青蛙两英尺远,如步骤3所示,有三种方法可以离青蛙一英尺远。因此,跳四英尺远的方法有五种。这也很容易验证:(1) 1+1+1+1,(2) 1+1+2,(3) 1+2+1,(4) 2+1+1,(5) 2+2。
如果青蛙需要跳5英尺,那么它在最后一次跳跃前可以距离目标3英尺或4英尺。距离目标2英尺有3种方法,如步骤3所示;距离目标1英尺有5种方法,如步骤4所示。因此,跳5英尺有3+5=8种方法。这也很容易验证:(1) 1+1+1+1+1,(2) 1+1+1+2,(3) 1+1+2+1,(4) 1+2+1+1,(5) 2+1+1+1,(6) 2+2+1,(7) 2+1+2,(8) 1+2+2。
你开始看出规律了吗?这就是斐波那契数列。按照同样的逻辑,青蛙一共可以跳出10英尺,一共有89种方法。使用 1、5、10、25、50 美分和 1 美元的标准美国硬币,有多少种方法可以兑换 1 美元?
设 a(x) = 仅使用一分硬币和五分硬币赚取 x 美分的方法数,其中 x 可以被 5 整除。
a(x) = 1+(x/5)
换句话说,方法数就是找零中可能的五分硬币的数量,范围从 0 到 x/5。
设 b(x) = 仅使用 1 美分、5 美分和 10 美分硬币赚取 x 美分的方法数,其中 x 可以被 5 整除。
b(0)=1
b(5)=2
b(x) = a(x) + b(x-10),其中 x>=10。
用简单的英语来说,赚取 x 美分的方法数是 (1) b(x-10) = 通过在每种方式中添加一角硬币赚取 x-10 美分的方法数和 (2) a(x) = 不使用一角硬币的方法数之和。
令 c(x) = 赚取 x 美分的方法数,仅使用 1 分硬币、5 分硬币、10 分硬币和 25 美分硬币,其中 x 可以被 25 整除。
c(0) = 1
c(x) = b(x) + c(x-25),其中 x>=25。
用简单的英语来说,赚取 x 美分的方法数是 (1) c(x-25) = 通过在每种方法上加 25 美分赚取 x-25 美分的方法数,以及 (2) b(x) = 不使用 25 美分赚取的方法数。
令 d(x) = 赚取 x 美分的方法数,仅使用 1 美分、5 美分、10 美分、25 美分和半美元,其中 x 可以被 50 整除。
d(0) = 1
d(x) = c(x) + d(x-50),其中 x>=50。
用简单的英语来说,得到 x 美分的方法数是 (1) d(x-50) = 通过在每种方法上加半美元得到 x-50 美分的方法数和 (2) c(x) = 不使用半美元的方法数之和。
下表显示了 x = 5 至 100 的这些值。
做出改变的方法
| x | 斧头) | b(x) | c(x) | d(x) |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | |
| 5 | 2 | 2 | 0 | |
| 10 | 3 | 4 | 0 | |
| 15 | 4 | 6 | 0 | |
| 20 | 5 | 9 | 0 | |
| 二十五 | 6 | 12 | 十三 | |
| 三十 | 7 | 16 | 0 | |
| 三十五 | 8 | 20 | 0 | |
| 40 | 9 | 二十五 | 0 | |
| 45 | 10 | 三十 | 0 | |
| 50 | 11 | 三十六 | 49 | 50 |
| 55 | 12 | 四十二 | 0 | |
| 60 | 十三 | 49 | 0 | |
| 65 | 14 | 56 | 0 | |
| 70 | 15 | 64 | 0 | |
| 75 | 16 | 72 | 121 | |
| 80 | 17 | 81 | 0 | |
| 85 | 18 | 90 | 0 | |
| 90 | 19 | 100 | 0 | |
| 95 | 20 | 110 | 0 | |
| 100 | 21 | 121 | 242 | 292 |
最后,加上 1 美元硬币,答案就是 292+1 = 293。
[/spoiler]这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
有无数个灯泡,全部关闭。灯泡开启的时间间隔服从指数分布*,平均值为1天。灯泡开启后,其预期寿命也服从指数分布,平均值为1天。
第一个灯泡烧坏的平均时间是多少?
*:遵循指数分布的随机事件具有无记忆特性,即过去的事情并不重要。换句话说,单个事件永远不会过期,其发生的概率也始终相同。
平均而言,第一盏灯泡需要一天的时间才能亮起来。
从那时开始,平均需要半天时间才能发生下一个重大事件,要么是新灯泡亮了,要么是第一个灯泡烧坏了。我们将等待时间加到半天,这样就得到了 1 + (1/2) = 1.5 天。
第二个事件是打开第二个灯泡的概率是1/2。在这种情况下,距离下一个重要事件(前两个灯泡烧坏或打开新灯泡)有1/3天的等待时间。因此,将1/2(发生到这一步的概率)乘以1/3,等于1/6,加到等待时间上。这样,我们得到的不是1.5 + 1/6 = 5/3 = 1.66667天。
第三个重要事件是第三个灯泡亮起的概率为 (1/2)*(1/3) = 1/6。在这种情况下,距离下一个重要事件(前三个灯泡烧坏或新灯泡亮起)有 1/4 天的等待时间。因此,将 1/6(发生到这一步的概率)乘以 1/4,等于 1/24,加到等待时间上。这样,我们得到的不是 5/3 + 1/24 = 41/24 = 1.7083 天。
按照这种模式,答案是 (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...
常识应该是 e = (1/0!) + (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...
唯一的区别是我们的答案少了 1/0! 这个因子。因此,答案是 e - 1/0! = e - 1 = 约 1.7182818……
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
A、B、C、D 均为不同的正整数。
A < B < C < D
找到最大的 D,以便
1/A + 1/B + 1/C + 1/D = 1
答案是42。A、B、C分别为2、3、7。
1/2 + 1/3 + 1/7 + 1/42 = 1。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
看完《后翼弃兵》后,我注意到节目里没有一盘棋以平局结束。我以为高水平的国际象棋比赛有很多平局。对于大师级的国际象棋来说,平局的概率是多少?
根据 ChessBase.com 上的文章《国际象棋中的和棋次数增加了吗?》 ,作者周奇宇指出,在 78,468 场评分 2600 分或以上的选手(达到 2500 分才能成为大师)的比赛中,结果如下:
- 黑棋胜率:18.0%
- 白棋胜率:28.9%
- 平局:53.1%
有一块 5x5 的钉板和 3 个钉子。三个随机放置的钉子形成三角形的概率是多少?
[剧透=解决方案]
首先,对于钉子来说,有 combin(25,3) = 2,300 种可能的组合。
这些组合中有多少种可以组成三角形?让我们用这个棋盘来帮忙:
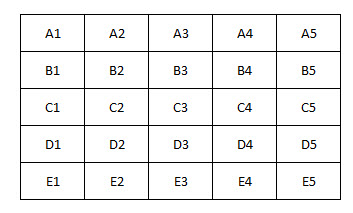
首先,棋盘有五行、五列和两条对角线。对于其中任意一条对角线,棋子排列成一条直线的方式有 (5,3) = 10 种组合方式。因此,这样一共有 12*10 = 120 种组合方式。
其次,有四种方法可以将一行/列的中心方块连接到相邻行/列的中心方块。换句话说,这三种放置方式:
- A3、B4、C5
- C5、D4、E3
- E3、D2、C1
- C1、B2、A3
所以,现在是 120 + 4 = 124
第三,有四条不同的对角线,即四个空间:
- A2、B3、C4、D5
- B5、C4、D3、E2
- E4、D3、C2、B1
- D1、C2、B3、A4
对于每个棋子,有(4,3)=4种组合方式来放置三个棋子。这样一来,棋子总数就增加了4*4 = 16。
我们现在有 124+16 = 140
第四,考虑一下国际象棋中骑士的移动方式,在2x1的L形棋盘中。骑士在每个角上有两种移动方式。在所有这些方式中,骑士都可以沿着第一步形成的直线再次移动。所以,还有4*2 = 8种移动方式:
- A1、C2、E3 A1、B3、C5
- A5、B3、C1
- A5、C4、E3
- E5、C4、A3
- E5、D3、C1
- E1、D3、C5
- E1、C2、A3
还有四条这样的骑士线穿过中心:
- A2、C3、E4
- A4、C3、E2
- B5、C3、D1
- D5、C3、B1
加上 12 条骑士线,我们得到 140+12= 152
如果总共有 2,300 种组合,其中 152 种形成线条,那么 2300-152 = 2,148 种组合不会形成线条,因此会形成三角形。
因此,我们的答案是 2,148/2,300 = 93.39%。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
您获得:
- 当时,一架飞机距离一枚正在发射的地对空导弹正上方八英里。
- 飞机始终沿直线飞行。
- 飞机以每小时 600 英里的速度飞行。
- 导弹飞行速度为每小时2000英里。
- 导弹总是以直接面向飞机的角度飞行。
问题:
- 飞机在被导弹击中之前会飞行多远?
- 导弹要花多长时间才能击中飞机?
- 导弹的飞行路径有多长?
- 飞机在被导弹击中之前会飞行多远?= 240/91 英里
- 导弹击中飞机需要多长时间?= 2/455 小时
- 导弹飞行距离是多少?= 800/91 英里
这是我的解决方案(PDF)。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
认为:
- 90%的公众佩戴口罩。
- 戴口罩的人感染冠状病毒的概率为 1%,不戴口罩的人感染冠状病毒的概率为 3%。
随机选择一名冠状病毒患者。他戴口罩的概率是多少?
这是一个经典的贝叶斯条件概率问题。
答案是概率(某人戴口罩并感染冠状病毒)/概率(某人感染冠状病毒)=
(0.9*0.01)/(0.9*0.01+0.1*0.03)= 75%。
正方形中间有一只蚂蚁,它距离左上角17英寸,距离右上角20英寸,距离右下角13英寸。
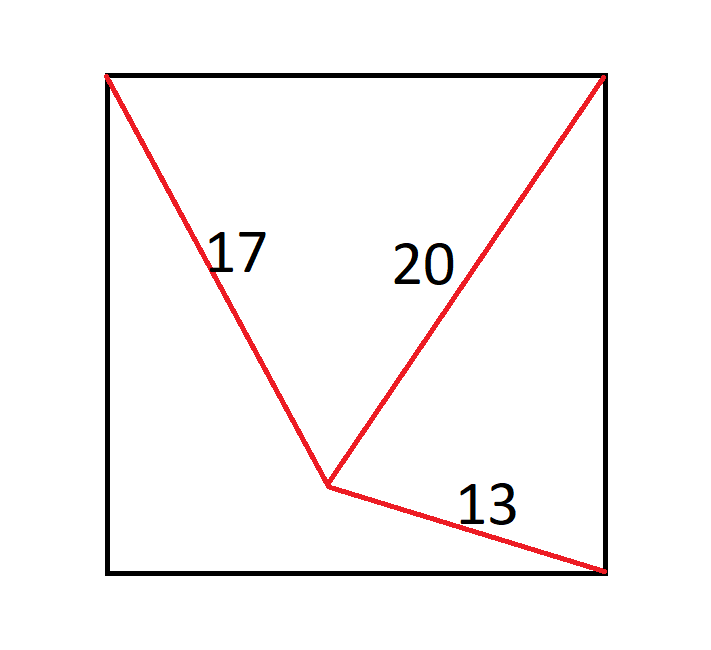
这个正方形有多大?
[剧透=有用的公式] c^2 = a^2 + b^2 -2ab*cos(c)
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
[剧透=解决方案]
首先,将三角形ABE旋转90度,形成一个新的三角形BDF。
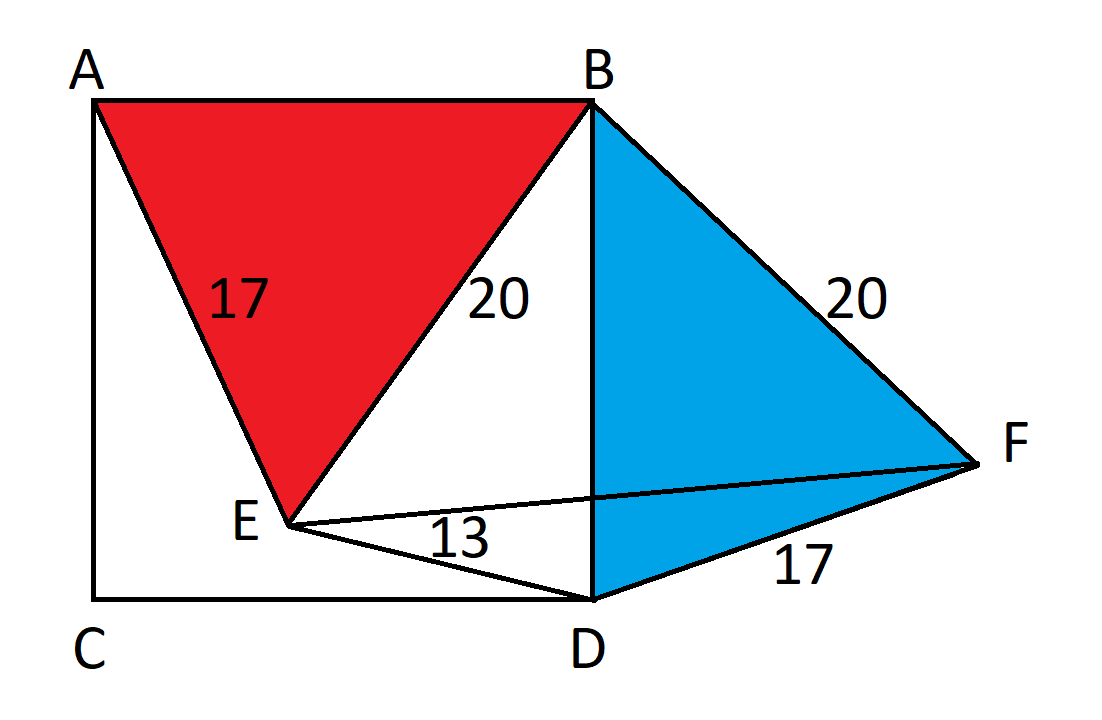
由于三角形旋转了90度,根据定义,角EBF=90。根据勾股定理,EF = 20*sqrt(2)。
根据余弦定律:17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF)。
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680。
cos(DEF) = 17*sqrt(2)/26。
回想一下,sin^2(x) + cos^2(x) = 1。让我们用它来求解 sin(DEF)。
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
接下来,考虑角度 BED。
角度 BED = 角度 BEF + 角度 FED。
我们知道 EBF 是 90 度,并且是一个等腰三角形。这样一来,角 BEF 就是 45 度。
因此,角度 BED = 45 度 + 角度 FED。
回想一下,cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)。
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
让我们再次应用余弦定律,这次针对三角形 BED。
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD 是所讨论正方形的边长,因此 BD^2 是该正方形的面积,我们已经表明其面积为 369。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
你是一名烟火技师,负责游乐园的夜间烟火表演。你收到了一些来自欧洲的新型烟花,正在测试其中一枚,以便让它与表演的音乐同步。
烟花火箭以4米²的恒定加速度垂直向上发射,直至化学燃料耗尽。随后,其上升速度在重力作用下减缓,直至达到138米的最大高度并爆炸。
假设没有空气阻力,重力加速度为每秒9.8米,火箭需要多长时间才能达到最大高度?
[剧透=解决方案]
让:
t = 火箭燃料耗尽后的时间。
r = 火箭燃料持续的时间。
我将用向上的方向来表示加速度。因此,火箭燃料燃尽后的加速度是-9.8。
提醒一下,加速度的积分是速度,速度的积分是位置。我们假设位置是相对于地面的。
当火箭首次发射时,我们已知加速度为 4。
取积分,r秒后火箭的速度等于4r。
对速度进行积分可以得出 2r 2的 r 秒后火箭的位置。
现在让我们看看火箭燃料烧完后会发生什么。
我们已知重力加速度为-9.8。
t时刻的重力速度为-9.8t。然而,它从火箭向上也有4r的速度。
设 v(t) = 时间 t 时的速度
v(t) = -9.8t + 4r
当 v(t) = 0 时,火箭将达到最大高度。让我们来解决这个问题。
v(t) = 0 = -9.8t + 4r
4r = 9.8t
t = 40/98 r = 20r/49。
换句话说,无论火箭燃料持续多长时间,火箭都会在其中的 20/49 时间内继续飞行。
我们还知道,在达到的最大高度行驶的距离是 138。
让我们对 v(t) 进行积分,得到行进距离的公式,我们将其称为 d(t)。
d(t) = -4.9t 2 + 4rt + c,其中 c 是积分常数。
正如我们已经证明的,当燃料耗尽时,火箭的行程为 2r 2 ,因此这必定是积分常数。由此可得:
d(t) = -4.9t² + 4rt + 2r²
我们知道在时间 20r/49 时达到了最大高度 138,因此让我们将 t=20r/49 代入方程来求解 r:
d((20r/49) = -4.9((20r/49) 2 + 4r(20r/49) + 2r 2 = 138
r2 *(-1960/2401 + 80/49 + 2) = 138
r2 = 49
r = 7
因此,火箭燃料可持续使用七秒。
我们已经知道火箭在这段时间内继续上升了 20/49,也就是 140/49 = 约 2.8571 秒。
因此,从发射到最大速度的时间为 7 + 140/49 = 483/49 = 约 9.8571 秒
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
要使两个骰子的总点数从 2 到 12 不等,预计需要掷多少次?请使用微积分来解答。
[剧透=解决方案]
回想一下,掷出总数为 2 的概率是 1/36。在 t 次掷骰中,预期掷出总数为 2 的次数为 t/36。假设掷骰间隔时间呈指数分布,平均值为 t/36。泊松分布告诉我们,掷出总数为 2 的次数为零的概率为 exp(-t/36)。
回想一下,掷出总数 3 的概率是 2/36 = 1/18。按照同样的逻辑,泊松分布告诉我们,掷出总数 3 且掷出次数为零的概率是 exp(-t/18)。
回想一下,掷出总数 4 的概率是 3/36 = 1/12。按照同样的逻辑,泊松分布告诉我们,掷出总数 4 且掷出次数为零的概率是 exp(-t/12)。
回想一下,掷出总数 5 的概率是 4/36 = 1/9。按照同样的逻辑,泊松分布告诉我们,掷出总数 5 且掷出次数为零的概率是 exp(-t/9)。
回想一下,掷出总点数 6 的概率是 5/36。按照同样的逻辑,泊松分布告诉我们,掷出总点数 6 且掷出零点的概率是 exp(-5t/36)。
回想一下,掷出总数 7 的概率是 6/36 = 1/6。按照同样的逻辑,泊松分布告诉我们,掷出总数 7 且掷出零次的概率是 exp(-t/6)。
8 到 12 的概率与 2 到 6 的概率相同。
因此,每个总数中的 t 个单位至少被滚动一次的概率是:
(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
在 t 个时间单位内至少 total 未滚动的概率为 1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
为了得到没有至少一个总数的预期时间,我们将上述函数从 0 积分到无穷大。
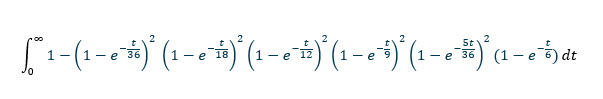
积分计算器(我推荐这个)可以轻松解决这个问题,因为 769767316159/12574325400 = apx。61.2173847639572 卷。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
长方体是由单位正方形组成的三维块。
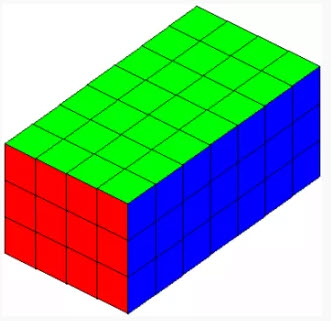
一个 a × b × c 的长方体由 abc 个相同的单位立方体构成,就像一个 3x3x3 的魔方。将立方体分成两种互斥的类型。外部立方体是构成长方体各个面的立方体;内部立方体是完全封闭的。例如,图中的长方体有 74 个外部立方体和 10 个内部立方体。
给出所有长方体的尺寸,使得外部立方体的数量等于内部立方体的数量。
- 5 x 13 x 132
- 5 x 14 x 72
- 5 x 15 x 52
- 5 x 16 x 42
- 5 x 17 x 36
- 5 x 18 x 32
- 5 x 20 x 27
- 5 x 22 x 24
- 6 x 9 x 56
- 6 x 10 x 32
- 6 x 11 x 24
- 6×12×20
- 6 x 14 x 16
- 7×7×100
- 7×8×30
- 7×9×20
- 7 x 10 x 16
- 8×8×18
- 8 x 9 x 14
- 8 x 10 x 12
我在Wizard of Vegas论坛上提出并讨论了这个问题。
设 0 < a < b,a^b 和 b^a 哪个更大?
答案具体取决于 a 和 b,但两个经验法则可以解决大多数情况。
如果 a > e,则 a^b > b^a
如果 b < e,则 a^b < b^a
如果 a < e 且 b > e,则没有足够的信息来确定。
这是解决方案(PDF)。
一枚手榴弹被扔进一个无底洞。平均而言,手榴弹会在六秒内爆炸。爆炸前的时间具有无记忆性,即任何特定时刻爆炸的概率始终相同,且与拉开保险栓后的时间长短无关。换句话说,它的寿命遵循指数分布。假设加速度为每秒32英尺。
假设有一档游戏节目,参赛者都是自私的,而且都是逻辑思维完美的人。规则如下。
- 主持人将 1,000,000 美元放在两位参赛者之间的桌子上。
- 要求参赛者 A 就如何在两位参赛者之间分配资金提出建议。
- 参赛者 B 将被要求接受或拒绝该建议。
- 如果参赛者 B 接受该建议,那么他们就按照建议分配钱款,游戏结束。
- 如果参赛者 B 拒绝该建议,那么主持人将扣除当前桌上 10% 的金额。
- 然后主持人会要求参赛者 B 提出建议,参赛者 A 有同样的机会接受或拒绝该建议。
- 如果选手A接受建议,两人就按此比例分配,游戏结束。如果选手A拒绝,主持人会从剩余金额中抽取10%。然后回到步骤2,重复此操作,直到有人接受建议。
问题是,参赛者 A 在第一轮比赛中应该建议如何分配资金?
他应该建议自己留下10/19的钱,减去1美分,然后给B 9/19的钱,再加1美分。换句话说:
答:526,315.78 美元
B:473,684.22美元
[剧透=解决方案]
关键是 A 应该让 B 尽可能接近无差异点。
我们将底池与另一位玩家的比例设为r。如果B接受报价,他将获得r×1,000,000美元。
如果B拒绝了邀请,那么主持人将获得10%的提成。之后,B将获得位置优势,并会将r份额分给参赛者A,自己则保留1-r。
求解r...
r×1,000,000 美元 = (1-r)×900,000 美元。
r×1,900,000 美元 = 900,000 美元。
r = 900,000 美元/1,900,000 美元 = 9/19。
A 不希望 B 完全无动于衷,以免 A 随意选择,让主持人有机会从中捞取好处。所以,A 应该把多余的 1 美分扔给 B,并给他 (9/19) × 1,000,000 美元 + 0.01 美元 = 473,684.22 美元。
答:526,315.78 美元
B:473,684.22美元
我在Wizard of Vegas论坛上提出并讨论了这个问题。
两座城市,方特勒罗伊和索思沃思,横跨一条海峡。两艘渡轮整天往返于两座城市之间。两艘渡轮以不同的速度航行。它们同时从两座城市出发。
他们第一次过河是在距离Southworth 5英里的地方。第二次过河是在距离Fauntleroy 3英里的地方。假设没有时间装卸货物,但两辆车都立即掉头。同时假设他们沿直线行驶。
这两个城市相距多远?
令t2 = 第二次穿越的时间
r = 渡轮最初离开 Fauntleroy 的速度与渡轮最初离开 Southworth 的速度之比。
c = 两座城市之间的海峡距离。
已知他们第一次过河的地点距离Southworth有5英里。用公式来表达:
c-5 = r*t 1
5 = t 1
使 t 1相等,我们得到:
c-5 = 5r,或 r = (c-5)/5
我们还已知,他们第二次过河时,距离方特勒罗伊有3英里。用公式来表达:
3c-3 = r*t 2
c+3 = t2
使 t 2相等,我们得到:
2c - 3 = r*(c+3)
代入 r=(c-5)/5
2c-3 = [(c-5)/5] * (c+3)
10c - 15 = c^2 - 2c - 15
c^2 - 12c = 0 c - 12 = 0 c = 12
因此,该水道长 12 英里。
下图中蓝色区域的面积是多少?
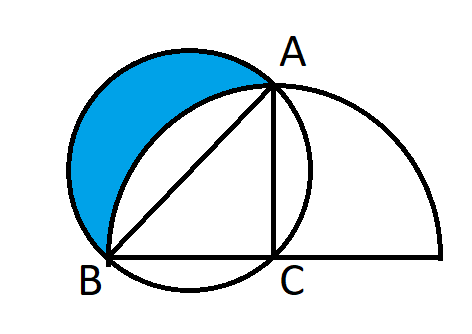
在国际象棋锦标赛中,每位选手与其他每位选手进行一场比赛。每位选手每赢一局得1分,每平一局得0.5分,每输一局得0分。
比赛结束时,可以看到所有参赛者都获得了不同的分数,并且得分排名的最后一名参赛者击败了前三名的参赛者。
那么,参加比赛的参赛者最少有多少人呢?
[剧透=解决方案]
我们将玩家人数称为 n。
我估计垫底的选手只赢过前三名选手三场,其他比赛都输了。所以他得3分。
然后,我计算出每个后续玩家的分数,按排名顺序排列,比前一个玩家高出 0.5 分。这样,排名最高的玩家将获得 3+(n-1)/2 分。
将 3 与 3+(n-1)/2 相加,每一步增加 1/2 个点,得到 (((n+5)*(n+6)/2)-15)/2。
n 名玩家总共进行 n*(n-1)/2 局游戏,其中每人与其他玩家各玩一次。每局游戏产生 1 分,这也是所有玩家获得的总分。
然后求解 n:
(((n+5)*(n+6)/2)-15)/2 = n*(n-1)/2
((n+5)*(n+6)/2)-15 = n*(n-1)
(n+5)*(n+6)/2 = n*(n-1) + 15
(n+5)*(n+6) = 2*n*(n-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
n^2 + 11n = 2n^2 - 2n
n + 11 = 2n-2
n=13
下表展示了这种情况可能发生的一种情况。表格主体部分显示了全部78场比赛的获胜者。
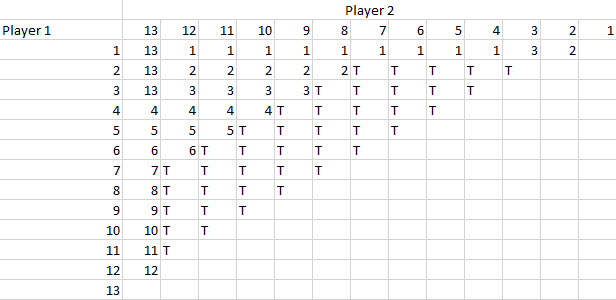
下表显示了每位球员的得分。
球员总得分
| 玩家 | 积分 |
|---|---|
| 十三 | 3 |
| 12 | 3.5 |
| 11 | 4 |
| 10 | 4.5 |
| 9 | 5 |
| 8 | 5.5 |
| 7 | 6 |
| 6 | 6.5 |
| 5 | 7 |
| 4 | 7.5 |
| 3 | 8 |
| 2 | 8.5 |
| 1 | 9 |
我在Wizard of Vegas论坛上提出并讨论了这个问题。
哪种堆放炮弹的方法更有效?是像埃及金字塔那样堆放方形底座的金字塔,还是堆放成三角形,形成四面体?


以下是读者可能会发现有用的几个公式:
向下滚动查看我的答案和解决方案。
我假设你所说的“高效”是指炮弹之间浪费的空间最少。
为了简单起见,为了定义每个金字塔的体积,我们用位于金字塔角的球体中心点作为定义。设 n 为每个金字塔底部每侧炮弹的数量。
我们先来看一下方形底座的金字塔。
整个金字塔的炮弹数量为1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + ... + n 2 = n*(n+1)*(2n+1)/6。
接下来,我们来求这个底边为 n 的正方形金字塔的高度。如图所示,除正方形底边外,其他边都是等边三角形。因此,斜高也为 n。底边一角到对角的距离为 n*sqrt(2)。因此,底边一角到底边中心的距离为 n*sqrt(2)/2。设高度为 h。考虑由高度、底边一角到底边中心的距离以及斜高构成的直角三角形。
h 2 + (n*sqrt(2)/2) 2 = n 2
h = n*sqrt(2)/2。
回想一下,金字塔的体积是底面*高/3。因此,金字塔的体积为:
n 2 * n* sqrt(2)/2 * (1/3) = n 3 *sqrt(2)/6。因此,球与体积的比率为 [n*(n+1)*(2n+1)/6] / [n 3 *sqrt(2)/6] = sqrt(2)*n*(n+1)*(2n+1)/(2*n 3 ) = sqrt(2)*(n+1)*(2n+1)/(2*n 2 )
接下来我们看一下三角形底座的金字塔。
整个金字塔的炮弹数量为1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6。
接下来,我们来求底面积。回想一下,30°-60°-90°三角形的边长分别与1/2、sqrt(3)/2和1成比例。由此不难得出,边长为n的等边三角形的高是n*sqrt(3)/2。这样,底面积就是n的2 *sqrt(3)/4。
底面一个角到底面中心的距离是 sqrt(3)/3。已知该距离以及金字塔的斜高 1,我们可以使用勾股定理求出金字塔的高度,即 sqrt(6)/3。
现在我们可以找到金字塔的体积,即底面*高度/3 = (n 2 *sqrt(3)/4) * (n*sqrt(6)/3) * (1/3) = n 3 *sqrt(18)/36 = n 3 *sqrt(2)/12。
因此,球与体积的比率为 [n*(n+1)*(n+2)/6] / [n 3 *sqrt(2)/12] = sqrt(2)*n*(n+1)*(2n+1)/(2*n 3 ) = sqrt(2)*(n+1)*(n+2)/n 2
以下是球与体积比率的比较:
- 平方底:sqrt(2)*(n+1)*(2n+1)/(2*n 2 )
- 三角形底边:sqrt(2)*(n+1)*(n+2)/n 2
我们将两个比率除以 sqrt(2)*(n+1)/n 2 :
- 方底:(2n+1)/2 = n + 0.5
- 三角形底数:n+2
随着 n 的增大,两个金字塔的炮弹数量与体积之比都会趋近于 n。换句话说,炮弹数量越多,它们的效率就越接近。
给定一个炮弹的体积,两个金字塔的效率(定义为炮弹体积与总体积的比率)接近 pi*sqrt(2)/6 =~ apx. 74.05%。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
对于任意给定的大数,该数附近的素数之间的平均距离是多少?此外,小于该数的素数有多少个?
对于任意大数 n 附近的素数之间的平均距离,一个非常好的估计方法是 ln(n)。这个估计器的精度令人惊叹。
作为佐证,下表列出了前 1500 万个素数的范围,以百万为一组。该表列出了素数之间范围内的平均距离以及平均距离的估计值。该估计值是该范围内最大和最小素数平均值的自然对数。例如,对于第 15 组一百万个素数,其值为 ln((256,203,221+275,604,541)/2)。
素数之间的平均距离
| 第一总理 在范围内 | 最后的素数 在范围内 | 素数 在范围内 | 平均距离 | 估计 | |
|---|---|---|---|---|---|
| 2 | 15,485,863 | 1,000,000 | 15.485861 | 15.86229105 | |
| 15,485,867 | 32,452,843 | 1,000,000 | 16.966976 | 16.9922867 | |
| 32,452,867 | 49,979,687 | 1,000,000 | 17.52682 | 17.53434381 | |
| 49,979,693 | 67,867,967 | 1,000,000 | 17.888274 | 17.89175615 | |
| 67,867,979 | 86,028,121 | 1,000,000 | 18.160142 | 18.15864108 | |
| 86,028,157 | 104,395,301 | 1,000,000 | 18.367144 | 18.3716137 | |
| 104,395,303 | 122,949,823 | 1,000,000 | 18.55452 | 18.54883262 | |
| 122,949,829 | 141,650,939 | 1,000,000 | 18.70111 | 18.70058553 | |
| 141,650,963 | 160,481,183 | 1,000,000 | 18.83022 | 18.83322787 | |
| 160,481,219 | 179,424,673 | 1,000,000 | 18.943454 | 18.95103217 | |
| 179,424,691 | 198,491,317 | 1,000,000 | 19.066626 | 19.05703535 | |
| 198,491,329 | 217,645,177 | 1,000,000 | 19.153848 | 19.15337672 | |
| 217,645,199 | 236,887,691 | 1,000,000 | 19.242492 | 19.24163365 | |
| 236,887,699 | 256,203,161 | 1,000,000 | 19.315462 | 19.32305683 | |
| 256,203,221 | 275,604,541 | 1,000,000 | 19.40132 | 19.39864545 |
资料来源:Prime Pages 上的Primes 之间的差距。
要计算任意给定数下的素数个数,我们可以先对 ln(n) 的平均距离估计值求积分。这样就能得到任意数 n 以内的素数之间平均距离的总和。
f(n)=ln(n) 的积分是多少?回想一下分部积分法告诉我们:
f(n)*g'(n) 的积分 dn = f(n)*g(n) - (f'(n)*g(n)) 的积分 dn
设 f(n)=ln(n) 且 g'(n)=1。则 f'(n)=1/n 且 g(n)=n。因此,ln(n) 的积分为 ln(n)*n - ((1/n)*n) 的积分 = ln(n)*n - n = n*(ln(n)-1)
如果我们将 n*(ln(n)-1) 除以 n,我们就能得到从 2 到 n 范围内素数之间的平均距离。这个距离就是 ln(n)-1。
如果我们将 n 除以素数之间的平均距离,我们会得到 n 以下素数的平均数量,等于 n/(ln(n)-1)。
作为证据,下表列出了各种大数下的素数个数及其估计值。Excel 只允许 15 位有效数字,请谅解。拜托,谁能制作一个能处理更多数字的电子表格吧。
素数之间的平均距离
| n | n 以下的素数 | n/(ln(n)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 二十五 | 二十八 |
| 1,000 | 168 | 169 |
| 10,000 | 1,229 | 1,218 |
| 10万 | 9,592 | 9,512 |
| 1,000,000 | 78,498 | 78,030 |
| 10,000,000 | 664,579 | 661,459 |
| 1亿 | 5,761,455 | 5,740,304 |
| 1,000,000,000 | 50,847,534 | 50,701,542 |
| 10,000,000,000 | 455,052,511 | 454,011,971 |
| 100,000,000,000 | 4,118,054,813 | 4,110,416,301 |
| 1,000,000,000,000 | 37,607,912,018 | 37,550,193,650 |
| 10,000,000,000,000 | 346,065,536,839 | 345,618,860,221 |
| 100,000,000,000,000 | 3,204,941,750,802 | 3,201,414,635,781 |
| 1,000,000,000,000,000 | 29,844,570,422,669 | 29,816,233,849,001 |
| 10,000,000,000,000,000 | 279,238,341,033,925 | 279,007,258,230,820 |
| 100,000,000,000,000,000 | 2,623,557,157,654,230 | 2,621,647,966,812,030 |
| 1,000,000,000,000,000,000 | 24,739,954,287,740,800 | 24,723,998,785,920,000 |
| 10,000,000,000,000,000,000 | 234,057,667,276,344,000 | 233,922,961,602,470,000 |
| 100,000,000,000,000,000,000 | 2,220,819,602,560,910,000 | 2,219,671,974,013,730,000 |
| 1,000,000,000,000,000,000,000 | 21,127,269,486,018,700,000 | 21,117,412,262,910,000,000 |
| 10,000,000,000,000,000,000,000 | 201,467,286,689,315,000,000 | 201,381,995,844,660,000,000 |
| 100,000,000,000,000,000,000,000 | 1,925,320,391,606,800,000,000 | 1,924,577,459,166,810,000,000 |
| 1,000,000,000,000,000,000,000,000 | 18,435,599,767,349,200,000,000 | 18,429,088,896,563,900,000,000 |
| 10,000,000,000,000,000,000,000,000 | 176,846,309,399,143,000,000,000 | 176,788,931,049,964,000,000,000 |
来源:有多少个素数?在素数页面上。
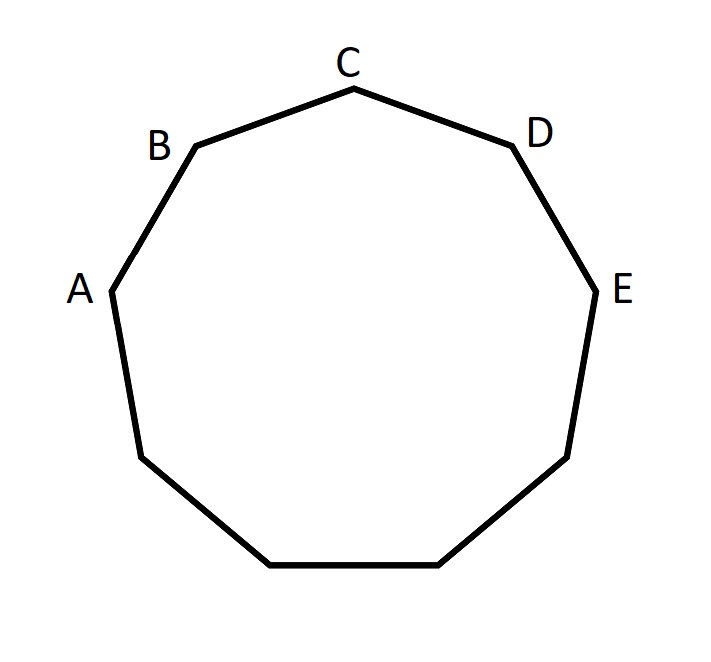
上图是边长为一的九边形。
AB+AC 和 AE 哪个更大?
该问题摘自《门萨公报》2021 年 3 月刊。
以下是我对这个问题的解决方案。(PDF)
假设答案是整数,我怎样才能轻松找到任何三位数或四位数的平方根?
下表显示了数字 0 到 9、每个数字的平方以及该平方的最后一位数字。
平方数的最后一位数字
| 原来的 数字 | 正方形 | 最后一位数字 平方 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 二十五 | 5 |
| 6 | 三十六 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
注意,偶数平方数的尾数总是 0、1、4、5、6 或 9。所有平方数都是如此。这是因为原始数字的最后一位数字决定了平方数的最后一位数字。
步骤1:根据平方数的最后一位数字,我们可以使用下表来缩小平方根的最后一位数字的范围。例如,如果平方数是2809,那么平方根的最后一位数字就是3或7。
原始号码的最后一位
| 最后一位数字 平方根 | 最后一位数字 平方 |
|---|---|
| 0 | 0 |
| 1 | 1 或 9 |
| 4 | 2 或 8 |
| 5 | 5 |
| 6 | 4或6 |
| 9 | 3 或 7 |
步骤2:接下来,取原始数字并删除右边两位数字。例如,如果原始数字是2809,则使用28。
步骤3:找到小于或等于步骤2结果的最小平方数。然后,对该平方数开平方。例如,小于28的最小平方数是25。对25开平方,结果为5。
如果你还没有记住100以内的方块,那么你可以使用下表。
平方根的第一部分
| 第 2 步 | 步骤3 |
|---|---|
| 1 至 3 | 1 |
| 4至8 | 2 |
| 9点到15点 | 3 |
| 16至24岁 | 4 |
| 25至35 | 5 |
| 36至48 | 6 |
| 49至63 | 7 |
| 64至80 | 8 |
| 81至99 | 9 |
步骤 4:如果步骤 1 的结果为 0 或 5,则将其放在步骤 3 的结果之后,就完成了。
否则,令 a = 步骤 3 的结果。令 b=a×(a+1)。例如,如果步骤 3 的结果为 5,则 b=5×6=30。
步骤 5:如果 b < a,则平方根的最后一位数字是步骤 1 中较小者。否则,如果 b >= a,则平方根的最后一位数字是两个可能性中较大者。
步骤 6:要得到平方根,请取步骤 3 的结果,然后将其与步骤 5 的结果相加。换句话说,10×(步骤 3)+步骤 5。
让我们看一些例子:
求 256 的平方根。
- 步骤 1:平方根的最后一位数字是 4 或 6。
- 第 2 步:去掉最后两位数字,得到 2。
- 步骤3:小于或等于2的最小平方是1。1的平方根是1。
- 步骤4:1*(1+1) = 2。
- 步骤 5:步骤 4 的结果等于步骤 2 的结果,因此我们使用步骤 1 中的较大选项作为最后一位数字,即 6。
- 步骤 6:平方根是 3 的结果加上步骤 5 的结果,即 1 & 6 = 16。
求 1369 的平方根。
- 步骤 1:平方根的最后一位数字是 3 或 7。
- 第 2 步:去掉最后两位数字,得到 13。
- 步骤 3:小于或等于 13 的最小平方是 9。9 的平方根是 3。
- 步骤4:3*(1+3) = 12。
- 步骤 5:步骤 2 的结果大于步骤 4 的结果,因此我们使用步骤 1 中较大的选项作为最后一位数字,即 7。
- 步骤 6:平方根是 3 的结果加上步骤 5 的结果,即 3 & 7 = 37。
求 2704 的平方根。
- 步骤 1:平方根的最后一位数字是 2 或 8。
- 第 2 步:去掉最后两位数字,得到 27。
- 步骤 3:小于或等于 27 的最小平方是 25。25 的平方根是 5。
- 步骤4:5*(1+5) = 60。
- 步骤 5:步骤 2 的结果小于步骤 4 的结果,因此我们使用步骤 1 中较小的选项作为最后一位数字,即 2。
- 步骤 6:平方根是 3 的结果加上步骤 5 的结果,即 5 & 2 = 52。
求 5625 的平方根。
- 步骤 1:平方根的最后一位数字是 5。
- 第 2 步:去掉最后两位数字,得到 56。
- 步骤 3:小于或等于 56 的最小平方是 49。49 的平方根是 7。
- 步骤 4:步骤 1 的结果为 0 或 5,因此答案是步骤 3 的结果加上步骤 1 的结果:7 & 5 = 75
求 6561 的平方根。
- 步骤 1:最后一位数字是 1 或 9。
- 第 2 步:去掉最后两位数字,得到 65。
- 步骤 3:小于或等于 65 的最小平方是 64。64 的平方根是 8。
- 步骤4:8*(1+8) = 72。
- 步骤 5:步骤 2 的结果小于步骤 4 的结果,因此我们使用步骤 1 中的较小者作为最后一位数字,即 1。
- 步骤 6:平方根是 3 的结果加上步骤 5 的结果,即 8 & 1 = 81。
您可以在YouTube上看到此方法的演示。
边长为 1 的正五边形的面积是多少?
单击下面的框即可获得答案。
单击下面的框获取提示。
[剧透=提示]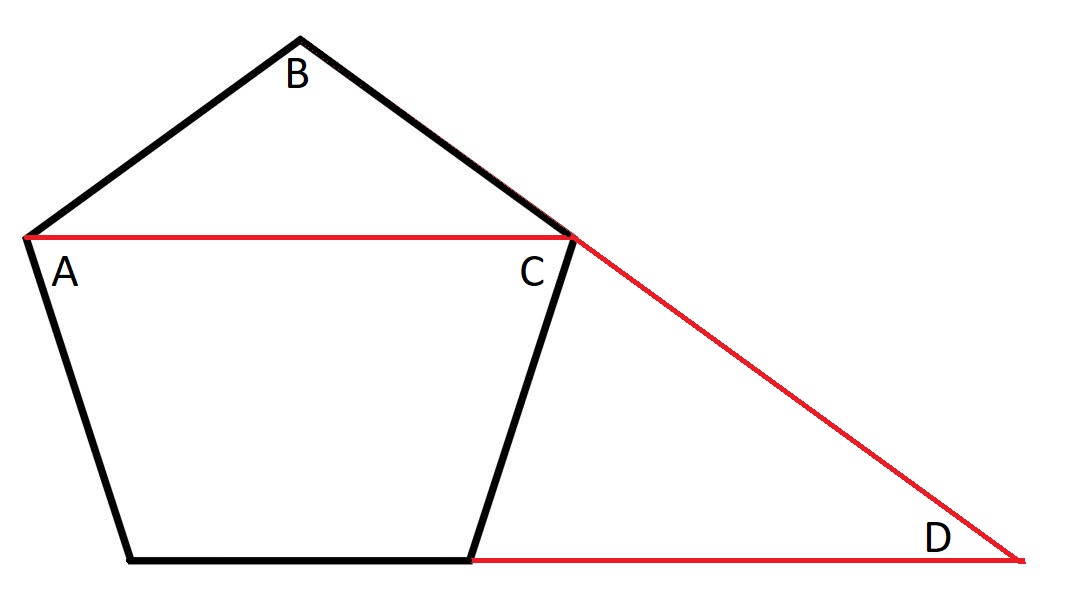
考虑上面的图像。AC = CD。
[/spoiler]这是我的解决方案(PDF)
在一个无风的日子里,查理划着独木舟来到河边,逆流而上。他总是以相同的速度划桨(换句话说,如果我们忽略水流的影响,他的速度总是相同的)。划了一英里后,他的帽子掉进了河里。十分钟后,他意识到帽子不见了,立即掉头顺流追赶。查理在划船的地方追上了帽子。
水流有多快?
以下问题涉及一场酒吧赌注。任何纸币都会随机产生一个美国序列号。玩家从0到9中选择任意三位数字。他必须选择三个不同的数字。获胜取决于这三位数字中有多少位在序列号上至少出现一次。
例如,如果玩家选择 7-0-2,序列号为 22227755,则有两次匹配。2 和 7 多次匹配并不重要。
以下是提供的赔率:
- 3场比赛:5比1
- 2场比赛:1比1
- 1场比赛:9比5
- 0场比赛:15比1
每次下注的获胜概率和庄家优势是多少?
下表显示了每次投注的获胜组合数量、获胜概率以及赌场优势。右列显示赌场优势在 7.4% 到 8.5% 之间。
序列号投注
| 火柴 | 支付 | 组合 | 可能性 | 庄家优势 |
|---|---|---|---|---|
| 3 | 5 | 15,426,684 | 0.154267 | 0.074399 |
| 2 | 1 | 45,771,270 | 0.457713 | 0.084575 |
| 1 | 1.8 | 33,037,245 | 0.330372 | 0.074957 |
| 0 | 15 | 5,764,801 | 0.057648 | 0.077632 |
使用 1 到 9 中的每个数字各恰好一次,组成三个分数,每个分数的分子为一位数,分母为两位数,三个分数之和为一。
例如,8/16 + 9/27 + 3/24 满足所有条件,但总和等于 23/24,而不是 1。
[剧透=解决方案]
有 permut(9,3)*permut(6,3)*permut(3,3)/fact(3) = 60,480 种可能的排列组合需要排序才能找到答案。我必须承认,我反复试验了至少一个小时,却没有找到答案。
因此,我编写了一个程序,对 fact(9) = 362,880 种对这 9 个数字进行排序的方法进行了测试。棘手的部分在于要对这 9 个数字的所有可能排序方式进行排序。以下是使用字典顺序排序的方法。
- 将所有九个元素放入一个数组中,按从低到高的顺序排列。
- 找到数组中最后一个元素,使得下一个元素大于它。如果未找到,则退出程序。
- 从步骤 2 中的下一个元素开始,找到数组中大于步骤 2 中的元素的最后一个元素。
- 交换步骤 2 和步骤 3 中数组中的元素。
- 将数组中的元素从步骤 2 开始依次反转,直到最后。
- 返回步骤 2
按照这个过程,你会找到六次正确答案,一次解决所有六种排序三个分数的方法。[/剧透]
[剧透=代码]
我编写了以下代码,按字典顺序对从 1 到 9 的每个数字进行排序,并测试每个数字是否是解决方案。
无效三分数(无效)
{
int i,x_max,y_max,temp_array[100],保持,pt;
int lex_array[] = { 1,2,3,4,5,6,7,8,9 };
int num_elements = sizeof(lex_array) / sizeof(lex_array[0]);
int 计数 = 0;
bool 停止 = false;
双倍tot3;
cerr << "元素数量 =\t" << num_elements << "\n";
做
{
计数++;
tot3 = (双精度)lex_array[0] / (双精度)(10 * lex_array[1] + lex_array[2]);
tot3 += (双精度)lex_array[3] / (双精度)(10 * lex_array[4] + lex_array[5]);
tot3 += (双精度)lex_array[6] / (双精度)(10 * lex_array[7] + lex_array[8]);
如果 (tot3 == 1.0)
{
cerr << count << "\t";
cerr << lex_array[0] << "/" << lex_array[1] << lex_array[2] << " + ";
cerr << lex_array[3] << "/" << lex_array[4] << lex_array[5] << " + ";
cerr << lex_array[6] << "/" << lex_array[7] << lex_array[8] << "\n";
}
x_max = -1;
对于(i = 0;i <(num_elements - 1);i ++)
{
如果 (lex_array[i] < lex_array[i + 1])
x_max = i;
}
如果(x_max> = 0)
{
y_max = 0;
对于(i = x_max + 1;i < num_elements;i++)
{
如果(lex_array[x_max] < lex_array[i])
y_max = i;
}
保持 = lex_array[x_max];
lex_array[x_max] = lex_array[y_max];
lex_array[y_max] = 保持;
if (x_max + 1 < num_elements - 1) // 反转
{
对于(i = x_max + 1;i < num_elements;i++)
{
temp_array[i] = lex_array[i];
}
pt = 0;
对于(i = x_max + 1;i < num_elements;i++)
{
lex_array[i] = temp_array[num_elements - 1 - pt];
点++;
}
}
}
别的
停止=真;
} 当(停止==假)时;
}
我在Wizard of Vegas论坛上提出并讨论了这个问题。
一位男士有一桶10加仑的酒和一个壶。有一天,他取了一壶酒,然后把酒桶加满水。等酒和水充分混合后,他又取了一壶酒,再次把酒桶加满水。这样,酒桶里的酒和水就等量了。
这个水壶的容量是多少?
[剧透=解决方案]
设 j = 罐子的体积。
第一次装满酒壶后,酒壶中剩余 10 加仑葡萄酒。用水取代葡萄酒后,葡萄酒与整桶葡萄酒的比例为 (10-j)/10。
壶舀出稀释酒后,桶中剩余10焦加仑稀释酒。稀释酒中纯酒的含量可表示为:
(10-j)*((10-j)/10) = 5
(10-j)^2 = 50
j^2 - 20j + 100 = 50
j^2 - 20j + 50 = 0
j = (20 +/- 平方根(400-200))/2
j = (20 +/- 10*sqrt(2))/2
j = 10 +/- 5*sqrt(2)
壶不可能比桶大,所以我们必须使用负号:
j = 10 - 5*sqrt(2) =~ 约 2.92893218813452 加仑。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
为了庆祝感恩节,你和19位数学家围坐在一张圆桌旁。餐桌上的每个人都想吃一份蔓越莓酱,而现在,蔓越莓酱就摆在你面前。
首先,你先自己取。然后,你不再围成一圈传递酱汁,而是随机地把它传给你左边或右边的座位。然后,他们也照做,随机地把它传给他们左边或右边的座位。如此反复,直到每个人都拿到了蔓越莓酱。
圈子里的 20 个人中,谁最有可能最后收到蔓越莓酱?
让我们将其中一位数学家命名为 G。为了使 G 成为最后一位,必须发生两件事:
- 蔓越莓必须首先到达 G 的邻居。
- 蔓越莓必须向相反方向移动 19 个位置,而不能到达 G。
蔓越莓要想成为最后一个,最终必须到达相邻的蔓越莓之一。因此,这种情况发生的概率是 100%。
那么,无论第二部分的概率是多少,对每个人来说都是相同的。因此,每个人排在最后的概率是相等的。
如果这个解释还不够清楚,Gialmere 是从 fivethirtyeight.com 找到这个问题的。他们在这里解释了答案。向下滚动到“上周 Riddler Classic 的答案”部分。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
这是《谜语人》中的另一个谜题。
一个袋子里有100颗弹珠。每颗弹珠要么是红色,要么是蓝色,要么是绿色。如果从袋子里抽出三颗弹珠,那么抽到每种颜色弹珠的概率是20%。请问袋子里每种颜色弹珠的数量是多少?请注意,我并没有明确说明弹珠是随机抽取还是无放回抽取。
让我们尝试在“有放回”的假设下解决这个问题。设 r、b 和 g 分别为红色、蓝色和绿色弹珠的数量。那么,抽到每种颜色弹珠的概率为 6*(r/100)*(b/100)*(g/100)。设该概率等于 0.2,我们可以得出:
6*(r/100)*(b/100)*(g/100) = 0.2
6*r*b*g = 200000
6不能被200,000整除。因此,r*b*g = 33333.333不可能有整数解……所以,我们可以排除替换抽样的情况。
接下来,我们尝试“不重复”假设。在这种情况下,每种颜色各抽取一张的概率是 r*b*g/combin(100,3) = 0.2。试着解一下……
r*b*g/161700 = 0.2
r*b*g = 32340
32340 的质因数分解是 2*2*3*5*7*7*11。
我们需要将这些因子分布在 r、b 和 g 之间,同时保持 r+b+g=100。例如,我们可以尝试:
r = 2*3*5 = 30
b = 2*11 = 22
克=7*7=49
虽然这些正确地用完了所有素数因子,r+b+g = 101,所以它不是一个有效的解决方案。
恐怕我必须编写一个强力循环程序才能以任意顺序获得 r、b 和 g 的值 21、35 和 44 的解决方案。
[/spoiler]以下问题来自Riddler Express 。
让我们假设NFL规则。考虑以下情况:
- 红队在比赛后期落后 14 分
- 红队将有两次机会
- 蓝队将不再拥有任何控球权
- 让我们忽略射门得分和安全分,因为红队必须获得两次达阵才有机会获胜
- 如果比赛进入加时赛,每队获胜的概率均为50%。比赛不能以平局结束。
- 触地得分后踢出一分球的概率为 100%。
- 完成两分转换的概率为 p。
当 p 值为多少时,红队在第一次触地得分(现在落后 8 分)后应该无视踢球并争取两分转换?
设 p = 两分转换和踢球之间的无差异点。
如果第一次两分转换尝试成功,那么红队可以第二次踢球并获胜。
如果第一次两分转换尝试失败,那么红队必须在第二次触地得分后再次尝试,然后在加时赛中赢得比赛。
首次触地得分后,选择两分转换的获胜概率为 p + (1-p)*p/2。我们将其等同于首次触地得分后踢球获胜的概率为 50%,并解出 p。
p + (1-p)*p/2 = 1/2
2p + (1-p)*p = 1
3p-p^2 = 1
p^2 - 3p + 1 = 0
使用二次公式求解 p:
p = (3 +/- 平方根(5))/2
我们采取否定选项,将 p 保持在 0 和 1 之间,得到 p = (3-sqrt(2))/2 = apx。0.381966011250105
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
在之前的“问问巫师”专栏中,有人问过你,连续两次掷两个骰子,达到总点数 12 的预期掷数是多少。顺便提一下,我看到你的论坛上有人声称在掷骰子时目睹了连续 18 次(总共 11 次)的掷骰结果。要达到这个结果,预期掷数是多少?
[spoiler=答案]41660902667961039785742[/剧透]
这是我的解决方案(PDF)。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
借助WizCalc找到了确切的答案。
一片草地呈圆形,半径100米,周围有一道圆形围栏。一只山羊被一条链子拴在围栏上一个固定的钩子上。为了防止山羊长得太胖,农民想确保它只能吃到草地一半的草。链子应该多长?
举例来说,圆圈代表草地。S 代表链条在草地边缘的位置。圆圈的黄色部分是山羊可以到达的地方。绿色区域是链条无法到达的地方。目标是让链条的距离合适,使绿色和黄色部分相等。
请参考下图来解决这个问题。
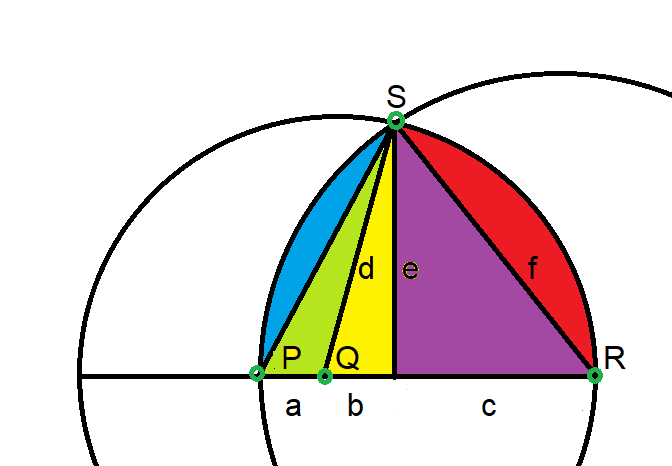
点 Q 是草圈的中心。山羊的链条固定在点 R。山羊可以到达所有彩色区域,包括 PR 线以下的镜像区域。
已知草地圆的半径为 100,因此 b+c = d = 100。
我解决这个问题的方法是,用 b 来定义一切。然后我会调整 b 的值,直到达到预期的效果,也就是山羊可以吃掉一半的草。
我们先来求解 e 中 b 的项。观察边长为 b、d 和 e 的三角形,并运用勾股定理:
b^2 + e^2 = d^2
b^2 + e^2 = 10000
e = 平方根(10000 - b^2)
接下来,我们用 b 来求解 f。记住,我们已经知道 b+c=100,所以 c=100-b。运用勾股定理:
c^2 + e^2 = f^2
(100-b)^2 + (10000 - b^2) = f^2
f^2 = 10000 - 200b + b^2 + 10000 - b^2
f^2 = 20000 - 200b
f^2 = 100*(200 - 2b)
f = 10*sqrt(200-2b)
接下来,我们来求三角形 QRS 的面积:
QRS = (1/2)*100*e = 50*sqrt(10000 - b^2)
接下来,让我们求出由角度 SQR 切出的草地切片的面积:
tan(SQR) = e/b = sqrt(10000-b^2)/b。
切片 SQR = atan(sqrt(10000-b^2)/b)
红色区域等于切片 SQR 减去三角形 QRS = 5000*atan(sqrt(10000-b^2)/b) - (1/2)*100*e = 50*sqrt(10000 - b^2)。
接下来,我们来找出蓝色 + 绿色 + 黄色 + 紫色的区域。为此,我们需要找到 QRS 角。
tan(QRS) = e/c = sqrt(10000-b^2)/(100-b)
角度 QRS = atan(sqrt(10000-b^2)/(100-b))。
加上红色区域,我们就得到了山羊可以吃的总面积的一半:
atan(sqrt(10000-b^2)/(100-b)) + 50*sqrt(10000 - b^2)。
将其加倍,即可得到 PR 线下方部分的总面积:
2*atan(sqrt(10000-b^2)/(100-b)) + 100*sqrt(10000 - b^2)。
草地总面积为10,000*pi。
现在,只需调整 b 的值,直到得到山羊可以吃掉的面积等于 5,000*pi 的值。Excel 中的 goalseek 函数非常适合解决这类问题。我不知道在电子表格出现之前人们是如何完成任何事情的。
使用此方法,您会发现b = 32.867402。
从那里我们可以得到 f = 链的长度 = 115.8728598 米。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
为了回答这个问题,我首先根据允许的 Wordle 解决方案列表查看了每个字母在每个位置出现的频率。
Wordle 中的字母频率
| 信 | 位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 全部的 |
|---|---|---|---|---|---|---|
| 一个 | 141 | 304 | 307 | 163 | 64 | 979 |
| B | 173 | 16 | 57 | 24 | 11 | 281 |
| C | 198 | 40 | 56 | 152 | 31 | 477 |
| D | 111 | 20 | 75 | 69 | 118 | 393 |
| 埃 | 72 | 242 | 177 | 318 | 424 | 1233 |
| F | 136 | 8 | 二十五 | 三十五 | 二十六 | 230 |
| 格 | 115 | 12 | 67 | 76 | 41 | 311 |
| 哈 | 69 | 144 | 9 | 二十八 | 139 | 389 |
| 我 | 三十四 | 202 | 266 | 158 | 11 | 671 |
| J | 20 | 2 | 3 | 2 | 0 | 二十七 |
| 钾 | 20 | 10 | 12 | 55 | 113 | 210 |
| 左 | 88 | 201 | 112 | 162 | 156 | 719 |
| 米 | 107 | 三十八 | 61 | 68 | 四十二 | 316 |
| 否 | 三十七 | 87 | 139 | 182 | 130 | 575 |
| 哦 | 41 | 279 | 244 | 132 | 58 | 754 |
| 磷 | 142 | 61 | 58 | 50 | 56 | 367 |
| 问 | 23 | 5 | 1 | 0 | 0 | 二十九 |
| R | 105 | 267 | 163 | 152 | 212 | 899 |
| 秒 | 366 | 16 | 80 | 171 | 三十六 | 669 |
| T | 149 | 77 | 111 | 139 | 253 | 729 |
| ü | 33 | 186 | 165 | 82 | 1 | 467 |
| 五 | 43 | 15 | 49 | 46 | 0 | 153 |
| 西 | 83 | 四十四 | 二十六 | 二十五 | 17 | 195 |
| 十 | 0 | 14 | 12 | 3 | 8 | 三十七 |
| 是 | 6 | 23 | 二十九 | 3 | 364 | 425 |
| Z | 3 | 2 | 11 | 20 | 4 | 40 |
然后,我查看了Wordle答案列表中所有包含五个不同字母的单词,并根据上面的字母频率表对它们进行评分。正确位置的匹配得两分,错误位置的匹配得一分。然后,我对列表进行了排序,如下所示。
Wordle 中的最佳起始词
<!--/框标题-->| 秩 | 单词 | 居中">点|
|---|---|---|
| 1 | 盯 | 5835 |
| 2 | 出现了 | 5781 |
| 3 | 石板 | 5766 |
| 4 | 增加 | 5721 |
| 5 | 出现 | 5720 |
| 6 | 更理智 | 5694 |
| 7 | 圈套 | 5691 |
| 8 | 愤怒 | 5682 |
| 9 | 陈旧 | 5665 |
| 10 | 箱 | 5652 |
| 11 | 痕迹 | 5616 |
| 12 | 之后 | 5592 |
| 十三 | 分享 | 5562 |
| 14 | 店铺 | 5547 |
| 15 | 吓 | 5546 |
| 16 | 改变 | 5542 |
| 17 | 起重机 | 5541 |
| 18 | 警报 | 5483 |
| 19 | 泪流满面 | 5479 |
| 20 | 炒 | 5475 |
| 21 | 迎合 | 5460 |
| 22 | 空闲的 | 5457 |
| 23 | 独自的 | 5452 |
| 24 | 贸易 | 5449 |
| 二十五 | 鼾 | 5403 |
| 二十六 | 篦 | 5403 |
| 二十七 | 页岩 | 5392 |
| 二十八 | 至少 | 5390 |
| 二十九 | 披肩 | 5377 |
| 三十 | 规模 | 5376 |
| 31 | 反应 | 5376 |
| 三十二 | 布莱尔 | 5368 |
| 33 | 解析 | 5351 |
| 三十四 | 强光 | 5340 |
| 三十五 | 赎罪 | 5338 |
| 三十六 | 学习 | 5324 |
| 三十七 | 早期的 | 5320 |
| 三十八 | 倾斜 | 5307 |
| 三十九 | 帕勒 | 5285 |
| 40 | 耀斑 | 5280 |
| 41 | 走道 | 5280 |
| 四十二 | 支撑 | 5274 |
| 43 | 偷 | 5268 |
| 四十四 | 瞬间 | 5267 |
| 45 | 分数 | 5258 |
| 46 | 清除 | 5258 |
| 四十七 | 老妪 | 5253 |
| 四十八 | 石头 | 5253 |
| 49 | 心 | 5252 |
| 50 | 失败者 | 5251 |
| 51 | 锥度 | 5248 |
| 52 | 仇恨者 | 5243 |
| 53 | 中继 | 5241 |
| 54 | 盘子 | 5240 |
| 55 | 崇拜 | 5239 |
| 56 | 酱 | 5236 |
| 57 | 更安全 | 5235 |
| 58 | 外星人 | 5233 |
| 59 | 种姓 | 5232 |
| 60 | 剪切 | 5231 |
| 61 | 巴莱尔 | 5230 |
| 62 | 警笛 | 5226 |
| 63 | 独木舟 | 5215 |
| 64 | 郡 | 5213 |
| 65 | 肾脏 | 5210 |
| 66 | 层 | 5206 |
| 67 | 驯兽师 | 5200 |
| 68 | 大的 | 5196 |
| 69 | 珍珠 | 5196 |
| 70 | 路线 | 5194 |
| 71 | 支撑 | 5192 |
| 72 | 片 | 5178 |
| 73 | 阶段 | 5171 |
| 74 | 散文 | 5170 |
| 75 | 孢子 | 5169 |
| 76 | 唤醒 | 5166 |
| 77 | 优雅 | 5164 |
| 78 | 太阳的 | 5152 |
| 79 | 套房 | 5150 |
| 80 | 烤 | 5145 |
| 81 | 拉格啤酒 | 5130 |
| 82 | 飞机 | 5129 |
| 83 | 夹板 | 5129 |
| 84 | 已处理 | 5128 |
| 85 | 矛 | 5126 |
| 86 | 伟大的 | 5126 |
| 87 | 艾德 | 5123 |
| 88 | 比喻 | 5116 |
| 89 | 尖塔 | 5108 |
| 90 | 踏 | 5107 |
| 91 | 奴隶 | 5097 |
| 92 | 关闭 | 5090 |
| 93 | 槊 | 5090 |
| 94 | 冲洗 | 5088 |
| 95 | 原因 | 5087 |
| 96 | 易于 | 5087 |
| 97 | 无人机 | 5082 |
| 98 | 噪音 | 5079 |
| 99 | 波峰 | 5073 |
| 100 | 清醒 | 5068 |
所以,我推荐的起始词,也就是我使用的词,是STARE。
i^i 是什么
这是我的解决方案(PDF)。
你想玩一个需要两枚普通六面骰子的游戏。很遗憾,你丢了骰子。不过,你有九张索引卡,你可以随意标记。玩家必须从九张索引卡中随机选择两张,不能重复,然后计算两张卡的点数之和。
按如下方式标记卡片:
1 @ 0.5
1 @ 1.5
2 @ 2.5
1 @ 3.5
2 @ 4.5
1 @ 5.5
1 @ 6.5
我在Wizard of Vegas论坛上提出并讨论了这个问题。
抛一枚公平的硬币,最终落在最初朝上的一面的可能性更大,这是真的吗?
证据表明这是真的!
斯坦福大学的佩尔西·迪亚科尼斯和苏珊·霍姆斯记录了10000次抛硬币实验。硬币落地时正面朝上的概率为50.8%(来源:美国数学学会期刊《数学科学动态》中的 “51%解决方案”)。出现如此高或更高比例的概率为5.48%。
为了从数学上证明这一点,我假设硬币的实际旋转次数服从泊松分布。更具体地说,如果平均旋转次数为m,那么恰好旋转n次的概率为exp(-m)*m^n/n!。为了说明泊松分布,下图显示了假设平均值为10,硬币旋转0到25次的概率。
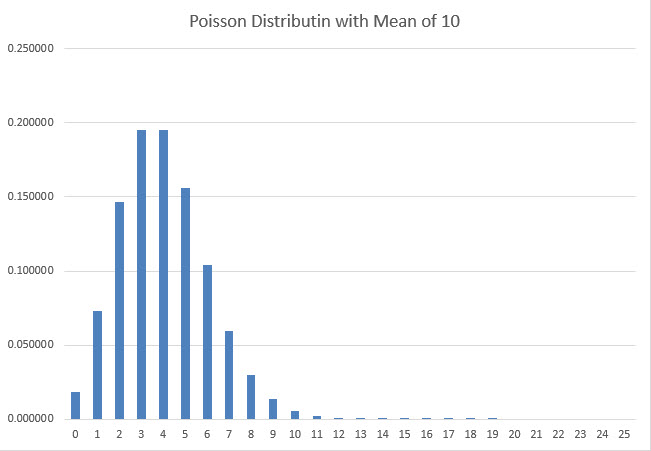
我选择泊松假设的原因是,当均值足够大时,它遵循近似钟形曲线的形状,并且实际结果永远不会低于零。
然后,我计算了不同半转均值下,半转次数为偶数(最终落地时与起始位置同一侧朝上)的概率。下表显示了均值在0.5到5.0之间的结果。
旋转次数为偶数和奇数的概率
| 平均革命 | 偶数总计 | 奇数总数 |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
我开始好奇,为什么偶数的概率总是大于 50%。事实证明,给定平均值 m,偶数的概率可以表示为 0.5 + e^(-2m)/2。e 的任意次方必定为正数,因此旋转次数为偶数的概率也为正数。
您可以在此处看到我对该公式的证明。
解出 x:
9x + 12x = 16x
[spoiler=答案]=(log(1+SQRT(5))-log(2))/(log(4)-log(3)) =~ 1.67272093446233。[/剧透]
这是我的解决方案(PDF)。
我在Wizard of Odds论坛上提出并讨论了这个问题。
这个问题的灵感来自于视频《一个困难的指数问题》 。
你的办公室有100名员工,他们会举行一个秘密圣诞礼物交换活动。你会把每个人的名字写在一张纸上,然后把纸放进一顶帽子里,然后每个人随机抽取一个名字作为礼物送给他们。
问题是,平均会有多少个闭环?
大小为 4 的闭环示例:Gordon 给 Don,Don 给 Jon,Jon 给 Nathan,Nathan 给 Gordon。
画出自己的名字将是一个大小为 1 的闭环。
[剧透=解决方案]
假设只有一名员工参加秘密圣诞派对。显然他会自己挑选,这样就形成了一个闭环。
然后,第二个员工迟到了,请求加入。他们给了她一份现在两名员工的名单。她选择员工 1 的概率是一半,而自己选择员工 2 的概率是一半。如果她选择了员工 1,那么她就可以挤进员工 1 的循环中,她为员工 1 买东西,员工 1 也为她买东西。所以,现在的概率是 1 + 0.5*1 = 1.5
然后,第三个员工迟到了,要求加入。他们给了她一份现在有3名员工的名单。她选择员工1或2的概率是2/3,而自己选择员工1或2的概率是1/3。如果她选择了员工1或2,那么她就可以被挤进他们的循环中,她会为她选择的员工买单,而原本应该为该员工买单的人现在要为3号员工买单。所以,现在的概率是1.5 + (1/3) = 11/6。
然后,第四位员工迟到了,要求加入。店员给了她一份现在有四名员工的名单。她选择员工 1 到 3 的概率是 3/4,而自己选择员工 1 到 3 的概率是 1/4。如果她选择了员工 1 到 3,那么她就可以被挤进他们的循环中,她会为她选择的员工买单,而原本应该为该员工买单的人现在要为 4 买单。所以,现在的概率是 11/6 + (1/4) = 25/12。
继续这样做,最终答案是 1/1 + 1/2 + 1/3 + ... + 1/100 =~ 5.187377518。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
考虑一个半径为 1 的半圆,里面有两个堆叠的矩形。这两个矩形的最大合并面积是多少?
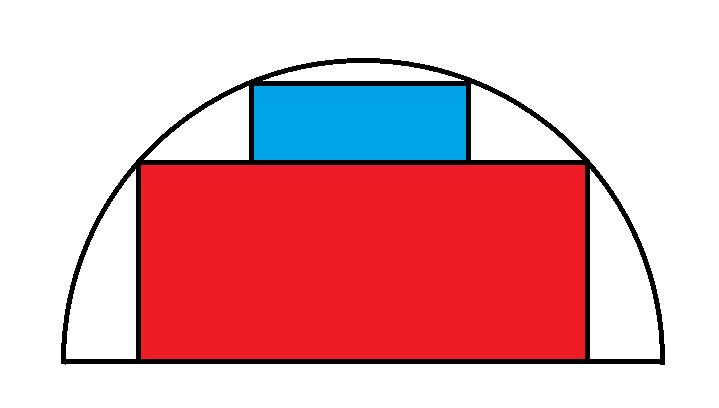
请忽略同卵双胞胎,假设每个孩子出生时男孩或女孩的概率均为50%。如果从2到5人的家庭中随机抽取孩子,那么男孩或女孩有姐妹的概率是多少?
有趣的是,无论家庭规模如何,无论性别如何,概率都是相同的。
以三口之家为例。以下是八种可能的男孩和女孩的排列顺序:
血脑屏障
BBG
英国国立卫生研究院
布格
GBB
GBG
黄金海岸
GG
如果你从上面的列表中随机挑选一个女孩,你会发现12个女孩中有9个有姐妹。12个男孩也是如此,9个有姐妹。所以,概率是9/12 = 3/4。
当孩子数量为 n 时,任何孩子有姐妹的概率的一般公式是 1-(1/2) n-1 。
以下是家庭中孩子总数中有一个姐妹的概率:
- 1:0
- 2:1/2
- 3:3/4
- 4:7/8
- 5:15/16
- 6:31/32
或者说,男孩和女孩的概率相同也是合理的。兄弟姐妹的性别与你的性别无关。因此,只有家庭规模才重要,而不是你自己的性别。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
首先,让我们制作一个合适的图表并标注它。
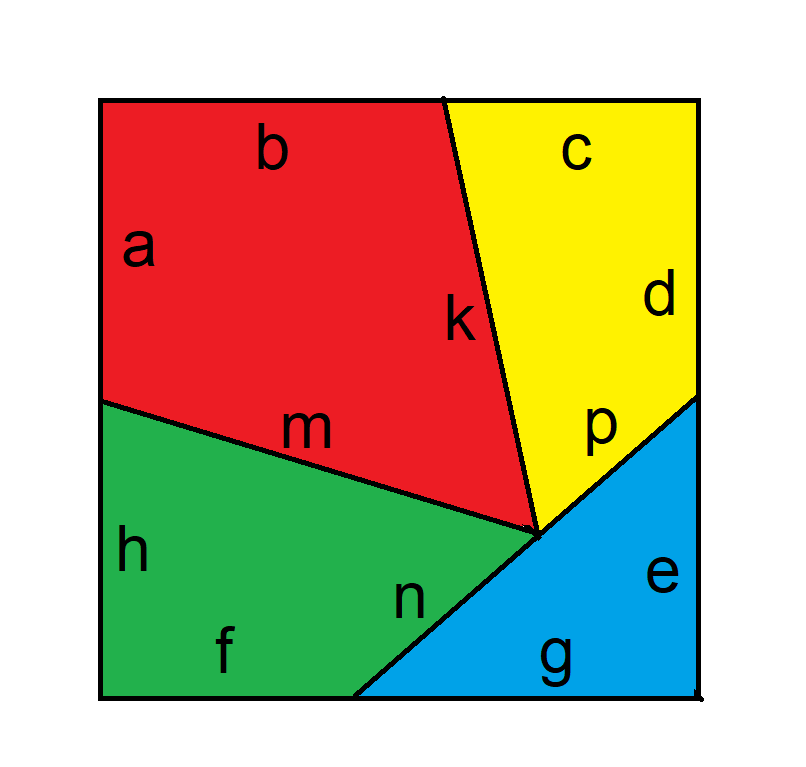
以下只是已解三角形的图。
[剧透=已解三角形]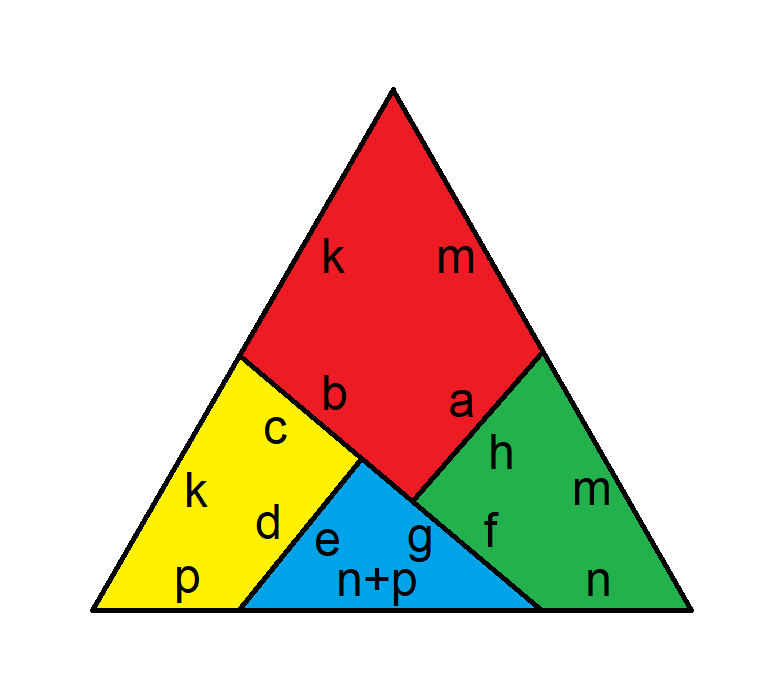 [/spoiler]
[/spoiler]接下来,假设正方形的边长为 1,这里只是上图中每个字母的长度。
[/spoiler]a = d = e = h = 1/2
b = g = SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0.572145321740575
c = f = 1-SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0.427854678259425
k = m = 1/SQRT(SQRT(3)) =~ 0.759835685651592
n = (3-SQRT(4*SQRT(3)-3))/(2*SQRT(SQRT(3))) =~ 0.386767938902275
p = (SQRT(4*SQRT(3)-3)-1)/(2*SQRT(SQRT(3))) =~ 0.373067746749317
[/spoiler]最后,这是我的完整解决方案(PDF)。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
我相信你是《生活大爆炸》的粉丝。我最喜欢的场景之一是“石头剪刀布蜥蜴史波克”的游戏。它就像一个五格石头剪刀布的游戏,规则如下:
- 纸包石头
- 岩石压碎蜥蜴
- 蜥蜴毒害了斯波克
- 斯波克砸碎剪刀
- 剪刀剪纸
- 蜥蜴吃纸 斯波克蒸发岩石
- 剪刀斩首蜥蜴
- 论文反驳了斯波克
- 石头压碎剪刀
我的问题是是否可以添加更多符号,以便每一方对抗随机玩家都有相同的机会?
是的,我也很喜欢那个场景!这里有一个YouTube视频。
你需要奇数个符号。理论上,你可以有偶数个符号,但这样你就必须制定规则,规定某些不同的符号组合会导致平局。不,我们想要一个决定性的游戏,只有当两个玩家都打出相同的符号时才会平局。
用素数符号来解释,会显得尤为优雅和容易。请允许我以七个符号为例进行说明。我们将符号标记为 A 到 G,并在下图中将它们表示在一个圆圈上。
接下来,从 A 开始,然后顺时针画一个箭头指向下一个符号。箭头应指向这两个符号之间的那个点。想象一下,这个符号被一支箭射中了。继续顺时针画,直到回到 A。图表不会像这样:
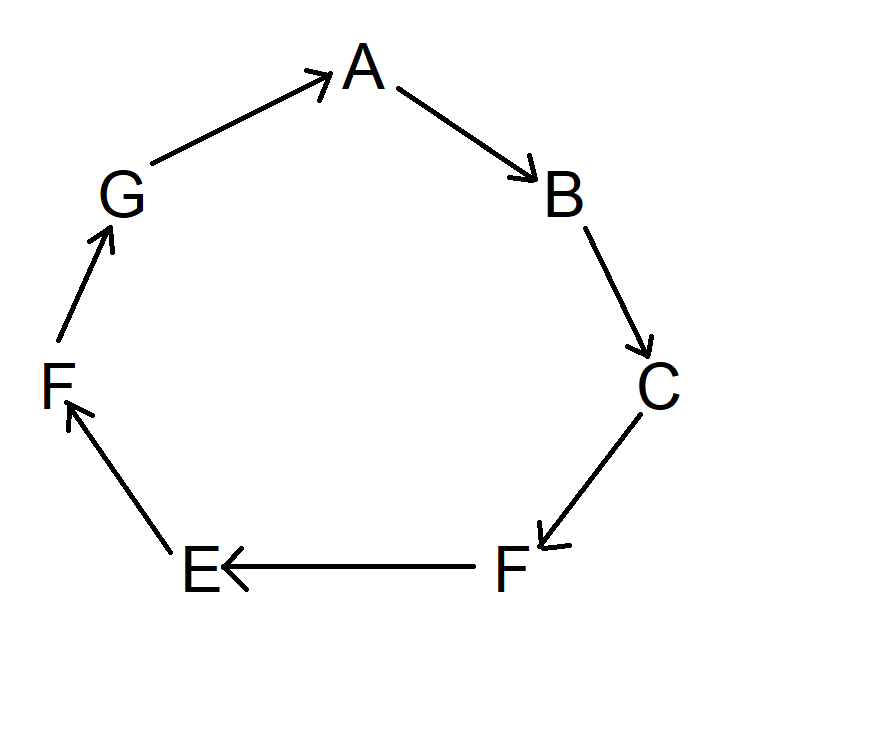
接下来,重复同样的步骤,但从 A 点开始,顺时针移动两个符号。实际上,你可以从任意位置开始。现在的图表如下:
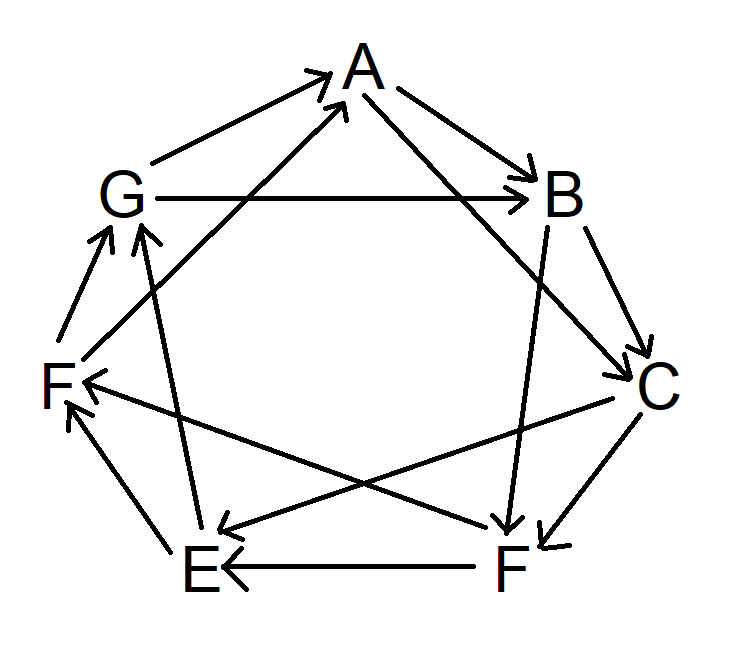
最后,重复同样的步骤,但要顺时针跳过三个符号。图表现在看起来如下:
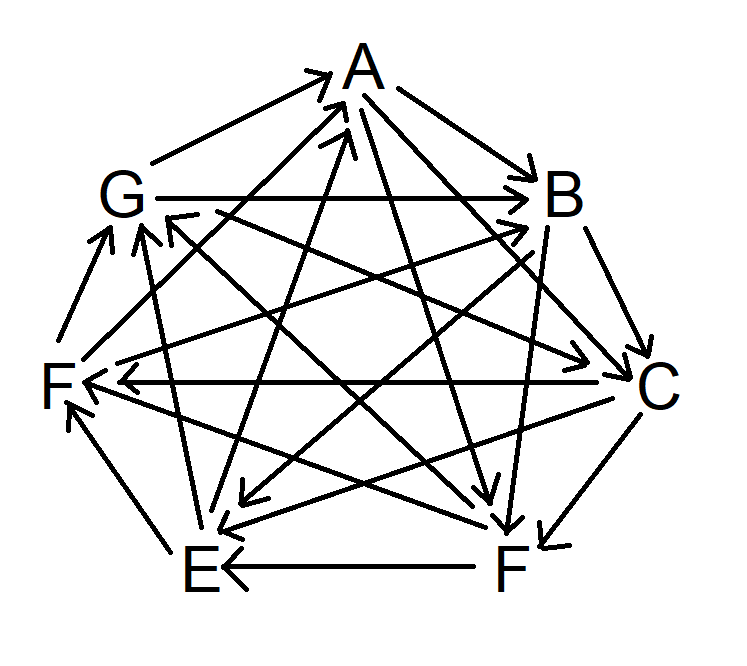
请注意,此时每个符号都击败其他三个符号,并且被其他三个不同的符号击败。
这种方法适用于任何素数个符号,因为当你回到原始符号时,你已经遍历了所有符号。对于 n 个符号,你需要重复这个过程 (n-1)/2 次。
你可以用任意奇数个符号来打造平衡的游戏,但有时你会很快回到原始符号。当这种情况发生时,你必须从错过的符号开始进行其他循环。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
你洗好一副标准(28张)多米诺骨牌,然后随机抽取一张。你小心地翻开其中一面,发现是一张6。这张牌是双6的概率是多少?
为了方便那些不熟悉多米诺骨牌的人理解,一张多米诺骨牌有两面,每面都有一个从0到6的数字。一组多米诺骨牌由每种可能的多米诺骨牌各一张组成。这意味着所有 combin(7,2)=21 种方法可以从 7 个数字中选择数字,无需替换,再加上所有 7 种方法,使两个数字都在同一面。
全部 28 个如下:0-0、0-1、0-2、0-3、0-4、0-5、0-6、1-1、1-2、1-3、1-4、1-5、1-6、2-2-2、2-3、2-4、2-5、2-6、3-3、3-4、3-5、3-6、4-4、4-5、4-6、5-5、5-6、6-6。
解释清楚之后,下面就是答案和解决方案。
换个简单的说法,这个问题就是:随机抽取一张多米诺骨牌,两面数字相同的概率是多少?答案很简单,就是 7/28 = 1/4。
你可能会说,答案应该是 1/7,因为另一面可能是七个可能数字中的任意一个。没错,它可能是七个数字中的任意一个,但它们出现的概率并不相等。6-6 多米诺骨牌应该重复计算,因为它有两面,每面都有一个六。所以,另一面可能是两个六中的任何一个,而这组牌一共有八个六。因此,答案是 2/8 = 1/4。
这个问题是我在“拉斯维加斯巫师”论坛上提出并讨论的。谨以此问题纪念艾伦·门德尔森。
艾伦和鲍勃决定打网球,直到其中一人连续赢两局。艾伦赢得任何一局的概率是2/3。那么艾伦赢得比赛的概率是多少?
艾伦和鲍勃决定打网球,直到其中一人连续赢两局。艾伦赢得任何一局的概率是2/3。那么艾伦赢得比赛的概率是多少?
以下是艾伦赢得单场比赛的任何概率的生成解决方案。
设 p = a 获胜的概率。
令 a = 艾伦赢得上一场比赛后赢得锦标赛的概率。
令 b = 鲍勃赢得最后一场比赛后艾伦赢得锦标赛的概率。
(1)a = p + (1-p)*b
(2)b = p*a
将方程(2)代入方程(1)中:
a = p + (1-p)*pa
a = p + pa - p 2 *a
a - pa + p 2 *a = p
a(1-p+ p2 )=p
(3)a = p/(1-p + p 2 )
将方程(3)代入方程(2)中:
b = p 2 /(1-p + p 2 )
第一场比赛将决定赢得比赛的概率是 a 还是 b:
答案 = pa + (1-p)b
= p 2 /(1-p+p 2 ) + (1-p)*p 2 /(1-p+p 2 )
= (2a 2 -a 3 )/(a 2 -a+1)
设 a=2/3,则赢得比赛的概率为 16/21。
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
你有一架5英尺高的梯子。你想把它靠在墙上,尽可能高。但是,你必须把梯子放在一个1x1x1立方英尺的箱子上。不行,你不能移动这个箱子。梯子顶部能达到的最大高度是多少?
这是我的解决方案(PDF)。
x 1/x在什么值时达到最大值?
答案是 e =~ 2.71828182845905。
其中,e^(1/e) 的值 =~ 1.44466786100977。
这是我的解决方案(PDF)。
1944 年的报纸注意到了这个令人难以置信的巧合:
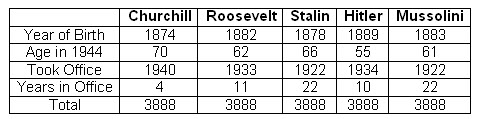
这是一个巨大的巧合还是其中存在某种数学技巧?
这是一个数学技巧,也是一个已知魔术的基础。
对于所有在 1944 年还活着的人来说,他们的年龄(生日后)加上出生年份,就是 1944 年。想想看。如果你当时 x 岁,那么你出生于 1944-x 年。总和是 x + (1944-x) = 1944 年。
这与 1944 年的“任职年限”是一样的。如果您任职 y 年,那么您一定是在 1944-y 年开始任职的。y + (1944-y) = 1944。
1944 + 1944 的总和 = 3,888。每次都有效。
为了将其变成一个在 2023 年有效的魔术,我们需要将以下四件事相加:
- 出生年份
- 他们今年几岁了?
- 发生某些重大事件的年份(例如第一个孩子的出生)。
- 今年是这一重大事件的周年纪念日。
它的总和始终为 2023 + 2023 = 4046。
我在Wizard of Vegas论坛上提出并讨论了这个问题。