请问巫师 #426
假设一个序列号从 1 开始按顺序编号。流通中的序列号最大值未知。给定 n 个随机抽样,最大序列号的最佳估计值是多少?
我喜欢用计算序列号平均间距的方式来解答这个问题。计算方法是用最大值除以样本容量。例如,如果样本中最大的序列号是 1000,样本容量为 5,那么平均间距就是 1000/5=200。然后把这个平均间距加到最大序列号上,就能得到估计的最大序列号。在这个例子中,1000+200=1200。
通常的计算公式是 M*(k+1)/k,其中 M 为最大值,k 为观测次数。在本例中,该公式得出 1000*(6/5) = 1200。
如图所示,ABCD 是一个边长为 10 的正方形。在其内部分别内切了一个半圆和一个四分之一圆。
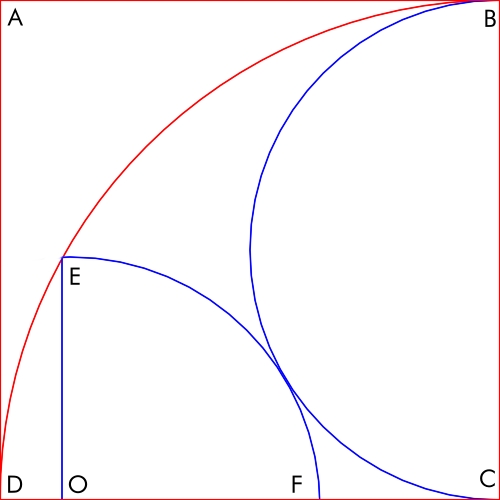
OE的长度是多少?
请参考下图。
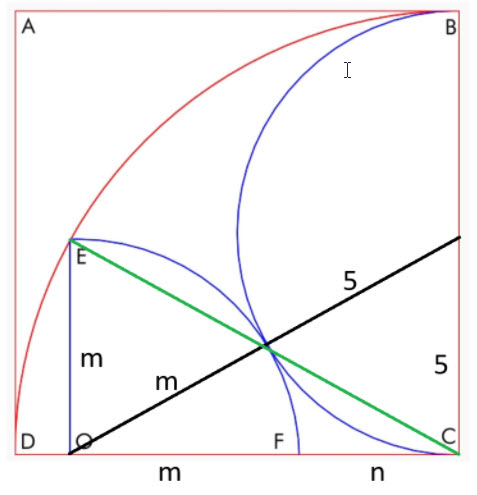
这里有两个直角三角形,一个斜边为绿色,另一个斜边为黑色。我们来列出这两个三角形的勾股定理方程:
- 绿色斜边: m² + (m+n) ² = 10²
- 黑边斜边: 5² + (m+n) ² = (m+5) ²
让我们将第一个方程重新整理为 (m+n) 2 = 10 2 - m 2
让我们把 (m+n) 2的值代入第二个方程:
5² + 10² - m² = (m+5) ²
25 + 100 - m 2 = m 2 + 10m + 25
2m² + 10m - 100 = 0
m² + 5m - 50 = 0
利用勾股定理求解 m:
m = (-5 +/- sqrt(25 + 200))/2
m = 5 或 -10。5 是唯一合理的答案。
[剧透结束]这个问题在我的Wizard of Vegas论坛上被提出和讨论过。
大量学生参加一个包含 10 道题的测试。每道题都是判断题。最多有多少学生参加测试,才能保证任意两份试卷的题目至少不同两道?
选取其中一项测试作为我们称之为关键测试的测试。
第 1 组 = 其他测试与关键测试恰好相差 2 道题的方法数为 combin(10,2)=45。
我不会计算与关键测试结果相差 3 的方法数,因为其中一些方法与第 1 组的测试结果有 9/10 的匹配度。
第二组 = 其他测试与关键测试恰好相差 4 道题的方法数为 combin(10,4)=210。这些测试中的任何一个都至少与第一组中的任何测试相差 2 道题。
重复这个逻辑……
- 第 3 组 = 其他测试与关键测试恰好有 6 道题不同的方法数为 combin(10,6)=210。
- 第 4 组 = 其他测试与关键测试恰好相差 8 道题的方法数为 combin(10,8)=45。
- 第 5 组 = 其他测试与关键测试恰好相差 10 道题的方法数为 combin(10,10)=1。
所以,答案是第 1 组到第 5 组的总和加上关键测试的 1 = 1+45+210+210+45+1 = 512。
这个数字和 2 的 9 次方一样。这会是巧合吗?不!
从一组较大的物品中抽取奇数个物品的方法数与抽取偶数个物品的方法数相同。这是因为大组中的每个物品都可以被选中或不被选中。对于包含 n 个物品的组,每个物品被选中或不被选中共有 2^n 种组合。如果按二进制顺序系统地列出这些组合,则奇数和偶数的组合数会交替出现。由于该组的总数为 2^n,而 2^n 本身是偶数,因此 2^n 的一半是偶数。
因此,第 1 组到第 5 组题目的数量之和,就是选择偶数个与关键测试题匹配的题目的方法数。这等于选择奇数个与关键测试题匹配的题目的方法数。与关键测试题匹配或不匹配的总方法数为 2^10 = 1024。其中一半的题目匹配偶数次。所以,答案是 1024/2 = 512。
这个问题在我的Wizard of Vegas论坛上被提出和讨论过。


