请问巫师 #422
为了便于讨论,假设一个二十一点游戏有无限多副牌,允许无限次重新分牌,并且玩家可以分任何一对牌。那么,玩家最终打出任意给定数量的牌的概率是多少?
重新分牌为 n 手的概率为 (combin(2*(n-1),n-1)/n) × (1/13)^(n-1) × (12/13)^n 。关于第一项的更多信息(我需要一些帮助),请查阅Catalan numbers 。
下表显示了最终牌型为1到20的概率。秒数列表示“树”的数量,也就是上述表达式中的卡泰罗尼亚数。
| 手 | 树木 | 可能性 |
|---|---|---|
| 1 | 1 | 0.9230769230769 |
| 2 | 1 | 0.0655439235321 |
| 3 | 2 | 0.0093080128093 |
| 4 | 5 | 0.0016523099661 |
| 5 | 14 | 0.0003285065968 |
| 6 | 四十二 | 0.0000699777366 |
| 7 | 132 | 0.0000156163334 |
| 8 | 429 | 0.0000036037693 |
| 9 | 1430 | 0.0000008529631 |
| 10 | 4862 | 0.0000002059225 |
| 11 | 16796 | 0.0000000505114 |
| 12 | 58786 | 0.0000000125531 |
| 十三 | 208012 | 0.0000000031540 |
| 14 | 742900 | 0.0000000007998 |
| 15 | 2674440 | 0.0000000002045 |
| 16 | 9694845 | 0.0000000000526 |
| 17 | 35357670 | 0.0000000000136 |
| 18 | 129644790 | 0.0000000000035 |
| 19 | 477638700 | 0.00000000000009 |
| 20 | 1767263190 | 0.0000000000002 |
我听说毕达哥拉斯三元组有无数个。有什么公式可以求出它们吗?
是的,有无数个独特的毕达哥拉斯三元组!对于那些不熟悉这个术语的人来说,它们是直角三角形,每条边都是整数。3-4-5 是最著名的一个。为了得到一个独特的(换句话说,不可约的)集合,毕达哥拉斯三元组可以为 a 和 b 选择任意整数值,其中 a < b,并且一个为奇数,一个为偶数。
- 第 1 条腿 = b 2 - a 2
- 第 2 条腿 = 2ab
- 斜边 = a 2 + b 2
下表列出了所有边长均为 101 或更小的不可约勾股数。
| a,b | 第 1 站 | 第 2 站 | 斜边 |
|---|---|---|---|
| 1,2 | 3 | 4 | 5 |
| 1,4 | 8 | 15 | 17 |
| 1,6 | 12 | 三十五 | 三十七 |
| 1,8 | 16 | 63 | 65 |
| 1,10 | 20 | 99 | 101 |
| 2,3 | 5 | 12 | 十三 |
| 2.5 | 20 | 21 | 二十九 |
| 2,7 | 二十八 | 45 | 53 |
| 2,9 | 三十六 | 77 | 85 |
| 3,4 | 7 | 24 | 二十五 |
| 3,6 | 二十七 | 三十六 | 45 |
| 3,8 | 四十八 | 55 | 73 |
| 4,5 | 9 | 40 | 41 |
| 4,7 | 33 | 56 | 65 |
| 4,9 | 65 | 72 | 97 |
| 5,6 | 11 | 60 | 61 |
| 5,8 | 三十九 | 80 | 89 |
| 6,7 | 十三 | 84 | 85 |
使用两个骰子,在掷出七点之前,至少掷出两次除七点之外的其他所有点数的概率是多少?
这类问题的诀窍在于,如果掷骰子之间的时间遵循平均值为 1 的指数分布,则概率相同。在这种情况下,可以用以下公式给出。
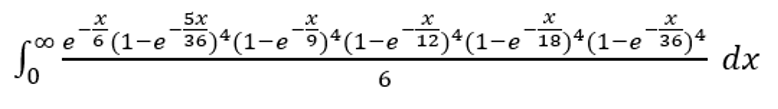
以文本形式表示:exp(-x/6)*(1-exp(-5x/36))^4*(1-exp(-4x/36))^4*(1-exp(-3x/36))^4*(1-exp(-2x/36))^4*(1-exp(-1x/36))^4/6
为了解决此类积分,我推荐使用这个积分计算器。
答案是 7864581698887803455719/10946915593544650625105200 =~ 0.0007184290069364848。


