请问巫师 #367
我喜欢在掷骰子游戏中押注所有数字。在掷出7之前,我预计会击中多少个不同的数字?
为了其他读者的利益,问题是询问在掷出总数七之前,两次掷骰子会掷出以下多少个总数:4、5、6、8、9 和 10。
答案是 2.375758。下表显示了在指定范围内掷出 0 到 6 个不同点数的概率。右下角单元格显示的是掷出 7 点之前的平均不同点数。
滚动的唯一数字
| 全部的 | 可能性 | 预期的 |
|---|---|---|
| 6 | 0.062168 | 0.373009 |
| 5 | 0.101016 | 0.505079 |
| 4 | 0.129245 | 0.516979 |
| 3 | 0.151531 | 0.454594 |
| 2 | 0.170057 | 0.340114 |
| 1 | 0.185983 | 0.185983 |
| 0 | 0.200000 | 0.000000 |
| 全部的 | 1.000000 | 2.375758 |
抛一枚公平的硬币,最终落在最初朝上的一面的可能性更大,这是真的吗?
证据表明这是真的!
斯坦福大学的佩尔西·迪亚科尼斯和苏珊·霍姆斯记录了10000次抛硬币实验。硬币落地时正面朝上的概率为50.8%(来源:美国数学学会期刊《数学科学动态》中的 “51%解决方案”)。出现如此高或更高比例的概率为5.48%。
为了从数学上证明这一点,我假设硬币的实际旋转次数服从泊松分布。更具体地说,如果平均旋转次数为m,那么恰好旋转n次的概率为exp(-m)*m^n/n!。为了说明泊松分布,下图显示了假设平均值为10,硬币旋转0到25次的概率。
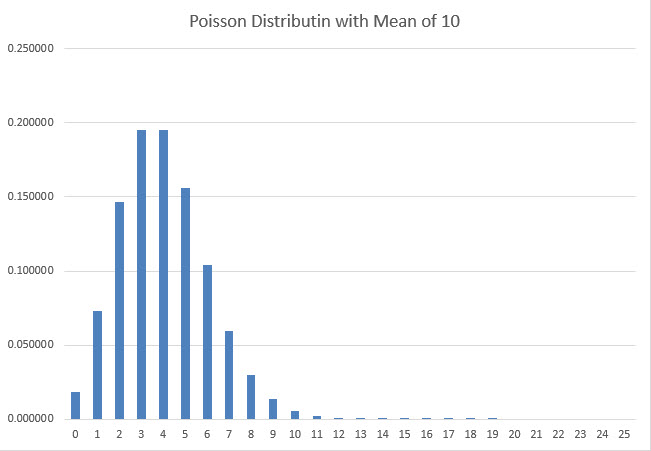
我选择泊松假设的原因是,当均值足够大时,它遵循近似钟形曲线的形状,并且实际结果永远不会低于零。
然后,我计算了不同半转均值下,半转次数为偶数(最终落地时与起始位置同一侧朝上)的概率。下表显示了均值在0.5到5.0之间的结果。
旋转次数为偶数和奇数的概率
| 平均革命 | 偶数总计 | 奇数总数 |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
我开始好奇,为什么偶数的概率总是大于 50%。事实证明,给定平均值 m,偶数的概率可以表示为 0.5 + e^(-2m)/2。e 的任意次方必定为正数,因此旋转次数为偶数的概率也为正数。
您可以在此处看到我对该公式的证明。
您对“价格猜猜猜”节目中的拼字游戏有何分析?
为了其他读者的利益,让我先介绍一下规则。
- 有一块板,上面有 30 张卡片,编号为 1 到 30。
- 每张卡片的背面都有一个字母或单词“car”。每个字母或单词的分布如下:
- C:11
- 答:11
- 评分:6
- 车:2
- 主持人让玩家选择两张牌。
- 在定价游戏之后(我不会深入讨论),玩家有机会获得最多三张卡片。
- 卡片将被翻转。
- 玩家可以通过以下两种方式赢得汽车:
- 玩家获得每个字母的至少一张卡片(从而拼出单词 CAR)。
- 玩家获得至少一张“CAR”卡。
- 在游戏的任何时候,玩家都可以投降,并为每张未翻开的牌获得 1,000 美元。
这是正在进行的比赛的片段。
下表显示了获胜的概率,根据玩家拥有的牌数计算,假设尚未翻开任何牌。
拼字比赛——获胜概率
| 牌 | 可能性 获胜 |
|---|---|
| 2 | 0.131034 |
| 3 | 0.371921 |
| 4 | 0.584018 |
| 5 | 0.734888 |
在翻开任何牌之前,玩家不应该放弃,因为假设汽车的价值合理。例如,即使只有两张牌,玩家也有13.1%的概率至少拿到一张“CAR”牌。如果汽车的价值为15,263.16美元,那么玩家应该对2,000美元的放弃价值无所谓。任何新车的价值都会高于这个数字。
以下是根据玩家未翻开的牌的数量对汽车价值的漠视点数。
拼字比赛——获胜概率
| 牌 | 漠不关心 观点 |
|---|---|
| 2 | 15,263.16 美元 |
| 3 | 8,066.23 美元 |
| 4 | 6,849.11 美元 |
| 5 | 6,803.75 美元 |


