请问巫师 #326
掷骰子游戏中的铁十字策略是什么?您对此有何看法?
铁十字是一种投注场地和位置的方式,在掷出除 7 以外的任何数字时都会获胜。场地已经涵盖了 2、3、4、9、10、11 和 12。玩家将在此基础上加上 5、6 和 8 的位置投注,以覆盖除 7 之外的其余数字。下表显示了场地投注 5 美元、5 美元位置投注 5 美元、6 美元位置投注 6 和 8 的数学计算情况。
铁十字勋章
| 骰子总数 | 赢 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 2 | 10 | 1 | 0.027778 | 0.277778 |
| 3 | 5 | 2 | 0.055556 | 0.277778 |
| 4 | 5 | 3 | 0.083333 | 0.416667 |
| 5 | 2 | 4 | 0.111111 | 0.222222 |
| 6 | 2 | 5 | 0.138889 | 0.277778 |
| 7 | -22 | 6 | 0.166667 | -3.666667 |
| 8 | 2 | 5 | 0.138889 | 0.277778 |
| 9 | 5 | 4 | 0.111111 | 0.555556 |
| 10 | 5 | 3 | 0.083333 | 0.416667 |
| 11 | 5 | 2 | 0.055556 | 0.277778 |
| 12 | 15 | 1 | 0.027778 | 0.416667 |
| 三十六 | 1.000000 | -0.250000 |
表格右下角显示预期损失为0.25美元。总投注金额为22美元。因此,总赌场优势为0.25美元/22美元=1/88=1.14%。
说到这儿,你可能会疑惑,为什么这个赌场优势会低于每次投注的赌场优势。答案是,投注6和8的赌场优势为1.52%,投注5的赌场优势为4.00%,这些优势都是基于每次投注的。如果以每次投注为单位来定义位置投注的赌场优势,那么投注6和8的赌场优势为0.46%,投注5的赌场优势为1.11%。
我们可以对所有投注进行加权平均,得出 1.14% 的赌场优势,如下所示:
($5*2.78% + $5*1.11% + $12*0.46%)/22 = $0.25/$22 = 1.14%。
警惕那些在12点的场地投注中只支付2比1赔率的赌场。坚持要求获得完整的3比1赔率。短赔率会使该投注的赌场优势从2.78%翻倍至5.56%。
在我看来,与大多数游戏相比,1.14% 的赔率已经相当不错了。然而,在掷骰子游戏中,你的赔率可以更高。例如,如果赔率为 3-4-5 倍,下注 Pass 和 Come,再加上全赔率,你的赌场优势可以降至 0.37%。反过来,下注 Don't Pass 和 Don't Come,再加上全赔率,赌场优势就会降到 0.27%。掷一个公平的骰子,每个面至少掷出两次,预期掷骰子的次数是多少?
[剧透=解决方案]
虽然这个问题可以用冗长乏味的马尔可夫链来解决,但我更喜欢用积分法。我在我的Fire Bet和Bonus Craps页面中解释了如何使用这种方法。
想象一下,重大事件不再由一次掷骰子决定,而是被视为一个时间瞬间。假设事件之间的时间间隔具有无记忆性,平均间隔为一个时间单位。换句话说,事件之间的时间间隔服从均值为1的指数分布。这对于裁决赌注来说无关紧要,因为事件仍然是一次一个地发生的。
根据泊松分布,在 x 个单位时间内,骰子任意一面掷出次数为零的概率为 exp(-x/6)*(x/6) 0 /0! = exp(-x/6)。泊松分布还表示,任意一面掷出恰好一次的概率为 exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6)。因此,任意一面在 x 个单位时间内掷出两次或两次以上概率为 1 - exp(-x/6)*(1 + (x/6))。六面掷出至少两次的概率为 (1 - exp(-x/6)*(1 + (x/6))) 6。至少有一面未掷出至少两次的概率等于:
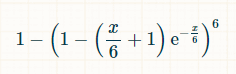
我们需要将其与所有时间结合起来,以找出平均需要多长时间才能实现预期目标。
幸运的是,我们此时可以使用积分计算器。对于链接中的那个,在“计算积分”后面的文本框中输入 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692,并在自定义下将积分的边界设置为 0 到 ∞。
答案是 390968681 / 16200000 = 约 24.13386919753086
[/spoiler]我在Wizard of Vegas论坛上提出并讨论了这个问题。
我有一个由两部分组成的问题。
对于第 1 部分,给出:- x + y + z = 1
- x^2 + y^2 + z^2 = 4
- x^3 + y^3 + z^3 = 9
x^4 + y^4 + z^4 是多少?
对于第二部分,当出现以下情况时,一般情况的答案是什么:
- x + y + z = a
- x^2 + y^2 + z^2 = b
- x^3 + y^3 + z^3 = c
你先用一个公平的六面骰子掷六次,并记录每次掷出的结果。然后,你把这些数字写在另一个没有标签的公平骰子的六个面上。例如,如果你掷出的六次结果是3、5、3、6、1和2,那么你的第二个骰子上就不会出现4,而是会出现两个3。
接下来,你把第二个骰子掷六次。把这六个数字写在另一个公平骰子上,然后继续这个过程,用前一个骰子生成一个新的骰子。
最终,你会得到一个六个面点数都相同的骰子。为了达到这个状态,从一个骰子转换到另一个骰子的平均次数是多少(或者总掷骰数除以6)?
[剧透=解决方案]
为了避免混淆,我们用字母而不是数字来标记初始骰子。我们用字母标记每个可能的骰子状态。例如,AAABBC 表示三个同种字母,两个同种字母,一个同种字母。初始状态显然是 ABCDEF。
令 E(ABCDEF) 为从状态 ABCDEF 开始的预期掷骰次数。
E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656基于从一个状态到另一个状态的组合数量,下面的转换矩阵展示了从每个初始状态(左列)到每个新状态的转换方式数量。顺便说一下,这花了几个小时才构建好。
过渡矩阵A
| 状态 前 | 啊啊啊啊啊 | AAAAB | AAAABB | AAABBB | AAAABC | AAABBC | 美国商务部商务合作委员会 | AAAABCD | ABCD | ABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AAAAB | 15,626 | 18,780 | 9,750 | 2,500 | - | - | - | - | - | - | - |
| AAAABB | 4,160 | 13,056 | 19,200 | 10,240 | - | - | - | - | - | - | - |
| AAABBB | 1,458 | 8,748 | 21,870 | 14,580 | - | - | - | - | - | - | - |
| AAAABC | 4,098 | 12,348 | 8,190 | 2,580 | 7,920 | 10,080 | 1,440 | - | - | - | - |
| AAABBC | 794 | 5,172 | 8,670 | 5,020 | 6,480 | 17,280 | 3,240 | - | - | - | - |
| 美国商务部商务合作委员会 | 192 | 2,304 | 5,760 | 3,840 | 5,760 | 23,040 | 5,760 | - | - | - | - |
| AAAABCD | 732 | 4,464 | 4,140 | 1,680 | 7,920 | 14,400 | 2,520 | 4,320 | 6,480 | - | - |
| ABCD | 130 | 1,596 | 3,150 | 1,940 | 5,280 | 16,800 | 3,600 | 4,800 | 9,360 | - | - |
| ABCDE | 68 | 888 | 1,380 | 760 | 3,960 | 11,520 | 2,520 | 7,200 | 14,040 | 4,320 | - |
| ABCDEF | 6 | 180 | 450 | 300 | 1,800 | 7,200 | 1,800 | 7,200 | 16,200 | 10,800 | 720 |
我不会长篇大论地讲解矩阵代数,只是假设矩阵 B 如下:
矩阵B
| 状态 前 | AAAAB | AAAABB | AAABBB | AAAABC | AAABBC | 美国商务部商务合作委员会 | AAAABCD | ABCD | ABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|
| AAAAB | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABB | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAABBB | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABC | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| AAABBC | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| 美国商务部商务合作委员会 | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| AAAABCD | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| ABCD | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| ABCDE | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| ABCDEF | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
答案是矩阵 B 的行列式与矩阵 A 的行列式之比:
确定(A)= 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000,000
确定(B)= 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000,000
Determ(B) / Determ(A) = 约 9.65599148388557
[/spoiler]

