请问巫师 #322
我坐在一局德州扑克桌前,牌局进行时,高手拿到了同花顺。桌上另外两位玩家说,这是连续第三张同花顺。这概率是多少?
在一场10人参与的德州扑克游戏中,假设无人弃牌,那么高手牌为顺子或同花大顺的概率是350.14分之一。三局中有三局出现这种情况的概率是42,926,491分之一。
然而,那张牌桌可能已经玩了好几个小时了。或许更现实的问题是,这种情况在一天中至少发生一次的概率是多少。假设整整24小时都在玩,每小时24手牌,那么这个问题的答案是59,621分之一。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
假设策略正确,在终极德州扑克中,如果玩家加注4倍,获胜的概率是多少?我记录了96手4倍牌局。不算平局,我赢了66手,输了30手。这与预期相比如何?
假设 4 倍加注策略正确,则在 4 倍加注的情况下,每个结果的概率为:
- 胜率:58.82%
- 亏损:38.47%
- 平局:2.72%
如果排除平局因素,胜率是60.46%。在96手牌中,4倍胜的预期次数为58.04次。因此,66次胜率略高于预期,但幅度并不显著。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
阿克塞尔和鲍勃各自有一副52张的牌。两人都随机洗牌。然后,他们同时从每副牌中翻出一张牌。他们同时翻出同一张牌至少一次的概率是多少?
答案很容易估算为 1-(51/52) 52 = 0.63568648。然而,估算在智力上实在难以令人满意。所以,让我们来求一个精确的解吧!
步骤 1:首先,考虑第二副牌的排序方式数,其中第一张牌是 1。答案是排序其他 51 张牌的方式数,即 51!= 1551118753287382280224243016469303211063259720016986112000000000000。
任何牌都能匹配第一副牌,所以我们必须对所有 52 张牌都进行同样的操作。这样一来,就有 52*51! = 52! 种组合,其中至少有一张牌匹配。
步骤 2:然而,步骤 1 会重复计算两张牌匹配的所有情况。例如,如果前两张牌是 1 和 2,那么我们需要将其他牌的 50! 种排列方式计算两次,第一次将 1 作为第一张牌,第二次将 2 作为第二张牌。从 52 张牌中选择 2 张牌的方式数为 combin(52,2) = 1326。对于每两张牌的组合,其他牌的排列方式有 50! = 3041409320171337804361260816606476884437764156896051200000000000000 种。因此,对于步骤 2,我们需要减去 combin(52,2)*50! = (52*51/2!)*50! = 52!/2! 种组合。
步骤 3:接下来,考虑随机牌堆中前三张牌的顺序为 1、2 和 3 的情况。其余 49 张牌有 49! 种排序方法。在初始步骤中,我们会数三次,以找出至少一张匹配的牌。然后,在第二步中,我们会减去所有 combin(3,2)=3 种从这三张牌中选择 2 张的方法。因此,这种情况会被计算 3-3=0 次,因此我们需要将它们加回去。有 combin(52,3) 种选择至少 3 张匹配牌的情况。因此,我们需要重新添加 combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! 种组合。
步骤 4:接下来,考虑随机牌堆中前四张牌的顺序为 1、2、3 和 4 的情况。其余 48 张牌有 48! 种排序方法。在初始计数至少一张匹配牌的步骤中,我们需要数四次。然后,在步骤 2 中,我们需要减去所有 combin(4,2)=6 种从这四张牌中选择两张的方法。然后,我们需要加上所有 combin(4,3)=4 种从这四张牌中选择三张的方法。因此,每种情况都有 4-6+4=2 种计数方法。因此,我们需要减去其中一种计数方法,使每种情况都只计算一次。共有 combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! 种需要加回去的情况。
我们将继续这样做,交替进行加法和减法来纠正重复计算。
最后,随机牌堆中至少有一张牌与有序牌堆匹配的情况数量 = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783。
共有 52 种方法可以排列 52 张牌!= y = 5271776154963652194226185415451226599692124538619822080000000000000 种方法可以排列 52 张牌。
因此,答案是 x/y = 0.6321205588285576784044762298
没有匹配的概率是 1-(x/y) = 0.3678794411714423215955237702。
如果这个数字看起来很熟悉,那就对了。1/e = 0.3678794411714423215955237702。
因此,答案可以非常接近地估计为 1-(1/e)。
致谢
数学计算是在Pari/GP中进行的
这个问题已在我的Wizard of Vegas论坛中提出并讨论过。
在您网站上名为宾果模式概率(PDF) 的文档中,您指出,假设游戏中有 300 张牌,那么找到获胜者的预期呼叫次数如下:
- 四角球:8.43
- 小钻石:11.833
两种模式都只需要四个标记,并且只有一种获胜方式。为什么获胜所需的球数不同?
这个问题很难解释。首先,我想说的是,单张牌游戏中的预期叫牌次数是一样的。然而,多张牌游戏中存在相关效应。
这个问题很难快速回答,但如果硬要回答,那是因为四角图案需要球集中在B列和O列。而小菱形图案则更容易在B、N和O列上更均匀地分布球。
让我们把游戏简化成无限多张牌,并且每次抽球都会放回原位。以下是两种游戏中获胜所需的球数:
- 四个角:2.5+2.5+((1/2)*10+(1/2)*(2.5+5)) = 13.75
- 小钻石:=(5/3)+((1/3)*((5/3)+(5/2)+5)+(2/3)*((5/2)+((1/2)*((5/2)+5)+(1/2)*(5+5)))) = 12 + 2/9
这表明四个角球多花了 1.53 个球。
根据正常的宾果游戏规则,通过模拟运行此程序,假设有无限张牌,结果如下:
- 四角:12.8289
- 钻石:11.3645
这次相差 1.46 个球。
我希望展示的是,如果标记分布在更多列上,图案更容易被覆盖。因此,我认为在单排宾果游戏中,你通常会看到获胜的宾果图案是水平的。
这个问题是在我的“拉斯维加斯巫师”论坛中讨论过的。
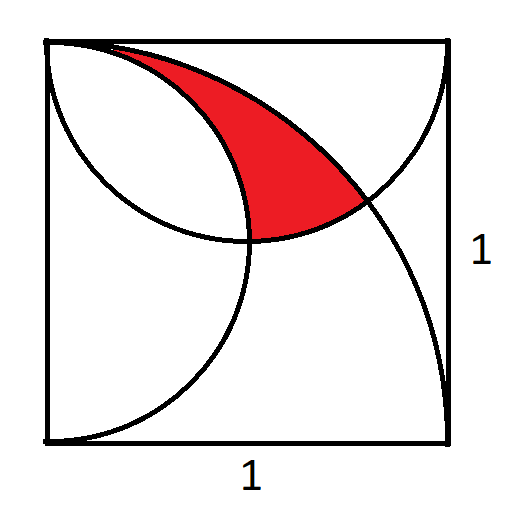
上图中,边长为1的正方形中有一个四分之一圆和两个半圆。请问红色区域的面积是多少?
点击以下按钮查看我的答案。
[spoiler=答案](3/8)*asin(4/5)-(1/4)=~0.0977357067506052[/剧透]单击以下按钮查看我的解决方案。
[剧透=解决方案]这是我的解决方案的链接。(PDF)
我在Wizard of Vegas论坛上提出并讨论了这个问题。
致谢:我要感谢Mind Your Decisions提供这个数学谜题。


