请问巫师 #313
提醒其他读者,埃及艳后基诺的玩法与传统基诺类似,但如果最后抽出的球与玩家选择的球之一匹配并获胜,则玩家还将赢得12次免费游戏,乘数为2倍。免费游戏并不能获得更多免费游戏。
您没有指定选号数量或赔付表,所以我们以3-10-56-180-1000选号-8赔付表为例。首先,让我们计算一下回报。
在基诺游戏中,从 y 个球中接住 x 个球的方法数,就是从 20 个球中接住 x 个球,从 60 个球中接住 yx 个球的方法数。用 Excel 表达式表示,这等于 combin(20,x)*combin(60,yx)。再提醒一下,combin(x,y) = x!/(y!*(xy)!)。最终 x! = 1*2*3*...*x。
回顾完毕,以下是该赔付表的回报率表。右列显示的是预期赢利平方,我们稍后会用到。
Pick 8 基诺
| 事件 | 支付 | 组合 | 可能性 | 返回 | 返回^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2,558,620,845 | 0.088266 | 0.000000 | 0.000000 |
| 1 | 0 | 7,724,138,400 | 0.266464 | 0.000000 | 0.000000 |
| 2 | 0 | 9,512,133,400 | 0.328146 | 0.000000 | 0.000000 |
| 3 | 0 | 6,226,123,680 | 0.214786 | 0.000000 | 0.000000 |
| 4 | 3 | 2,362,591,575 | 0.081504 | 0.244511 | 0.733533 |
| 5 | 10 | 530,546,880 | 0.018303 | 0.183026 | 1.830259 |
| 6 | 56 | 68,605,200 | 0.002367 | 0.132536 | 7.422014 |
| 7 | 180 | 4,651,200 | 0.000160 | 0.028882 | 5.198747 |
| 8 | 1000 | 125,970 | 0.000004 | 0.004346 | 4.345661 |
| 全部的 | 28,987,537,150 | 1.000000 | 0.593301 | 19.530214 |
接下来,我们来计算一下平均奖金。从上表可以看出,不计奖金的平均赢利为0.593301。在奖金中,玩家可以获得12次双倍免费旋转。因此,奖金的预期赢利为2×12×0.593301 = 14.239212。
接下来,我们来计算一下赢得奖金的概率。如果玩家抓到四个数字,那么第20个球是这四个数字之一的概率是4/20。一般来说,如果玩家抓到c个数字,那么第20个球对中奖有帮助的概率是c/20。
赢得奖金的公式为:概率(第 4 组)*(4/20) + 概率(第 5 组)*(5/20) + 概率(第 6 组)*(6/20) + 概率(第 7 组)*(7/20) + 概率(第 8 组)*(8/20)。我们可以从上面的回报表中知道任何特定获胜的概率。因此,赢得奖金的概率为:
0.081504*(4/20) + 0.018303*(5/20) + 0.002367*(6/20) + 0.000160*(7/20) + 0.000004*(8/20) = 0.021644。
通过赢得奖金的概率和平均奖金赢额,我们可以计算出奖金的回报为 0.021644 × 14.239212 = 0.308198。
我们不需要知道,但游戏的总体回报是基础游戏的回报加上奖金的回报,等于 0.593301 + 0.308198 = 0.901498。
现在,让我们开始讨论实际的方差。提醒一下,方差的一般公式是:
var(x + y) = var(x) + var(y) + 2*cov(x,y),其中 var 代表方差,cov 代表协方差。在这个游戏中:
总方差 = var(基础游戏)+ var(奖励)+ 2*cov(基础游戏和奖励)。
方差的基本公式是 E(x^2) - [E(x)]^2。换句话说,就是预期赢利的平方减去预期赢利的平方。
话虽如此,我们先从基础游戏的方差开始。还记得我之前说过,我们需要第一个表格中的预期赢利平方吗?第一个表格的右下角单元格显示预期赢利平方为 19.530214。我们已经知道预期赢利是 0.593301。因此,基础游戏的方差为 19.530214 - 0.593301 2 = 19.178208。
接下来,我们来计算奖金的方差(假设已经中奖)。为此,回想一下:
var(ax) = a 2 x,其中 a 为常数。
还记得 n 个随机变量 x 的方差是 nx。
也就是说,如果 x 是奖励游戏中的基础赢利,那么整个奖励的方差为 2 (2) × 12 (x)。从上文可知,基础游戏中单次旋转(不计奖励)的方差为 19.178208。因此,假设已经获得奖励,则奖励的方差为 2 (2) × 12 (x) × 19.178208 = 920.554000。
然而,我们需要知道的是第一个球被抽出之前奖金的方差,包括根本得不到奖金的可能性。不,我们不能简单地将奖金的方差乘以中奖概率。相反,回想一下var(x) = E(x^2) - [E(x)]^2。我们将其重新排列如下:
E(x^2) = var(x) + [E(x)]^2
我们知道奖金的平均值和方差,因此奖金的预期赢利平方为 920.554000 + 19.178208 2 = 1123.309169。
因此,在抽出第一个球之前,奖金赢取的预期平方是 prob(bonus) × E(x^2) = 0.021644 × 1123.309169 = 24.313239。
我们已经计算出,在第一球开球前,奖金的预期赢利为0.308198。因此,在第一球开球前,奖金的总体方差为24.313239 - 0.308198 2 = 24.218253。
下一步是计算协方差。你可能会问:“为什么基础奖金和奖励奖金之间存在相关性?” 这是因为最后一个抽出的球必须对奖金产生贡献才能触发奖励。假设最后一个球对奖金产生贡献,平均奖金就会增加。提醒一下,贝叶斯条件概率公式如下:
P(A 给定 B) = P(A 和 B)/P(B)。
然后,假设最后一个球被击中,让我们重新为基础游戏的回报表:
Pick 8 Keno 给出最后一球击中
| 事件 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|
| 0 | 0 | - | 0.000000 | 0.000000 |
| 1 | 0 | - | 0.000000 | 0.000000 |
| 2 | 0 | - | 0.000000 | 0.000000 |
| 3 | 0 | - | 0.000000 | 0.000000 |
| 4 | 3 | 472,518,315 | 0.753119 | 2.259358 |
| 5 | 10 | 132,636,720 | 0.211402 | 2.114019 |
| 6 | 56 | 20,581,560 | 0.032804 | 1.837010 |
| 7 | 180 | 1,627,920 | 0.002595 | 0.467036 |
| 8 | 1000 | 50,388 | 0.000080 | 0.080310 |
| 全部的 | 627,414,903 | 1.000000 | 6.757734 |
右下角单元格显示,假设最后一个球被击中,平均胜利为 6.757734。
接下来,回想一下你在大学统计课上学到的内容:
cov(x,y) = exp(xy) - exp(x)*exp(y) 。
在我们的例子中,设 x = 基础游戏胜利,y = 奖励胜利。我们先来计算 exp(xy)。
Exp(xy) = prob(赢得的奖金)*(赢得奖金时的平均基础游戏胜利)*average(奖金胜利) + prob(未赢得的奖金)*(未赢得奖金时的平均基础游戏胜利)*average(未赢得奖金时的平均奖金胜利)。 很容易得出 average(未赢得奖金时的平均奖金胜利) = 0,因此我们可以将其重写为:
Exp(xy) = prob(赢得的奖金)*(赢得奖金后的平均基础游戏胜利)*平均值(赢得的奖金) =
0.021644 × 6.757734 × 14.239212 = 2.082719。我们已经求解了 E(x) 和 E(y),因此协方差是:
cov(x,y) = exp(xy) - exp(x)*exp(y) = 2.082719 - 0.593301 × 0.308198 = 1.899865。
让我们回到涉及协方差时的方差总体方程:
总方差 = var(基础游戏) + var(奖励) + 2*cov(基础游戏和奖励) = 19.178208 + 24.218253 + 2×1.899865 = 47.196191。标准差是其平方根,即 6.869948。
好了,就这样吧。这个花了我好几个小时,希望你满意。
我在Wizard of Vegas论坛上提出并讨论了这个问题。
我听说,在美国,离婚率通常为50%,这个数字是用同一时期内离婚数量与结婚数量之比来计算的。是这样吗?您认为这种统计方法公平吗?我对此表示怀疑,因为您研究的是短期内的离婚数量,而不是长期婚姻的数量。
如果人口和年龄分布稳定,那么如果离婚概率真的是 50%,那么在样本量较大的情况下,我们预计在任何给定的时间段内都会看到一起离婚与两起结婚的比例。
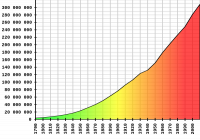
然而,人口并不稳定。从这张图表来看,美国人口每十年增长10.71%,相当于每年1.02%。为了简单起见,我们就假设是1%吧。
地图来源:美国人口普查
据fatherly.com称,失败的婚姻平均持续 8 年。
如果您观察到目前离婚与结婚的比例为 1 比 2,那么任何特定婚姻以离婚告终的平均概率是多少?
我们现在看到的离婚案例是8年前结婚的,当时的人口比例是现在的92.35%。简单的计算表明,真实的离婚概率是54.14%。
我们来检查一下。
首先,根据疾病预防控制中心的数据,每年每1000人中就有6.9对结婚。这个数字与本文的问题无关,但我认为有助于理解所涉及的数字。
假设8年前人口为3亿,那么当年结婚的人数为0.69%*3亿=207万对。
如果其中 54.14% 的人在八年后以离婚告终,那么我们现在将看到 2,070,000 * 54.14% = 1,120,698 起离婚事件。
1,120,698 / 2,070,000 = 目前观察到的离婚与结婚比率的 50%。
免得有人说,是的,我知道并非所有离婚都会在八年内结束。然而,综合考虑,我认为最终结果与我54.14%的真实离婚率相差无几。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
你的办公室有100名员工,他们会举行一个秘密圣诞礼物交换活动。你会把每个人的名字写在一张纸上,然后把纸放进一顶帽子里,然后每个人随机抽取一个名字作为礼物送给他们。
问题是,平均下来会有多少个闭环?比如说,戈登把钱给了唐,唐又给了乔恩,乔恩又给了内森,内森又给了戈登。或者抽自己的名字。
假设每个人每次选择一个。每个人选择时,会出现两种情况:
- 挑选者的名字已经被挑选了。
- 挑选者的名字仍然在名字箱里。
对于任何给定的挑选者,假设还有 n 个人需要挑选。
如果正在挑选名字的人的名字已经被选中,那么挑选者有 1/n 的概率会选择与他名字相关的名字,从而形成一个闭环。例如,假设艾米正在挑选。艾米的名字已经被鲍勃占据,鲍勃的名字已经被查理占据,而查理的名字仍然在箱子里。由于箱子里还有 n 个名字,所以艾米选择查理名字的概率为 1/n,从而形成一个闭环。
如果选择者的名字尚未被选中,那么艾米选择自己名字的概率为 1/n,从而形成一个循环。
无论如何,如果拾取者没有完成一个循环,她就加入了另一个链条的一部分,而这个链条最终会被其他人完成。每个链条在完成时只应被计算一次。
因此答案是 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518。
对于任何足够多的玩家数量 n 的估计值是 ln(n)。
这个问题是在我的Wizard of Vegas论坛中提出并讨论的。
玩视频老虎机时,额外的百搭保证值多少钱?
这取决于很多因素。我的理解是,如果一个额外的百搭符号比玩家通常获得的平均数字高出多少,它的价值是多少。虽然答案因游戏而异,但一个重要因素是屏幕上的行数。如果屏幕上有三行,额外的百搭符号将影响1/3的赔付线。同样,如果屏幕上有四行,它的价值就会降低,影响1/4的赔付线。
为了回答你的问题,我研究了之前已经解构过的游戏《埃及艳后》 。下表显示了百搭符号的预期值相对于随机百搭符号数量的增长情况。
埃及艳后中的额外狂野价值
| 卷轴 | 3 行 | 4 行 |
|---|---|---|
| 1 | 95.71% | 71.79% |
| 2 | 99.76% | 74.82% |
| 3 | 76.24% | 57.18% |
| 4 | 21.25% | 15.93% |
| 5 | 1.96% | 1.47% |