请问巫师 #284
你听说过西雅图一家汽车经销商因为海鹰队完封巨人队而赔了42万美元的事吗?我听说他们为此买了7000美元的保险。那么合理的保费是多少呢?
根据文章《 华盛顿汽车经销商在海鹰队完封巨人队后赔付 420,000 美元》报道,该经销商推出了一项促销活动,如果海鹰队在 2013 年 12 月 15 日举行的第 15 周比赛中完封巨人队,则将向 12 名获胜者每人支付 35,000 美元。文章还说,如果真的发生了上述事件,该经销商还支付了 7,000 美元的保险费。
根据1983年至2012赛季的每场NFL比赛,每场比赛都有特定一方被完封。然而,作为一支落后7分的弱队,在一场平均得分高于/低于的比赛中,我认为巨人队被完封的概率高于平均水平。那场比赛的得分高于/低于41分。让我们用一些代数运算来计算巨人队的预期得分。
让:
s=海鹰队得分
g=巨人队积分
根据点差和总分高/低,我们知道 s+g=41 和 s=g+7。
将第二个方程代入第一个方程:
(g+7) + g = 41
2克+7=41
2克=34
g = 17
接下来,让我们根据1983年至2012赛季的数据,根据每支球队的预计得分来计算完封的概率。我跳过了样本量为零的行。
完封概率
| 估计的 积分 | 样本量 | 完封 | 比率 |
|---|---|---|---|
| 5.25 | 1 | 0 | 0.0% |
| 6.50 | 1 | 0 | 0.0% |
| 7.75 | 1 | 0 | 0.0% |
| 8.00 | 1 | 0 | 0.0% |
| 8.25 | 3 | 0 | 0.0% |
| 8.50 | 2 | 0 | 0.0% |
| 8.75 | 2 | 0 | 0.0% |
| 9.00 | 2 | 0 | 0.0% |
| 9.50 | 4 | 0 | 0.0% |
| 9.75 | 6 | 1 | 16.7% |
| 10.00 | 10 | 1 | 10.0% |
| 10.25 | 7 | 0 | 0.0% |
| 10.50 | 14 | 2 | 14.3% |
| 10.75 | 7 | 1 | 14.3% |
| 11.00 | 十三 | 1 | 7.7% |
| 11.25 | 21 | 1 | 4.8% |
| 11.50 | 22 | 3 | 13.6% |
| 11.75 | 23 | 1 | 4.3% |
| 12.00 | 三十四 | 2 | 5.9% |
| 12.25 | 三十六 | 7 | 19.4% |
| 12.50 | 41 | 3 | 7.3% |
| 12.75 | 三十九 | 4 | 10.3% |
| 13.00 | 55 | 1 | 1.8% |
| 13.25 | 58 | 5 | 8.6% |
| 13.50 | 78 | 1 | 1.3% |
| 13.75 | 89 | 5 | 5.6% |
| 14.00 | 92 | 4 | 4.3% |
| 14.25 | 108 | 7 | 6.5% |
| 14.50 | 117 | 8 | 6.8% |
| 14.75 | 141 | 7 | 5.0% |
| 15.00 | 160 | 7 | 4.4% |
| 15.25 | 160 | 7 | 4.4% |
| 15.50 | 213 | 7 | 3.3% |
| 15.75 | 198 | 11 | 5.6% |
| 16.00 | 206 | 6 | 2.9% |
| 16.25 | 221 | 12 | 5.4% |
| 16.50 | 241 | 10 | 4.1% |
| 16.75 | 273 | 7 | 2.6% |
| 17.00 | 306 | 8 | 2.6% |
| 17.25 | 305 | 8 | 2.6% |
| 17.50 | 306 | 10 | 3.3% |
| 17.75 | 323 | 4 | 1.2% |
| 18.00 | 299 | 8 | 2.7% |
| 18.25 | 332 | 8 | 2.4% |
| 18.50 | 309 | 9 | 2.9% |
| 18.75 | 307 | 7 | 2.3% |
| 19.00 | 356 | 8 | 2.2% |
| 19.25 | 389 | 5 | 1.3% |
| 19.50 | 361 | 5 | 1.4% |
| 19.75 | 343 | 6 | 1.7% |
| 20.00 | 402 | 8 | 2.0% |
| 20.25 | 379 | 6 | 1.6% |
| 20.50 | 359 | 3 | 0.8% |
| 20.75 | 353 | 5 | 1.4% |
| 21.00 | 344 | 1 | 0.3% |
| 21.25 | 317 | 3 | 0.9% |
| 21.50 | 341 | 2 | 0.6% |
| 21.75 | 331 | 1 | 0.3% |
| 22.00 | 369 | 1 | 0.3% |
| 22.25 | 336 | 0 | 0.0% |
| 22.50 | 316 | 2 | 0.6% |
| 22.75 | 280 | 3 | 1.1% |
| 23.00 | 311 | 1 | 0.3% |
| 23.25 | 290 | 3 | 1.0% |
| 23.50 | 279 | 1 | 0.4% |
| 23.75 | 255 | 1 | 0.4% |
| 24.00 | 246 | 1 | 0.4% |
| 24.25 | 219 | 0 | 0.0% |
| 24.50 | 230 | 2 | 0.9% |
| 24.75 | 230 | 1 | 0.4% |
| 25.00 | 212 | 2 | 0.9% |
| 25.25 | 207 | 0 | 0.0% |
| 25.50 | 176 | 1 | 0.6% |
| 25.75 | 154 | 0 | 0.0% |
| 26.00 | 154 | 1 | 0.6% |
| 26.25 | 113 | 0 | 0.0% |
| 26.50 | 137 | 0 | 0.0% |
| 26.75 | 122 | 0 | 0.0% |
| 27.00 | 95 | 0 | 0.0% |
| 27.25 | 98 | 0 | 0.0% |
| 27.50 | 83 | 0 | 0.0% |
| 27.75 | 81 | 0 | 0.0% |
| 28.00 | 82 | 0 | 0.0% |
| 28.25 | 55 | 1 | 1.8% |
| 28.50 | 56 | 0 | 0.0% |
| 28.75 | 51 | 0 | 0.0% |
| 29.00 | 四十八 | 0 | 0.0% |
| 29.25 | 三十四 | 0 | 0.0% |
| 29.50 | 24 | 0 | 0.0% |
| 29.75 | 二十五 | 0 | 0.0% |
| 30.00 | 24 | 0 | 0.0% |
| 30.25 | 21 | 0 | 0.0% |
| 30.50 | 18 | 0 | 0.0% |
| 30.75 | 23 | 0 | 0.0% |
| 31.00 | 16 | 0 | 0.0% |
| 31.25 | 15 | 0 | 0.0% |
| 31.50 | 8 | 0 | 0.0% |
| 31.75 | 3 | 0 | 0.0% |
| 32.00 | 6 | 0 | 0.0% |
| 32.25 | 7 | 0 | 0.0% |
| 32.50 | 6 | 0 | 0.0% |
| 32.75 | 3 | 0 | 0.0% |
| 33.00 | 4 | 0 | 0.0% |
| 33.25 | 6 | 0 | 0.0% |
| 33.50 | 5 | 0 | 0.0% |
| 34.75 | 4 | 0 | 0.0% |
| 35.00 | 2 | 0 | 0.0% |
| 35.50 | 1 | 0 | 0.0% |
| 36.00 | 2 | 0 | 0.0% |
| 36.25 | 1 | 0 | 0.0% |
| 36.50 | 1 | 0 | 0.0% |
| 37.25 | 1 | 0 | 0.0% |
| 37.75 | 2 | 0 | 0.0% |
| 42.25 | 1 | 0 | 0.0% |
接下来的步骤太复杂,无法在此解释,但我根据估计的点数,开发了一个计算完封概率的公式。
p = 估计点数。
x = 1.562545 -0.302485 * p
完封概率 = e x /(1+e x )
下图显示了 14 至 22 分之间完封的实际概率和估计概率。
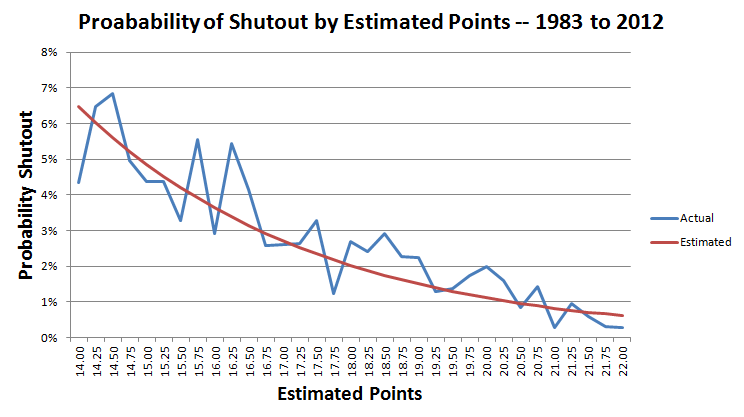
在本场比赛中巨人队预计得分 17 分。
使用表格上方的公式:
x = 1.562545 -0.302485 * 17 = -3.579706
完封概率 = exp(-3.579706)/( exp(-3.579706)+1) = 2.71%。确切地说,是 0.0271275。
考虑到如果巨人队完封对手,经销商将需要支付42万美元,那么保单的合理成本应该是42万美元×0.0271275=11394美元。通常情况下,承保此类特殊促销活动的保险公司会将合理成本翻倍,所以我预计保费应该在22788美元左右。所以,经销商支付的7000美元保费简直是便宜。假设老板仔细核算了一下,我可不想成为计算出这7000美元保费的人。
这个问题是在我的“拉斯维加斯巫师”论坛中提出并讨论的。
不存在最大素数的证明是什么?
假设存在一个最大的素数。我们可以将这些素数编号为 p1=2,p2=3,p3=5,p4=7,……pL = 最大的素数。
现在让我们定义数字 x = p1*p2*p3*p4*...*pL + 1。
素数的含义是没有其他比它小的素数可以整除它。
如果我们用 p1、p2、p3、... pL 除以 x,每次都会得到余数 1。
你可能会争辩说,一个大于 pL 的素数也许能被 x 整除。没错,但这样一来,你就找到了一个比所谓的最大素数更大的素数。如果不是,那么 x 就变成了一个新的最大素数,从而通过反证法证明了最初关于存在最大素数的猜想。
这个问题是在我的Wizard of Vegas论坛中提出并讨论的。
您是否同意 Business Insider 上题为“数学告诉你现在应该买一张百万大奖彩票”的文章?
不,我不同意。这是一篇糟糕的新闻报道,Business Insider 应该为此感到羞愧。
首先,这篇文章发表于2013年12月17日,即当晚6.36亿美元开奖之前。让我们用数学方法评估一下一张1美元彩票的价值。下表显示了6.36亿美元头奖所有可能结果的概率和预期回报,其中未考虑一次性罚款、税费和奖金分配等因素。由于数字较小,前三个概率以科学计数法表示。
超级百万大奖——6.36亿美元
| 抓住 | 超级球 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|---|
| 5 | 是的 | 6.36亿美元 | 1 | 3.86E-09 | 2.456634 |
| 5 | 不 | 100万美元 | 14 | 5.41E-08 | 0.054077 |
| 4 | 是的 | 5,000 美元 | 350 | 1.35E-06 | 0.006760 |
| 4 | 不 | 500美元 | 4,900 | 0.000019 | 0.009463 |
| 3 | 是的 | 50美元 | 24,150 | 0.000093 | 0.004664 |
| 3 | 不 | 5美元 | 338,100 | 0.001306 | 0.006530 |
| 2 | 是的 | 5美元 | 547,400 | 0.002114 | 0.010572 |
| 1 | 是的 | 2美元 | 4,584,475 | 0.017708 | 0.035416 |
| 0 | 是的 | 1美元 | 12,103,014 | 0.046749 | 0.046749 |
| 失败者 | 0美元 | 241,288,446 | 0.932008 | 0.000000 | |
| 全部的 | 258,890,850 | 1.000000 | 2.630865 | ||
这表明,一张1美元的彩票将获得2.630864美元的回报。扣除彩票成本后的预期利润为1.630864美元。Business Insider的利润为1.632029美元。虽然差额为0.001164美元,但并不算什么。
然而,有三件事会显著降低其价值:
- 一次性罚款。
- 税收。
- 分享奖金。
让我们逐一看一下。
大型彩票累积奖金通常以约30年期的年金形式发放,包括超级百万彩票 (Mega Millions)。如果中奖者想一次性获得所有奖金(大多数人都这么做),就必须接受大幅减免。这很公平,因为今天的一美元比未来的一美元更值钱。在2013年12月17日的开奖中,总奖金减少至3.476亿美元,相当于公布奖金的54.65%。
接下来,我们来看看税收。联邦边际所得税率最高为39.6%。州税从0%到12.3%不等,所以我们假设平均税率为6%。扣除45.6%的税款后,剩余1.891亿美元。
现在是最棘手的部分——奖金分享。值得注意的是,从 2013 年 10 月 22 日的抽奖开始,Mega Millions 将规则改为 75-15 格式,即从 1 到 75 中抽取五个号码,然后从 1 到 15 的另一个号码池中抽取一个号码。这将中奖概率降低到 258,890,850 分之一,显然是为了获得更大的奖金。仅查看此后的 17 次抽奖,使用LottoReport.com的奖金和销售数据,我发现奖金数额和需求之间存在指数关系。顺便说一下,我在强力球彩票中也发现了同样的情况。使用指数回归,我计算售出彩票总数(以百万计)的公式是 12.422 × exp(0.0052 × j),其中 j 是奖金数额(以百万计)。例如,如果头奖金额为 6.36 亿美元,预期销售额为 12.422 * exp(0.0052*636) = 3.392 亿美元。实际销售额为 3.37 亿美元,非常接近。
根据实际售出的彩票数量 336,545,306 张,我们预计中奖人数为 336,545,306/258,890,850 = 1.300 人。关键问题是,如果您中奖了,预计会有多少人分享奖金?根据泊松分布,这个问题很容易回答。假设平均中奖人数为 1.3 人,那么恰好有 x 人中奖的概率为 exp(1.3)×1.3 x /fact(x)。下表列出了 0 到 10 位其他中奖者的概率、您在每种情况下获得的奖金份额以及假设您中奖后的预期份额。
预计奖金分配比例平均为 1.3 名其他获奖者
| 其他获奖者 | 可能性 | 累积奖金份额 | 预期份额 |
|---|---|---|---|
| 10 | 0.000001 | 0.090909 | 0.000000 |
| 9 | 0.000008 | 0.100000 | 0.000001 |
| 8 | 0.000055 | 0.111111 | 0.000006 |
| 7 | 0.000339 | 0.125000 | 0.000042 |
| 6 | 0.001827 | 0.142857 | 0.000261 |
| 5 | 0.008431 | 0.166667 | 0.001405 |
| 4 | 0.032429 | 0.200000 | 0.006486 |
| 3 | 0.099786 | 0.250000 | 0.024946 |
| 2 | 0.230283 | 0.333333 | 0.076761 |
| 1 | 0.354295 | 0.500000 | 0.177148 |
| 0 | 0.272545 | 1.000000 | 0.272545 |
| 全部的 | 1.000000 | 0.559602 |
右下角的单元格显示,您可以保留 55.96% 的资金,其余 44.04% 将归于那些您必须与之分享的其他获胜者。
现在,我们的6.36亿美元头奖已降至1.891亿美元 × 55.96% = 1.058亿美元。让我们看看以这个数字作为头奖,回报表会是什么样子。
超级百万大奖——1.058亿美元
| 抓住 | 超级球 | 支付 | 组合 | 可能性 | 返回 |
|---|---|---|---|---|---|
| 5 | 是的 | 1.058亿美元 | 1 | 3.86E-09 | 0.408666 |
| 5 | 不 | 100万美元 | 14 | 5.41E-08 | 0.054077 |
| 4 | 是的 | 5,000 美元 | 350 | 1.35E-06 | 0.006760 |
| 4 | 不 | 500美元 | 4,900 | 0.000019 | 0.009463 |
| 3 | 是的 | 50美元 | 24,150 | 0.000093 | 0.004664 |
| 3 | 不 | 5美元 | 338,100 | 0.001306 | 0.006530 |
| 2 | 是的 | 5美元 | 547,400 | 0.002114 | 0.010572 |
| 1 | 是的 | 2美元 | 4,584,475 | 0.017708 | 0.035416 |
| 0 | 是的 | 1美元 | 12,103,014 | 0.046749 | 0.046749 |
| 失败者 | 0美元 | 241,288,446 | 0.932008 | 0.000000 | |
| 全部的 | 258,890,850 | 1.000000 | 0.582898 | ||
右下角单元格显示预期回报率为 58.29%。换句话说,你投资 1 美元,预期能获得约 58 美分的回报,预期损失(或赌场优势)约为 42%。这听起来像是在告诉你应该买彩票吗?
文章称,“因此,只要售出的彩票数量少于 7.3 亿张(目前这种情况很有可能发生),彩票的预期价值就应该为正,因此您应该考虑今天购买一张百万大奖彩票。”
虽然销量远低于7.3亿,但这个数字仍然很糟糕。不过,平心而论,文章接下来还说了以下内容:
请记住,这项分析有很多需要注意的地方。税收可能会严重影响你的预期收益——联邦政府将收取约40%的税款,而你的家乡州则会收取0%到13%左右的税款。
很多人都在买彩票,正如上文所讨论的,这将大大增加平局的概率,并减少随之而来的赔付。”——《商业内幕》
这些都是非常重要的警告!它们不应该只是在文章末尾顺便提及,而应该从一开始就纳入分析之中。
不是你问的,但我发现数学告诉你永远不要玩超级百万彩票。考虑到彩票需求呈指数级增长,根据头奖金额,我认为最佳投注时机是5.45亿美元的头奖。如果头奖金额超过这个数字,你就得和太多其他中奖者分享了。在这个头奖金额下,玩家预期回报率为60.2%,损失为39.8%。这已经是最好不过了。
最后,不,我不同意《商业内幕》用耸人听闻的标题欺骗读者,并且没有对税收和奖金分配进行适当的分析。
我在Wizard of Vegas论坛上提出并讨论了这个问题。


