请问巫师 #261
什么样的动态会影响⾜球总分的押注、当球季进⾏当时, 天⽓会变坏、还 有更多关于球队最近表现的资讯?有多容易(或多难)去发现赌盘的错误?
为了协助回答这个问题, 我画出NFL美式⾜球每周的平均得分数, 基于 1983-2009年每个球季。以下的图表显⽰其结果。
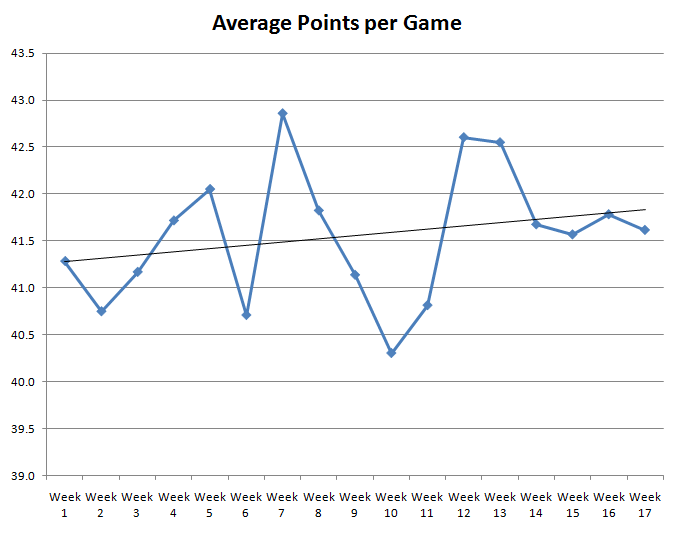
你可以看⻅, 曲线是起起伏伏的。⿊⾊实线是least-squared best fit line最 ⼩平⽅误差的回归线, 总体来说是朝上的趋势。所以当球季进⾏时, ⽓温下 降, 平均得分渐渐增加, 不过那可能轻易是因为随机的变化。
这是⺫前为⽌我所能说的。针对天⽓影响运动押注的⼀般意⻅, 我转给我 的朋友Jason Been, 他是这个议题的专家。在这⾥他曾说过:
在⼤多数案例, ⻛是天⽓最主要影响⽐赛的因素; 不过, 这并⾮唯⼀的⼀项 因素。在棒球与其他的户外运动, 阴影可以是相同的效应, 尤其是在球季早 期与晚期的下午⽐赛。下⾬或下雪在⾜球来说、并⾮⼤多数⼈所想的那 般、会是很⼤的因素, 因为同样都会影响到攻击与防守的两⽅。⼀个案例 将会是防守⽅对抗⻓程的接球者。下⾬和下雪将会同样拖延双⽅, 因此不 会有哪⼀⽅得到优势。⻛在⾜球踢球时可以消除传球的效⼒。我就⻅过⽐ 赛当中, 传球的⼀⽅被逼着在强劲侧⻛当下每次都得要跑着传球。这并不 常发⽣, 不过⻛的因素最终将会影响到⽐赛的进⾏。这个问题曾被提出与讨论在我的伙伴⺴站讨论区 Wizard of Vegas拉斯维 加斯巫师。
如果玩家在玩掷骰子游戏时下注超过赔率倍数,而庄家直到赌注赢或输才注意到,通常会发生什么情况?
我曾就此问题咨询过一位前拉斯维加斯赌桌游戏经理。他说,赔率投注超过允许的线注倍数的部分将按位置投注赔率支付。这个问题在我的同伴网站“拉斯维加斯巫师”的论坛上被提出并讨论过。
在NFL美式⾜球, 平均⽽⾔, ⼀队得分之后另⼀队也得分的机率是多少?
根据2000-2009年NFL美式⾜球的球季, 答案是57%.
假设有一场三人决斗,参与者有A、B和C。他们为了争夺一个女人而决斗至死。他们都是绅士,并且都同意以下规则。
- 三名参与者形成一个三角形。
- 每颗子弹只有一颗。
- A 先走,然后是 B,最后是 C。
- A 击中预定目标的概率是 10%。
- B 击中预定目标的概率为 60%。
- C 击中预定目标的概率为 90%。
- 没有发生意外枪击事件。
- 允许向空中射击(故意射偏)和射击自己,并且总是成功的。
- 如果任何一轮结束后仍有两到三名幸存者,则每人获得一颗新子弹。之后,他们将按照相同的顺序轮流射击,跳过任何已经死亡的玩家。
- 三位参与者都是完美的逻辑学家。
A 最初应该瞄准谁?他针对每个初始目标的生存概率是多少?
BBC 节目《相当有趣》讨论了这个谜题。向下滚动 100 行即可查看答案和解答。
1
2
3
4
5
6
7
8
9
10
11
12
十三
14
15
16
17
18
19
20
21
22
23
24
二十五
二十六
二十七
二十八
二十九
三十
31
三十二
33
三十四
三十五
三十六
三十七
三十八
三十九
40
41
四十二
43
四十四
45
46
四十七
四十八
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
以下是我根据每个初始目标计算出的 A 获胜的概率。如你所见,故意向空中射击可以最大化 A 的获胜概率。
真实赔率
| 战略 | 概率获胜 |
| 空气 | 13.887% |
| 一个 | 0.000% |
| B | 12.560% |
| C | 13.094% |
为了解答这个问题,我们用 Pr(X) 表示一轮之后 X 组(且仅剩 X 组)存活的概率。用 Pr(X*) 表示 X 组最终赢得该轮的概率,重复此过程直至游戏状态因有人被击中而发生变化。用 Pr(X**) 表示玩家 X 是唯一幸存者的概率。为了找到最终的概率,我们先来看看两人的状态。显然,双方都会向对方射击。
A 与 B
- Pr(A) = 0.1
- Pr(B) = 0.9×0.6 = 0.54
- Pr(AB) = 0.9×0.4 = 0.36
如果两人都幸存下来,那么他们将重复这个过程,直到只剩下一个幸存者。因此,最终幸存者的概率为:
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0.1/0.64 = 0.15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0.54/0.64 = 0.84375
A 与 C
- Pr(A) = 0.1
- Pr(C) = 0.9×0.9 = 0.81
- Pr(AC) = 0.9×0.1 = 0.09
如果两人都幸存下来,那么他们将重复这个过程,直到只剩下一个幸存者。因此,最终幸存者的概率为:
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0.1/0.91 = 0.10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0.81/0.91= 0.89010989
B 与 C
- Pr(B) = 0.6
- Pr(C) = 0.4×0.9 = 0.36
- Pr(BC) = 0.$×0.1 = 0.04
如果两人都幸存下来,那么他们将重复这个过程,直到只剩下一个幸存者。因此,最终幸存者的概率为:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0.6/.96 = 0.625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0.36/.96= 0.375
现在我们来分析三人的情况。我们先来考虑一下 A 瞄准 B 的情况。
三人游戏——A 瞄准 B
如果A击中B,那么C肯定能幸存,但可能击中A,也可能击不中。因此,击中B的两种可能结果是AC和C。如果A击中B未击中,那么B会瞄准威胁更大的C。如果B击中C,那么A和B都能幸存。如果B击中C未击中,那么C会瞄准威胁更大的B。如果C击中B未击中,那么A和C都能幸存。如果C击中B,那么A和C都能幸存。因此,可能的结果是C、AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0。
- Pr(C) = 0.1 × 0.9 = 0.09。这是通过 A 击中 B,然后 C 击中 A 实现的。
- Pr(AB) = 0.9 × 0.6 = 0.54。这是通过 A 击中 B,然后 B 击中 C 实现的。
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334。这可以通过两种方式实现。第一种是 A 命中 B,然后 C 未命中 A。第二种是 A 未命中 B,B 未命中 C,然后 C 命中 B。
- Pr(BC) = 0。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。这是通过三项全部缺失实现的。
按照与双人情况相同的逻辑,我们可以将每个结果除以 (1-Pr(ABC))=0.964 来找到每个状态的概率,假设游戏状态在回合之后确实发生了变化。
- Pr(C*) = 0.09/0.964 = 0.093361。
- Pr(AB*) = 0.54/0.964 = 0.560166。
- Pr(AC*) = 0.334/0.964 = 0.346473。
从双人对决的情况来看,如果是A和B,那么A获胜的概率为0.15625,B获胜的概率为0.84375。如果是A和C,那么A获胜的概率为0.109890,C获胜的概率为0.890110。
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600。A 可以通过两种方式获胜:(1) 进入 AB 状态,然后获胜;(2) 进入 AC 状态,然后获胜。
- Pr(B**) = 0.560166 × 0.84375 = 0.472640。如果B进入AB状态,则B获胜,B为胜者。
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760。C 可以通过 A 杀死 B,然后 C 在第一轮杀死 A 来获胜,或者通过进入状态 AC,然后 C 获胜。
因此,如果 A 的策略是首先瞄准 B,那么他成为唯一幸存者的概率是 12.56%。
三人游戏——A 瞄准 C
如果A击中C,那么B肯定会幸存,但可能会击中A,也可能不会。因此,击中C的两种可能结果是AB和B。如果A没有击中C,那么B会瞄准威胁更大的C。如果B击中C,那么A和B都会幸存。如果B没有击中C,那么C会瞄准威胁更大的B。如果C没有击中B,那么A和B都会幸存。如果C击中B,那么A和C都会幸存。因此,可能的结果是B、AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0.1 × 0.6 = 0.06。
- Pr(C) = 0。
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58。这可以通过两种方式实现。第一个是 A 击中 C,然后 B 击中 A。第二个是 A 击中 B,然后 B 击中 C。
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324。这是通过 A 缺失 C、B 缺失 C 以及 C 命中 B 实现的。
- Pr(BC) = 0。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。这是通过三项全部缺失实现的。
按照与双人情况相同的逻辑,我们可以将每个结果除以 (1-Pr(ABC))=0.964 来找到每个状态的概率,假设游戏状态在回合之后确实发生了变化。
- Pr(B*) = 0.06/0.964 = 0.062241。
- Pr(AB*) = 0.58/0.964 = 0.601660。
- Pr(AC*) = 0.324/0.964 = 0.336100。
按照与 A 针对 B 的情况的解决方案相同的逻辑:
- Pr(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943。
- Pr(B**) = 0.062241 + 0.601660 × 0.84375 = 0.569891。
- Pr(C**) = 0.336100 × 0.890110 = 0.299166。
因此,如果 A 的策略是首先瞄准 C,那么他成为唯一幸存者的概率是 13.09%。
三人 — A 故意失手
A故意射偏后,B会瞄准威胁更大的C。如果B击中C,A和B都会幸存。如果B射偏C,C会瞄准威胁更大的B。如果C射偏B,A和B都会幸存。如果C射偏B,A和C都会幸存。因此,可能的结果是AB、AC和ABC。
- Pr(A) = 0。
- Pr(B) = 0。
- Pr(C) = 0。
- Pr(AB) = 0.6。这是通过 B 击中 C 实现的。
- Pr(AC) = 0.4 × 0.9 = 0.36。这是通过 B 未命中 C,然后 C 命中 B 实现的。
- Pr(BC) = 0。
- Pr(ABC) = 0.4 × 0.1 = 0.04。这是通过全部三个缺失来实现的。
按照与双人情况相同的逻辑,我们可以将每个结果除以 (1-Pr(ABC))=0.96 来找到每个状态的概率,假设游戏状态在回合之后确实发生了变化。
- Pr(AB*) = 0.6/0.96 = 0.625。
- Pr(AC*) = 0.36/0.96 = 0.375。
按照与 A 针对 B 的情况的解决方案相同的逻辑:
- Pr(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865。
- Pr(B**) = 0.625 × 0.84375 = 0.527344。
- Pr(C**) = 0.375 × 0.890110 = 0.333791。
因此,如果 A 的策略是首先瞄准 C,那么他成为唯一幸存者的概率是 13.89%。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。


