请问巫师 #253
好问题。为了方便其他读者,以下是双人游戏中,这两手起手牌对抗随机牌的概率:
KJ 同花 vs. A-7 不同花
| 手 | 赢 | 失去 | 画 | 预期价值 |
钾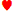 J J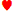 | 0.6148 | 0.3634 | 0.0218 | 0.2513 |
一个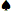 7 7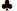 | 0.5717 | 0.3949 | 0.0334 | 0.1768 |
然而,根据我的双人德州扑克计算器,这两手牌互相面对的概率是:
A7 胜率 = 53.52%
KJ 胜率 = 46.10%
平局 = 0.39%
所以,在我的牌表中,KJ 同花的排名更高,但在对局中却不如 A7 异花。为什么?
答案很难解释。当两手牌互相对抗时,你必须考虑它们如何相互作用。例如,在起手牌强度表中,非同花AK仅略优于非同花AQ,预期值分别为0.3064和0.2886。然而,如果将它们互相对抗,AK会压倒AQ,如下所示:
AK 获胜率 = 71.72%
AQ 获胜 = 23.69%
平局 = 4.58%
在A7异花对阵KJ同花的比赛中,A比K和J高出一筹。KJ玩家获胜的最大机会是,他拿到了K或J,并且没有A出现。我计算出这种情况的概率只有37.73%。其余46.10%的KJ获胜概率来自更大的牌。
尽管 A7 对抗 KJ 很强,但它更容易被随机牌所压制。
也许这个比喻不太恰当,但它有点像石头剪刀布游戏。对于技艺娴熟的玩家来说,每次出手的力量等级应该大致相同。然而,如果一个玩家出布,另一个出剪刀,那么力量等级就毫无意义,剪刀会赢。
在拉斯维加斯的 Bighorn and Longhorn 赌场,他们允许在 21 点游戏中三张牌加倍。根据这条规则,我应该调整策略吗?
我的“拉斯维加斯巫师”网站的一位读者说,相对于庄家拿到软 17 点的标准多副牌策略,应该做出以下改变:
- 击中软 13 对抗 5 或 6
- 击中 2 张软 15 点对 4 点
- 命中 3,3 对 2
击中软牌的原因是,击中后你可能会得到更好的软加倍。根据此规则,击中3的价值更高,因为击中A可以算作一个好的3张加倍。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。
如果将一枚硬币抛 100 次,那么至少有一次连续出现 7 次正面的概率是多少?
我不知道这个问题是否有一个简单的、非递归的表达式来表达。但是,有一个简单的递归表达式来表达。
f(n)= pr(第一次抛反面的个数)×f(n-1) +
pr(第一次抛掷正面,第二次抛掷反面)×f(n-2) +
pr(前两次抛掷的正面,第三次抛掷的反面)×f(n-3) +
pr(前三次抛掷的正面,第三次抛掷的反面)×f(n-4) +
pr(前四次抛掷的正面,第四次抛掷的反面)×f(n-5) +
pr(前五次抛掷的正面,第五次抛掷的反面)×f(n-6) +
pr(前六次抛掷的正面,第六次抛掷的反面)×f(n-7) +
pr(前 7 次抛掷的正面次数) =
(1/2)×f(n-1)+
(1/2) 2 ×f(n-2)+
(1/2) 3 ×f(n-3)+
(1/2) 4 ×f(n-4)+
(1/2) 5 ×f(n-5)+
(1/2) 6 ×f(n-6)+
(1/2) 7 × f(n-7) +
(1/2) 7
在哪里:
f(n)=n次翻转内成功的概率。
pr(x)=x发生的概率。
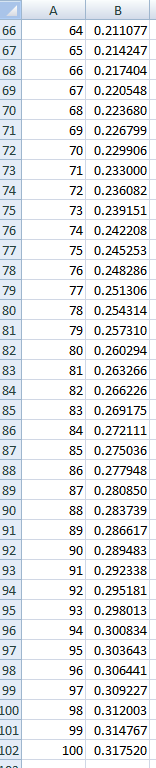
电子表格非常适合解决这类问题。在下面的电子表格截图中,我在单元格 B2 到 B8 中输入了概率 0,因为在 6 次或更少的抛掷次数内不可能连续出现 7 次正面。在单元格 B9 中,我输入了以下公式:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
然后我把它从单元格B10复制粘贴到单元格B102,相当于翻转100次。这个概率是0.317520。随机模拟证实了这一点。
 |  |
这篇文章最初发表后,Rick Percy 与我分享了他的矩阵代数解法。以下是我自己的解释。我假设读者已经了解矩阵代数的基础知识。
首先,在任何时候,弹球器可能处于八种状态:
p 1 = 成功的概率,假设从当前点开始你需要再掷出 7 个正面。
p 2 = 成功的概率,假设你需要从当前点开始再出现 6 个正面。
p 3 = 成功的概率,假设您需要从当前点开始再出现 5 个正面。
p 4 = 成功的概率,假设您需要从当前点开始再出现 4 个正面。
p 5 = 成功的概率,假设您需要从当前点开始再出现 3 个正面。
p 6 = 成功的概率,假设您需要从当前点开始再出现 2 个正面。
p 7 = 成功的概率,假设您需要从当前点开始再出现 1 个正面。
p 8 = 成功的概率,假设您不需要更多的正面 = 1。
我们将矩阵 S n定义为第 n次翻转后处于每个状态的概率。S 0表示第一次翻转之前的概率,其中有 100% 的概率处于状态 0。因此 S 0 =
| 1 0 0 0 0 0 0 0 |
令 T 为两次连续翻转的变换矩阵,即从 S n到 S n+1 ,其中 S n+1 = T × S n
- 如果您处于状态 1,那么在一次翻转之后,您有 0.5 的机会处于状态 2(正面),并且有 0.5 的机会保持在状态 1(反面)。
- 如果您处于状态 2,那么在一次翻转之后,您有 0.5 的机会处于状态 3(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 3,那么在一次翻转之后,您有 0.5 的机会处于状态 4(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 4,那么在一次翻转之后,您有 0.5 的机会处于状态 5(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 5,那么在一次翻转之后,您有 0.5 的机会处于状态 6(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 6,那么在一次翻转之后,您有 0.5 的机会处于状态 7(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 7,那么在一次翻转之后,您有 0.5 的机会处于状态 8(正面),并且有 0.5 的机会返回到状态 1(反面)。
- 如果您处于状态 8,那么您就取得了成功,并且将以 1.0 的概率保持在状态 8。
将所有这些放在转换矩阵 T = 的形式中
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
为了得到一次翻转后每个状态的概率...
(1) S1 = S0 ×T
翻转两次之后怎么样?
(2) S2 = S1 ×T
让我们用方程 (2) 代替方程 (1)...
(3) S2 = S0 ×T×T= S0 × T2
那么翻转 3 次之后呢?
(4) S3 = S2 ×T
将方程 (3) 代入方程 (4)...
(5) S3 = S0 × T2 ×T= S0 × T3
我们可以一直这样做,直到第 100 次翻转之后的状态......
S 100 = S 0 × T 100
那么,T 100是多少?在计算机出现之前,弄清楚这些数字一定非常困难。然而,借助 Excel 的 MMULT 函数,经过大量的复制粘贴,我们发现 T 100 =
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
右上角的项显示了翻转 100 次后处于状态 8 的概率,即 0.317520。
最近,托斯卡纳赌场推出了一项促销活动:如果你在30天内拿到30张黑杰克,就能赢得100美元的奖金。起初,最低下注金额是5美元,就能在卡上盖章。后来我听说最低下注金额提高到了15美元。我给赌场经理写了一封投诉信,信中写道:
如果这是真的,我只是想表达我对这个变化的失望。我从来没有机会利用这个促销活动,现在也怀疑自己是否还能利用。拿到30张黑杰克所需的时间(据说大约需要连续玩8个小时)似乎不合理,因为促销活动的奖金仍然只有100美元。
以下是我收到的回复:
回复您关于二十一点停牌促销活动的电子邮件,我不确定您是从哪里获得关于完成停牌卡需要多长时间的信息的。我们见过玩家在不到四个小时内就完成了这张卡。而且,您有三十天的时间来完成这张卡。我希望您理解,这并不是一项在这么短的时间内无法完成的任务。感谢您的来信。很高兴收到客户的反馈。希望您能尝试一下并赢取一些奖金!
四小时内拿到 30 张黑杰克的概率是多少?
根据我的游戏比较,二十一点玩家每小时大约玩70手牌。六副牌游戏中出现二十一点的概率是24*96/combin(312,2)=4.75%。我假设二十一点平局仍然会盖章。所以大约需要30/0.0475=632手牌才能填满牌,也就是9.02小时。
假设玩了280手牌,那么在4小时内完成牌局的概率是3万分之一,前提是每次只玩一手牌。我怀疑任何在4小时内达到目标的玩家,每次至少都玩了两手牌。
这个问题是在我的同伴网站Wizard of Vegas的论坛中提出并讨论的。


