骰宝附录

简介

这篇附录的⺫的是要推导出骰宝赌局中不同押注选项对于玩家的优势。为 了将事情简化, 我使⽤玩家的优势, 有别于赌场的优势, 因为这样从玩家的 ⽴场来想事情会⽐较容易些。玩家的优势总是负数的, 若要得到赌场的优 势, 只要将之乘以(-1)就好。玩家优势的通⽤公式是将所有可能的回报率乘 以它们个别的机率。注意丢掷三颗骰⼦总共有6X6X6=216种可能的排列组 合。

 

• 低:

  如果不算triple三颗同点的状况, 这个押注没有赌场优势。三颗同点在1点, 2点, 或3点时的机率为3/216. 总点数在3点到10点之间的机率为1/2, 或 108/216. 所以赢注的机率为108/216 - 3/216 = 105/216. 因此玩家的优势 为(105/216)*(+1) + (111/216)*(-1) = -6/216 =~-2.78%.

• ⾼: 参⻅Low低

   

• 特定点数:

  摇出0颗骰⼦特定点数的机率为 (5/6)^3 =125/216.
  摇出1颗骰⼦特定点数的机率为 3*(1/6)^1*(5/6)^2 = 75/216.
  摇出2颗骰⼦特定点数的机率为 3*(1/6)^2*(5/6)^1 = 15/216.
  摇出3颗骰⼦特定点数的机率为 (1/6)^3 = 1/216.因此玩家的优势为(125/216)*(-1) + (75/216)*(+1)+ (15/216)*(+2) + (1/216)*(+3) = - 17/216 =~-7.780%.

• 总点数4点:

  共有3种形式摇出4点: (1+1+2, 1+2+1, 2+1+1). 因此玩家的优势为 3/216*(+60) + (213/216)*(-1) = -33/216 =-15.278%.

• 总点数5点:

  共有6种形式摇出5点: (1+1+3, 1+3+1, 3+1+1, 1+2+2, 2+1+2, 2+2+1). 因 此玩家的优势为6/216*(+30) + (210/216)*(-1) =-30/216 = -13.889%.

• 总点数6点:

  共有10种形式摇出6点: (1+1+4, 1+4+1, 4+1+1, 1+2+3, 1+3+2, 2+1+3, 2+3+ 1,3+1+2, 3+2+1, 2+2+2). 因此玩家的优势为10/216*(+17) + (206/216)*(-1) = -36/216 =-16.667%.

• 总点数7点:

  共有15种形式摇出7点: (1+1+5, 1+5+1, 5+1+1, 1+2+4, 1+4+2, 2+1+4, 2+4+ 1,4+1+2, 4+2+1, 1+3+3, 3+1+3, 3+3+1, 2+2+3, 2+3+2, 3+2+2) . 因此玩家的优势为15/216*(+12) + (201/216)*(-1) =-21/216 = -9.722%.

• 总点数8点:

  共有21种形式摇出8点: (1-1-6 * 三种, 1-2-5 * 六种, 1-3-4 * 六种, 2-2-4 * 三 种, 2-3-3 *三种). 因此玩家的优势为21/216*(+8) + (195/216)*(-1) = -27/216 =-12.500%.

• 总点数9点:

  共有25种形式摇出9点: (1-2-6 * 六种, 1-3-5 * 六种, 1-4-4 * 三种, 2-2-5 * 三 种, 2-3-4 *六种, 3-3-3 * ⼀种). 因此玩家的优势为25/216*(+6) + (191/216)*(-1) =-41/216 = -18.982%.

• 总点数10点:

  共有27种形式摇出10点: (1-3-6 * 六种, 1-4-5 * 六种, 2-2-6 * 3 三种, 2-3-5 * 六种, 2-4- 4 * 三种, 3-3-4 * 三种). 因此玩家的优势为27/216*(+6) + (189/216)*(-1) =-27/216 = -12.500%.

• 总点数11点: 参⻅ 总点数10点

   

• 总点数12点: 参⻅ 总点数9点

   

• 总点数13点: 参⻅ 总点数8点

   

• 总点数14点: 参⻅ 总点数7点

   

• 总点数15点: 参⻅ 总点数6点

   

• 总点数16点: 参⻅ 总点数5点

   

• 总点数17点: 参⻅ 总点数4点

   

• ⼆数:

  让我们假设所选择的⼆个点数为1点和2点, 这1点和2点共有30总排列组合: 1-2-1 * 三种, 1-2-2 * 三种,1-2-3 * 六种, 1-2-4 * 六种, 1-2-5 * 六种, 1-2-6 * 六种. 因此玩家的优势为30/216*(+5) +(186/216) *(-1) = -36/216 = -16.667%.

• 特三:

  只有⼀种⽅式摇出Specific triplet特三的相同点数。因此玩家的优势为 1/216*(+180) + (215/216)*(-1) = -35/216 =-16.20%.

• 任三:

  有6种⽅式摇出Any triplet任三的相同点数。因此玩家的优势为 6/216*(+30) +(210/216)*(-1) = -30/216 = -13.889%.

• 双点对⼦

  让我们假设所选择的是1点的对⼦, 摇出2颗或3颗1点骰⼦的排列组合共有 16种: 1+1+1, 1+1+2 * 三种, 1+1+3 *三种, 1+1+4 * 三种, 1+1+5 * 三种, 1+1+6 * 三种. 因此玩家的优势为16/216*(+10) + (200/216)*(-1) = -72/216 = -18.52%.

---

以下为 n 颗骰⼦摇出总点数为 s 的公式, 摘⾃ Richard A. Epstein 所著的 The Theory of Gambling and Statistical Logic 赛局理论与统计逻辑, 公 式5-14.

 

 

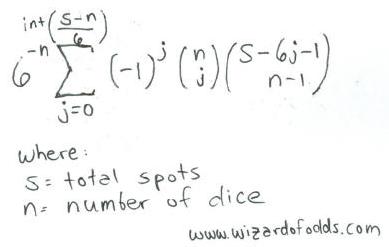
举例说明, 让我们以3颗骰⼦摇出点数11为例, 演算如下

int[(s-n)/6] = int[(11-3)/6] = int[1.33] = 1

其总和将是 6^-3 * [-1⁰*combin(3,0)*combin(11-6*0-1,3-1) + -1¹*combin(3,1)*combin(11-6*1-1,3-1) ] =
1/216 * [1*1*combin(10,2) + -1*3*combin(4,2)] =
1/216 * [1*1*45 + -1*3*6] =
1/216 * [45-18] = 27/216 = 12.5%

撰写者: Michael Shackleford