在这一页
押注妙⽅的真相
在这一页
简介
「betting systems押注妙⽅」不仅⽆法击败具有赌场优势的赌场游戏, 它 们甚⾄不会起到任何⼀点影响。轮盘的⼩球和骰⼦就是没有记忆, 每次 Roulette轮盘的旋转和Craps花旗骰的掷骰⼦与过去的所有事件都是独⽴ 的。在短期间内, 你可以⾃欺地以为某个押注妙⽅是可⾏的、因⽽冒险投 注很多却赢得很少。然⽽, ⻓期下来没有任何押注妙⽅是可以禁得起时间 的考验。你玩的时间愈⻓, 输掉⾦额相对于押注⾦额的⽐率、将愈加趋近 于那个游戏的期望值。
经营这个⺴站多年以来, 我收到过上以千计来⾃押注偏⽅信众们的e-mails 电邮, 他们的信念已超越了宗教的层次。然⽽, 在所有事情中, 愈是荒谬的 信仰、其信念坚持愈是顽固。数百年来赌徒们就不断寻求某种可⾏的押注 妙⽅, 然⽽赌场依然屹⽴不摇。
赌徒的谬论
最⼤的赌博神话观点就是, ⼀个最近都没发⽣的事件、由于迟迟未发⽣ 过、所以极可能就会发⽣。这就是所谓的「gambler's fallacy赌徒的谬 论」。上千个赌徒曾经设计出押注妙⽅, 尝试从最近出现的结果、以相反 的押注⽅式来引⽤这款赌徒的谬论。例如, 在轮盘赌桌等待出现三次红⾊ 之后、再押注在⿊⾊上⾯。⼩贩们叫卖「保证」快速发财的押注妙⽅, 最 终就是建⽴在这款赌徒的谬论之上。没有⼀种妙⽅是有⽤的, 如果你不相 信我的话, 这⾥有某些资料来源是说到关于这个主题的:
⼀种普遍的赌徒谬论称为「机会成熟论」(或「Monte Carlo fallacy蒙地 卡罗谬论」)错误地假设在⼀种游戏之中、每⼀回合的机会并不独⽴于其 他回合之外, 某⼀种连续结果必然会被另⼀种短缺的机率所平衡。⼲泛地 根据这种谬论, 于是赌徒们发明了⼀堆「systems妙⽅」; 赌场经营者乐于 ⿎励这种妙⽅的使⽤、因为赌徒忽视了机率与独⽴赌局回合的法则。 — Encyclopedia Britannica⼤英百科全书(查看「gambling博弈」条⺫)
没有押注妙⽅可以将⼀个低于公平的游戏转换成获利的事业... — 《Probability and Measure机率与测量》(第⼆版, 94⻚) by Patrick Billingsley
押注妙⽅「保证」的数字, 关于这种妙⽅的神话与谬误之扩散, 还有⽆数⼈ 们成群结党对于这种妙⽅的相信、传播、尊崇、保护、和宣誓, 押注妙⽅ 在赌博历史上建⽴起最古⽼的错觉。押注妙⽅的狂热者就像是永动机器拥 护者的精神上亲族们, 将他们的头颅抵挡在热⼒学第⼆定律之前。— 《The Theory of Gambling and Statistical Logic博弈与统计逻辑理论》 (53⻚) by Richard A. Epstein
Vegas Click 还有对于赌徒谬论的 ⼀个不错揭发.
Martingale加倍赌注
我每星期都会收到两⾄三封电邮, 问我关于输掉之后加倍赌注的押注妙⽅ 问题。这个⽅法通常是玩在even money⽀付等额注⾦的赌戏上, 例如轮 盘的红⾊/⿊⾊押注、或是花旗骰的过关/不过关押注, 称之为 「Martingale加倍赌注」。原理是你每次输掉之后就加倍赌注, 最终你总 会赢⼀局, 不仅回本了所有输掉的钱、还倒赢⼀个押注单位的⾦额。例如, 如果玩家从$1开始玩起、并且连输四局, 在第五局赢的话, 他在那四局总共 输掉$1+$2+$4+$8 = $15, 在第五局赢得$16, 于是输掉的钱被补偿回来、 他还获利$1. 问题是当你连输好⼏次、押注加倍再加倍很快就会耗光你的 赌本, 这可⽐你想像中要来得容易。
为了要证明这点, 我创造了⼀个程序来模拟两种押注⽅式, 「Martingale 加倍赌注」和「flat betting持平押注」两种⽅式, 并将之运⽤在花旗骰的 pass line过关线押注上(有49.29%赢的机率)。 「Martingale加倍赌 注」的押注者总是从押注$1开始玩起, 并且周期开始有$255的资⾦、⾜以 连输8局。 「flat betting持平押注」的押注者则每次只押注$1. 「Martingale加倍赌注」玩家将玩⾄100局、或是直到他⽆法负担押注⾦ 额为⽌, 在那种情况时他必须停⽌游戏、并且带⾛所剩余的钱。在他的第 100局若是输的话, 他将继续押注下去直到赢为⽌、或是直到⽆法负担下⼀ 笔押注赌⾦。 「flat betting持平押注」的玩家则会连玩100局相同的$1 押注。我将这两种⽅式重复实验1,000,000个周期、并且将结果制成图 表。以下显⽰的为结果:
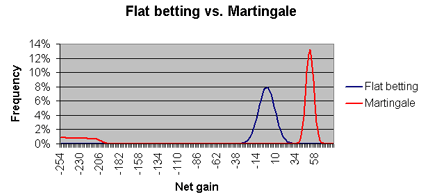
你可以看出, 「flat betting持平押注」的押注者有⼀个钟形曲线、最⾼峰 值位在输掉$1的位置, ⽽且不会偏离峰值太远。通常「Martingale加倍赌 注」的押注者会显⽰获利、由最右端的钟形曲线呈现, 其最⾼峰值位在$51 的位置; 然⽽, 在最左端我们也可⻅到那些因为输掉⼤量资⾦⽽⽆法负担押 注、最后离开的情况。许多加倍赌注的信徒们错误地相信, 有较多的赢局 ⾜以补偿较少的输局。
在这个实验⾥, 平均周期的持平押注者输掉的钱为$1.12, 但加倍押注者输 掉的钱则为$4.20. 在两种押注⽅式, 输掉⾦额相对于押注⾦额的⽐率都⾮ 常接近7/495, 那是花旗骰pass line过关线押注的赌场优势。这可不是巧 合。不管是⽤什么押注⽅式, ⻓期下来这个⽐率总是趋近于赌场优势。为 了证明这点, 考虑「Martingale加倍赌注」的玩家在花旗骰的过关线上只 想赢$1, 从$1开始下注, 并且有资本$2,047 ⾜以连输10局。以下列表显⽰ 所有可能结果、机率、期望押注值、还有回报率。
期望押注值expected bet为total bet押注总⾦额乘以机率。同理, 期望 回报率expected return为total return总回报率乘以机率。最后两个栏位 显⽰加倍赌注玩家的平均押注总⾦额为11.81172639, 平均输局为 0.16703451. 将平均输局除以平均押注⾦额得到0.01414141. 现在我们将7 除以495(过关线的赌场优势)、我们再次得到0.01414141! 这显⽰出 「Martingale加倍赌注」相较于「flat betting持平押注」并没有更好或 更糟、若是以期望输值expected loss相对于期望押注expected bet的 ⽐率来看的话。所有的押注妙⽅若是以这种⽅式相⽐, 则与持平赌注并⽆ 不同, 这也本该如此。换⾔之, 所有的押注妙⽅都同样是毫⽆价值的。
这⾥是我稍早之前主导的另⼀个实验, 证明和上⼀个实验相同的事。这个 是以三种不同的押注⽅式来测试轮盘赌戏。玩家1每次都持平押注$1, 他没 有使⽤押注妙⽅。玩家2从$1开始下注, 每次赢钱就再增加$1赌注, 若是遇 到输局则终⽌增加赌注、回归到最初押注$1的状态再从头开始。玩家3也 是从$1开始下注, 运⽤输局之后加倍赌注的策略, 也就是输掉赌注$x之后他 再押注$2x(Martingale加倍赌注), 若是遇到赢局则终⽌加倍赌注、回 归到最初押注$1的状态再从头开始。为了现实的考量, 我将玩家3的最⼤押 注⾦额限定为$200. 以下是该实验的结果:
玩家 1
- 总共下注的⾦额 = $1,000,000,000
- 平均下注的⾦额 = $1.00
- 总共输掉的⾦额 = $52,667,912
- 期待输掉的⾦额 = $52,667,912
- 输掉⾦额相对于总下注⾦额的⽐率 = 0.052668
玩家 2
- 总共下注的⾦额 = $1,899,943,349
- 平均下注的⾦额 = $1.90
- 总共输掉的⾦额 = $100,056,549
- 期待输掉的⾦额 = $99,997,018
- 输掉⾦额相对于总下注⾦额的⽐率 = 0.052663
玩家 3
- 总共下注的⾦额 = $5,744,751,450
- 平均下注的⾦额 = $5.74
- 总共输掉的⾦额 = $302,679,372
- 期待输掉的⾦额 = $302,355,340
- 输掉⾦额相对于总下注⾦额的⽐率 = 0.052688
你可以看出, 输掉⾦额相对于总下注⾦额的⽐率总是接近正常的赌场优势 1/19 ≈ 0.052632. 随着之前的输赢状况⽽改变押注⾦额的⽅式、和每次 总是押注同等⾦额的⽅式, 在⻓期的结果上并⽆不同。
第三个实验
「An Old Timer’s Guide to Beating the Craps Table 击败花旗骰赌桌的⽼ ⼿指南」曾是⼀种夸⼤保证将花旗骰赌桌变成你的收银机的⼀种押注妙 ⽅。我免费提供测试他的押注⽅式, 这⾥有 结果。
删除式押注妙⽅
尽管我⼀再警告别⽤押注妙⽅, 读者们还是不断来找我寻求建议。为了满 ⾜这些爱⽤押注妙⽅的⼈们, 我已对这种删除 式押注妙⽅ 做出全盘的解释与分析。
别浪费你的钱
⺴路上充斥着⼀堆贩售押注偏⽅的⼈, 允诺可以幸运地在游戏击败赌场。 现今那些贩售押注妙⽅的⼈, 就如同19世纪推销蛇油的江湖郎中。你⽆论 如何绝对不要浪费钱在任何赌博妙⽅上头。每次将之放到电脑做出模拟之 后, 肯定会失效、⽽且与「持平押注flat betting」显⽰出相同的输钱对押 注的⽐率。如果你问那贩卖妙⽅的⼈这个问题, 他可能会回答说:『现实 ⽣活中是没有⼈会在赌场试验⼏百万次的。 』你也可能听到他/她的押注 ⽅式在现实⽣活⾥可⾏、但⽤在电脑模拟则不⾏。这听起来倒也有趣, 专 业⼈⼠利⽤电脑来模拟现实⽣活的问题、⼏乎涵括各种领域的研究, 然⽽ ⼀提到押注⽅式的时候, 那贩售妙⽅的⼈将之运⽤上去时, 电脑分析就变得 「毫⽆价值且不可靠」起来。在任何的事件, 这种借⼝是谬误的; 电脑试验 数⼗亿次就是为了要证明⼀种押注⽅式是没有根据的。如果连在电脑上都 ⾏不通的话, 那在赌场也是没⽤的。
赌博妙⽅伴随着博弈的历史⼀样久远。没有任何妙⽅曾被证明过是可⾏ 的。根据内部消息, 我知道贩售押注妙⽅的⾏销者会从贩卖这种妙⽅到另 ⼀种妙⽅。这是⼀种肮脏的⾏业, 他们从别⼈那⾥盗取想法、并且总是尝 试改编旧的妙⽅使之看起来像是新的⼀般。
贩售妙⽅的⾏销者通常会允诺荒谬的优势。例如, 即令押注在even money⽀付等额注⾦只有1%的优势, 它也会毫⽆困难地⼀再叠加押注、 从$100等⽐级数押注达到$1,000,000的资⾦。我曾被要求证明这样的主 张, 所以写了⼀个电脑模拟, 以投掷硬币两⾯为基础, 有50.5%赢的机会。 整个过程中玩家押注他资⾦的1%, ⼀元以下四舍五⼊。然⽽, 如果赢局的 押注⾦额超过$1,000,000, 则玩家押注的⾦额只须够他达到$1,000,000就 好。此外, 我还跑了另⼀种模拟、其优势为2%、起始的资⾦为$1,000. 以 下为所有四种测试的结果。
$100 资⾦, 1% 优势
- 押注赢 = 7,182,811,698 (50.4999%)
- 押注输 = 7,040,599,544 (49.5001%)
- 玩家最先达到$1,000,000 = 79,438 (83.019%)
- 玩家最先输光破产 = 16,249 (16.981%)
- 达到$1,000,000的平均押注局数 = 174,972 (364.5 天, 每天8⼩时, 每⼩ 时押注60局)
$100 资⾦, 2% 优势
- 押注赢 = 7,027,117,205 (51.0000%)
- 押注输 = 6,751,539,769 (49.0000%)
- 玩家最先达到$1,000,000 = 215,702 (98.099%)
- 玩家最先输光破产 = 4,180 (1.901%)
- 达到$1,000,000的平均押注局数 = 63,775 (132.9 天, 每天8⼩时, 每⼩时 押注60局)
$1,000 资⾦, 1% 优势
- 押注赢 = 5,213,026,190 (50.4999%)
- 押注输 = 5,109,817,544 (49.5001%)
- 玩家最先达到$1,000,000 = 74,818 (99.0285%)
- 玩家最先输光破产 = 734 (0.9715%)
- 达到$1,000,000的平均押注局数 = 137,208 (285.8 天, 每天8⼩时, 每⼩ 时押注60局)
$1,000 资⾦, 2% 优势
- 押注赢 = 6,332,837,070 (50.9996%)
- 押注输 = 6,084,596,671 (49.0004%)
- 玩家最先达到$1,000,000 = 267,445 (99.9996%)
- 玩家最先输光破产 = 1 (0.0004%)
- 达到$1,000,000的平均押注局数 = 46,428 (96.7 天, 每天8⼩时, 每⼩时押 注60局)
这些模拟证明了只要⼀点点优势、像是1%那么⼩的数值, 还有⼀⼩笔$100 的资⾦, 你就可以⼀路慢慢赌到⼀百万元、等同于复利计算那样。但是你 从未听过这样的事真实发⽣过。这些赌博⽅式毕竟没起作⽤吗?!
这⾥有⼀些例⼦是贩卖押注妙⽅的销售者想要欺瞒利⽤数学不佳的⼈。⺴ 路上有好⼏百个像这样的⺴站, ⽽这个列表只是举例⽽已。这些⺴站常常 在⼀夜之间消失、或者突然跳到⾊情⺴站。如果这些连结并没有连到指定 的地⽅, 请让我知道。
还有, ⼩⼼外⾯许多其他贩卖迅速致富的赌博骗局, 他们宣称并⾮是押注妙 ⽅。这些⺴站通常会弄出⼀堆炫⺫的物理名词, 像是「Chaos混沌理论」 和「Fractals碎形⼏何」, 但⼜显⽰不出任何证据他们懂得这些字眼的涵 义。过去我曾经列出某些这样的⺴站, 但是收到愤怒的来信说道, 我不应该 批评我不懂的事。我个⼈觉得, 每⼀种宣称可以轻易击败赌场的⽅式那就 是诈骗, ⽽且我⽆须了解箇中的秘密到底为何。然⽽, 为了全然公平起⻅, 我只列举上述的押注妙⽅, 因为那些在数学上都已经被电脑模拟所破解过 了。如果有⼈真的找到轻易击败赌场的⽅式, 那为什么他们不因此⽽致富 呢?
概率巫师Wizard of Odds挑战
⼤约有六年的期间, 从1999年到2005年, 我提供$20,000给任何能够提出⼀ 种押注妙⽅、可以在⼗亿次赌局的电脑模拟中显⽰出获利。这⾥你可以找 到挑战的规则。然⽽, 在整段时期内, 我只有⼀位认 真的挑战者, 其他⼏百⼈都是在浪费我的时间, 假装有兴趣却从未进⾏到 底。所以在2005年⼀⽉我就将这项奖励给下架了。
我的版主, Michael Bluejay, 在他⾃⼰的⺴站 VegasClick.com 现在也提 供本质上相同的挑战。如果你接受他的挑战、并且赢了, 我将很乐意在本 ⺴站的⾸⻚宣告, 证明说专家错了。
第四个实验
在2004年⼗⽉, Daniel Rainsong接受了我的 挑战。 Rainsong先⽣很有 ⾃信他会赢, 他加倍我的$40,000赌注对抗他的$4,000. 虽然挑战的规则是 基于Craps花旗骰或Roulette轮盘, 我允许这个挑战可以基于Blackjack⼆ ⼗⼀点的规则、其赌场优势只有0.26%. ⼀种押注妙⽅可以这么⼩的赌场 优势、延展到1,028局押注, 如此去击败⼀款游戏? 请造访我的 挑战 专⻚查看详情。
请别再写信过来了
我对于那些建议玩家如何战胜负数期望值游戏的e-mails电邮已经不再回 信了。这样的电邮只要看到就会被删除。我在这⾥已经把这个主题该说的 都说过了, 还有在我的赌博常问问题集。
如果你真的想要讨论这个主题, 那我请你别在我的拉斯维 加斯的巫师 讨论区上发⾔, 取⽽代之到志趣相投的⼈们那⾥, 像是atJohn Patrick的⺴站讨论区(更新, 这个⺴站已经, 不意外地, 早就成为过去式 了)。